Planare Spirale
x (u) = f (c ∙ u) ∙ cos (u)
y (u) = f (c ∙ u) ∙ sin (u)
z (u) = u
(Ausnahme Helix)
3D Spirale
x (u) = f (c ∙ u) ∙ cos (u)
y (u) = f (c ∙ u) ∙ sin (u)
z (u) = c ∙ u
3D Spirale als Animation und Projektion der fertigen Spirale in die
x/y-Ebene
Rotationskörper
x (u, v) = f (u) ∙ cos (v)
y (u, v) = f (u) ∙ sin (v)
z (u, v) = u v ∈ [0, 2π]
x² + y² = [ f (z) ]²
Rotationskörper mit Randfunktion
Helicoid
x (u, v) = f (c ∙ u) ∙ cos (u) ∙ v
y (u, v) = f (c ∙ u) ∙ sin (u) ∙ v
z (u, v) = c ∙ u v ∈ [0, 1]
korrespondierendes Helicoid
3D Spirale als Rohr/Röhre
x (u, v) = (f (c ∙ u) + r ∙ cos (v)) ∙ cos (u)
y (u, v) = (f (c ∙ u) + r ∙ cos (v)) ∙ sin (u)
z (u, v) = r ∙ sin (v) + c ∙ u v ∈ [0, 2π]
max (-x+y+z, x-y+z, x+y-z, -x-y-z) = a
max (| x |, | y |, | z |) = a
| x | + | y | + | z | = a
max (| Φ∙x+y |, | Φ∙x-y |, | Φ∙y+z |, | Φ∙y-z |, | Φ∙z+x |, | Φ∙z-x |) = Φ²∙a
max (| x+y+z |, | -x+y+z |, | x-y+z |, | x+y-z |,
| Φ∙x+q∙y |, | Φ∙x-q∙y |,
| Φ∙y+q∙z |, |
Φ∙y-q∙z |, | Φ∙z+q∙x |, | Φ∙z-q∙x |) = ½∙Φ²∙a
max (2∙| x |, 2∙| y |, 2∙| z |, | x+y+z |, | -x+y+z |, | x-y+z |, | x+y-z |) = 2∙a
English speaking visitors: Please use a browser
with a translation function (Firefox, Chrome,...)
English speaking visitors: Please note
the information at the bottom of this page.
For English speaking visitors:
To my great regret, I have discovered that my Internet provider JIMDO has recently blocked the automated translation of web pages via Google Translate (it was implemented here as a push-button). Therefore, until further notice, English-speaking visitors are limited to using a browser with a translation function (Firefox, Chrome) or, for individual text passages, using Copy&Paste with a translation software…
Tipps zur Navigation:
- Auf dieser Webseite sind Links sowie Downloads im Text in gelb ohne Unterstrich dargestellt.
- Hinweise werden in orange und per Symbol angezeigt:
(optimale Navigation, beste Ansicht auf Smartphones, Zoomen für versteckte Details, Hinweis auf Audio-Objekt)
Typically, the translation is pretty close to an original translation so that the reader should be able to understand the ideas and contents.
Otherwise, you are welcome to contact me ...
For English speaking users:
You may use Google's Auto-Translation
for my web page by clicking on the following button:
Alaaf und Helau!!!
Frohe Ostern!
Frohe Ostern!
Die Bogenlänge L der Nielsen-Spirale kann direkt aus der Definition der Kurve abgeleitet werden. Von einem Startpunkt t1 bis zu einem Endpunkt t2 berechnet sich L aus dem Integral über den Betrag des Tangentenvektors 𝑟⃗ ′ (𝑡). Dieser wird durch Ableiten der Koordinatenfunktionen x(t) und y(t) nach t gebildet:
Der Betrag des Tangentenvektors ist
Die Bogenlänge L ergibt sich somit zu
Für die obigen Formen habe ich keine Parameterwerte angegeben. Der wirkliche Spaß besteht im eigenen Experimentieren mit oftmals überraschenden Ergebnissen; der interessierte Leser möge sich die Graphing Calculator 3D-Datei unten downloaden. Viele Formen mit Parameterwerten finden sich auch in der Patentschrift von Gielis auf den Seiten 39 - 73 [1].
Mit der Superformel lassen sich auch 3D-Objekte erzeugen (s. 3D Supershape).
In [2] versuchen die Verfasser durch verschiedene Funktionen modifizierte Gielis-Kurven an simulierte Daten anzupassen. Allerdings ist es bei einer gegebenen Figur nicht einfach, die Parameter zur Erzeugung dieser Figur zu bestimmen. Dies wurde mit zwei Methoden der globalen Optimierung (Simulated Annealing und Particle Swarm) versucht. Es ergab sich jedoch, dass diese Parameter nicht zuverlässig geschätzt werden konnten und keine eindeutigen Lösungen zustande kamen.
3D
Schneemann
aus Parameterflächen
"... und kam die goldene Herbsteszeit
und die Birnen leuchteten weit und breit..."
3D Kürbis als Parameterfläche
HAPPY HALLOWEEN
... Winterabend ...
Schneefall
... kleine Themenauswahl ...
Maus auf Objekt: Stop Slider
Klick auf Objekt: Sprung auf
relevante Seite
Klicken Sie auf ein Bild für eine größere Ansicht.
3D Kürbis als Parameterfläche
Ein-Schritt-Verfahren (one-step methods)
Zwei-Schritt-Verfahren (two-step methods)
"... und kam die goldene Herbsteszeit
und die Birnen leuchteten weit und breit..."
Erntezeit ...
3D Apfel als Parameterfläche
|
01.09.18 - Neue Galerie unter '3D Mathe / 3D Flächen / Parameterflächen'
28.08.18 - Bild-Icons auf einigen Seiten für einfachere mobile Navigation 07.07.18 - 'Spielwürfel' unter '3D Mathe / 3D Objekte' erweitert 16.06.18 - neu: 'Planetensystem' unter '3D Mathe' 09.05.18 - neu: 'Verfahrensvergleich' unter 'Numerische Verfahren/Nullstellen' 05.05.18 - Neue Beispiele beim Sekantenverfahren 29.04.18 - Alternative mit User Library unter 'Integral / Normalverteilung" 23.04.18 - neu: 'Sekantenverfahren' unter 'Numerische Verfahren/Nullstellen' 01.04.18 - Neue Beispiele beim Newton-Verfahren 24.03.18 - neu: 'Newton-Verfahren' unter 'Numerische Verfahren/Nullstellen' 18.03.18 - neu: 'Grundlagen' unter 'Numerische Verfahren/Nullstellen' 05.03.18 - neu: 'Iterationen' unter 'Numerische Verfahren' 02.01.18 - Neue Seitenstruktur |
|
26.08.17 Text
25.08.17 Text 24.08.17 Text 24.08.17 Text 24.08.17 Text 24.08.17 Text 24.08.17 Text |
Beispieldatei.gc3
Das ist ein Schlagwort
zum Überfahren mit der Maus.
Das Schlagwort ist ein zum Überfahren mit der Maus.
Das Schlagwort ist ein zum Überfahren mit der Maus.
Text
Wenn Sie hier im Text dieses Stichwort mit der Maus überfahren, öffnet sich ein Bild mit einem Erklärtext.
Die Planetenbahnen und die Bahn des Mondes um die Erde sind Ellipsen, wenn auch nahezu kreisförmig. Bei der Bahnberechnung für die Planeten und den Mond wurden außer der mittleren Umlaufzeit folgende Größen berücksichtigt (Werte bei [1]):
große Halbachse • Exzentrizität • Inklination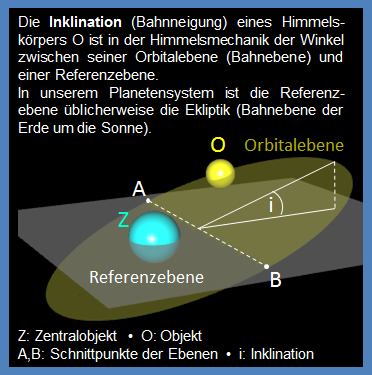
• Achsneigung (bei Erde und Saturn).
Die folgende Animation zeigt den Umlauf von Merkur (grau), Venus (orange) und Erde mit Mond um die Sonne für ein Jahr (hier: 2018). Schön zu sehen: durch die Neigung der Erdachse von 23.44° zur Ekliptik (Ebene der Umlaufbahn zur Sonne) entstehen die Jahreszeiten.
Die Planetenbahnen und die Bahn des Mondes um die Erde sind Ellipsen, wenn auch nahezu kreisförmig.
Bei der Bahnberechnung für die Planeten und den Mond wurden berücksichtigt (Werte bei [1]):
- große Halbachse
- Exzentrizität
-
Inklination
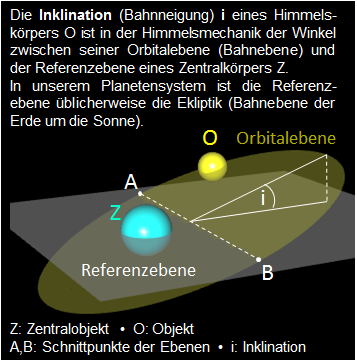
- Achsneigung (bei Erde und Saturn)
- mittlere Umlaufzeit.
Die folgende Animation zeigt den Umlauf von Merkur (grau), Venus (orange) und Erde mit Mond um die Sonne für ein Jahr (hier: 2018). Schön zu sehen: während die Erde die Sonne umläuft, bleibt die Neigung der Erdachse von 23.44° zur Ekliptik (Ebene der Umlaufbahn um die Sonne) im Raum (abgesehen von langperiodischen Effekten) fast unverändert . Dadurch ist von März bis September die Nordhalbkugel etwas mehr zur Sonne hin geneigt, von September bis März die Südhalbkugel. Im Jahreslauf ändern sich daher der Einfallswinkel der Sonnenstrahlen und die Dauer des lichten Tages, womit die Jahreszeiten entstehen.
Die Planetenbahnen und die Bahn des Mondes um die Erde sind Ellipsen, wenn auch nahezu kreisförmig. Bei der Bahnberechnung für die Planeten und den Mond wurden außer der mittleren Umlaufzeit folgende Größen berücksichtigt (Werte bei [1]):
große Halbachse • Exzentrizität • Inklination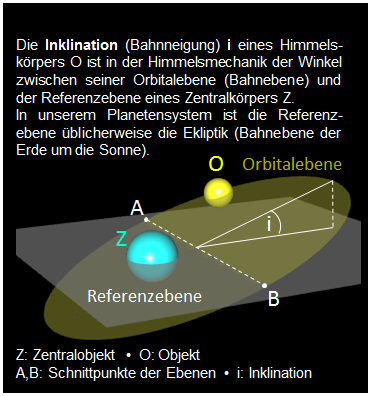
• Achsneigung
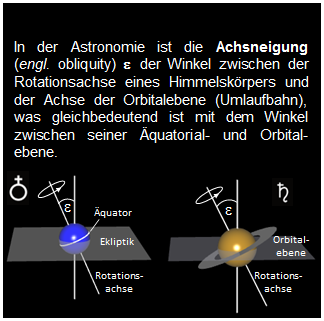(bei Erde und Saturn).
Die folgende Animation zeigt den Umlauf von Merkur (grau), Venus (orange) und Erde mit Mond um die Sonne für ein Jahr (hier: 2018). Schön zu sehen: durch die Neigung der Erdachse von 23.44° zur Ekliptik (Ebene der Umlaufbahn zur Sonne) entstehen die Jahreszeiten.
| Integrale | Integralanwendungen | |||||
| Numerische Integration | Doppelintegral | Fläche zwischen Funktionsgraphen | Flächenschwerpunkt zwischen Funktionsgraphen | Länge Funktionsgraph | Normalverteilung | |