Sekanten-Verfahren
Das Sekantenverfahren ist ein numerisches Verfahren zur näherungsweisen Berechnung der Nullstelle einer reellen stetigen Funktion f (x), d.h. der Lösung der reellen Gleichung f (x) =0.

Die Idee dieses Verfahrens ist es, die Funktion zwischen zwei Startpunkten (x0 | f(x0)) und (x1 | f(x1)) zu linearisieren, d.h. sie dort durch eine Sekante s zu ersetzen:
Der Schnittpunkt
x2 der Sekante mit der x-Achse wird dann als verbesserter Startwert für die Iteration verwendet; setzt man
s (x) = 0, ergibt sich
x2 zu

Nun wiederholt man den obigen Schritt mit den Punkten
(x1
| f(x1))
und (x2
| f(x2)),
usw.
Somit ergibt sich folgende Iterationsvorschrift:
Die Grafik rechts zeigt die ersten Iterationsschritte mit den vier Näherungslösungen x2, x3, x4 und x5.
Die obige Iterationsvorschrift lässt sich auch aus dem Newton-Verfahren herleiten, indem man dort die Ableitung durch den Differentialquotienten ersetzt:
(Anmerkung: Auch wenn durch vielfältige Publikationen der Eindruck erweckt wird, dass das Sekanten-Verfahren von Newtons Methode herrührt, indem es eine endliche Differenzenannäherung an die Ableitung verwendet, konnte Joanna M. Papakonstantinou im Rahmen ihrer Doktorarbeit A Historical Development of the (n+1)-point Secant Method den Ursprung der Sekantenmethode bis 1800 v. Chr. zurückverfolgen [1].)
Ein großer Vorteil des Sekantenverfahrens liegt darin, dass die Funktion nicht unbedingt in geschlossener Form angegeben sein muss, sondern ein funktionaler Zusammenhang (z.B. Messdaten) auch als Wertetabelle vorliegen kann.

Als Beispiel diene die folgende Grafik; hier wird der Einzugsbereich für die Nullstelle der diskreten Funktion f* ermittelt. Diese besteht aus 16 Wertepaaren (die orangene Linie dient nur als optische Führungslinie):
Das Verfahren liefert für Startwerte aus dem Intervall [0, 1.4] und maximal 100 Iterationen die Nullstelle mit einer Genauigkeit von 10-15; ab x = 1.5 divergiert es.
Konvergenzbetrachtungen

Das Sekantenverfahren divergiert grundsätzlich, falls die Funktion keine Nullstelle besitzt oder wenn in der Iterations-folge {xi} für zwei aufeinander folgende Näherungswerte xi und xi+1 deren Funktionswerte gleich sind, also falls f (xi) = f (xi+1) gilt.
Dies kann bei "unglücklicher" Wahl bereits für die ersten beiden Startwerte x0 und x1 passieren oder auch später, wie das Beispiel in der Grafik rechts zeigt. Hier wurden für die Funktion f (x) = x² die Startwerte x0 = 0.5 und x1 = - 1.5 gewählt, was dazu führt, dass die zweite Sekante parallel zur x-Achse verläuft und es dann im nächsten Schritt zu einer Division durch 0 kommt.
In der Literatur - und vornehmlich in Schulbüchern - wird empfohlen, die Startwerte x0 und x1 so zu wählen, dass f (x0) • f (x1) < 0 gilt, d.h. dass x0 und x1 unterschiedliche Vorzeichen haben und beide ungleich 0 sind.
Zwar bedeutet dies für eine stetige Funktion, dass sie dann im Intervall [x0, x1] mindestens eine Nullstelle besitzt, nicht aber, dass das Sekantenverfahren diese auch liefert.
Dazu betrachte man z.B. die Funktion f (x) =
x4 – x2 – 1 mit den Nullstellen bei
± 1.27201964951407…
Wählt man die Startwerte
x0 = -1.5 und
x1 =1 (s. folgende linke Grafik mit erster Sekante in blau und zweiter Sekante in grün), so divergiert das Verfahren. Die Sekanten werden zunehmend flacher, und die Werte der
Iterationsfolge {xi}
werden zunehmend größer (s. folgende rechte Grafik).
Lässt man z.B. x0 den Bereich von -2.3 bis -1.3 mit x1 = x0 + 1.3 durchlaufen (grüner Balken in folgender linker Grafik), so liegt in allen Intervallen [x0, x1] stets eine Nullstelle der Funktion, die das Sekantenverfahren aber nicht notwendigerweise findet.
Weiterhin ist es nicht unbedingt erforderlich, dass im Startintervall [x0, x1] auch eine Nullstelle liegt (vergleichbar mit dem Newton-Verfahren, wenn x0 "weit" von der zu ermittelnden Nullstelle entfernt liegt).
So können auch beim Sekantenverfahren "Sprünge" auftreten, d.h. die berechnete Nullstelle liegt ausserhalb des Startintervalls [x0, x1], wie dies in der folgenden rechten Grafik der Fall ist. Hier wurde das Intervall [-4, 4} mit dem Sekantenverfahren durchlaufen, wobei x1 = x0 + 10-13 galt. Im Bereich zwischen den Extremwerten von f divergiert das Verfahren.
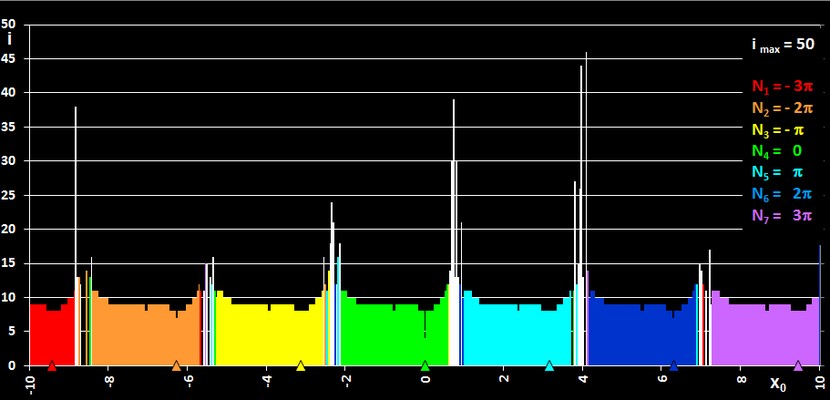
Als weiteres Beispiel betrachte man die Funktion f (x) = sin (x) mit ihren Nullstellen bei Vielfachen von π. In der folgenden linken Grafik durchläuft x0 den Bereich von -10-0.5 π bis 10-0.5 π (Auflösung: 500 Punkte in x-Richtung) mit x1 = x0 + 0.5 π - 10-15, so dass in allen [x0, x1] Intervallen stets eine Nullstelle von f liegt. Die vom Verfahren gelieferten Nullstellen sind farbig markiert; in y-Richtung sieht man, nach wie vielen Schritten die geforderte Genauigkeit von 10-15 erreicht wurde. Weiße Linien zeigen an, dass Nullstellen ausserhalb von [-10, 10] gefunden wurden; diese können recht weit entfernt sein: im berechneten Beispiel lagen die weitest entfernten Nullstellen bei -616 π und 13814 π. Schwarze Lücken bedeuten, dass das Verfahren mit der vorgegebenen maximalen Schrittzahl divergiert.
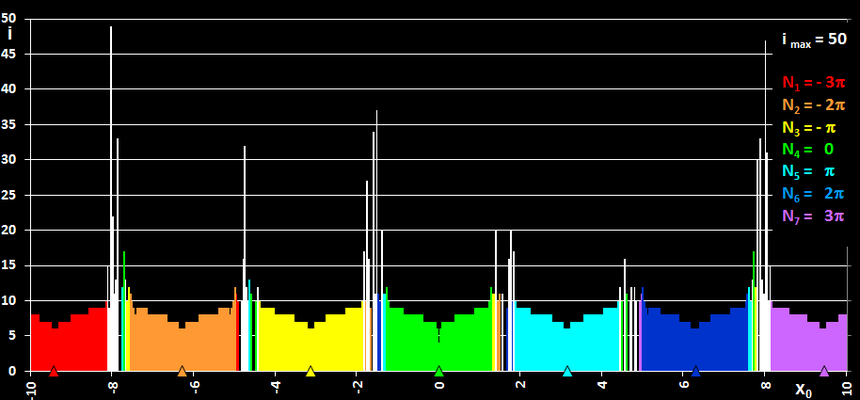
Wählt man die Länge des Startintervalls sehr klein, z.B.10-14 (dies entspricht fast dem Newton-Verfahren) und durchläuft das Intervall [-10, 10], so ergibt sich die folgende rechte Grafik. Die weitest entfernten Nullstellen liegen bei -4871 π und 1450293 π.
Aufgrund der Verwandtschaft zum Newton-Verfahren zeigt das Sekantenverfahrens bis auf Oszillation ähnliche Ergebnisse bezüglich des Konvergenzverhaltens.
Man kann zeigen [2], dass das Sekantenverfahren im Falle einer einfachen Nullstelle superlinear mit der Konstanten 1.618 (dies entspricht dem Verhältnis ϕ des goldenen Schnittes) konvergiert, d.h. die Zahl der korrekten Stellen des Näherungswertes erhöht sich pro Durchgang um mehr als eins.
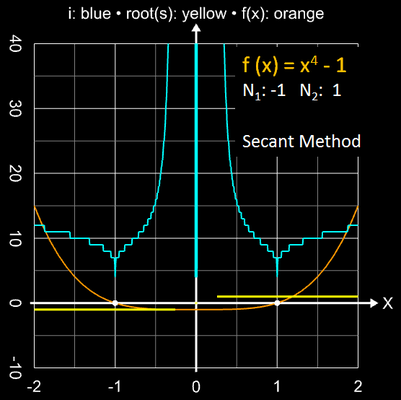
Da der Differenzenquotient nur eine Näherung für die Ableitung ist, ist die Konvergenz im Vergleich zum quadratisch konvergergierenden Newton-Verfahren entsprechend geringer. Die folgende Bildsequenz zeigt den Einzugsbereich mit den jeweils erforderlichen Iterationsschritten für eine Genauigkiet von 10-15 für die Funktionen x2-1, x3-1 und x4-1 mit ihren einfachen Nullstellen.
Das Verfahren verliert deutlich an Genauigkeit und Konvergenzgeschwindigkeit, wenn die Ableitung an der Nullstelle den Wert 0 hat. Insbesondere bei Polynomen entspricht dies einer mehrfachen Nullstelle.
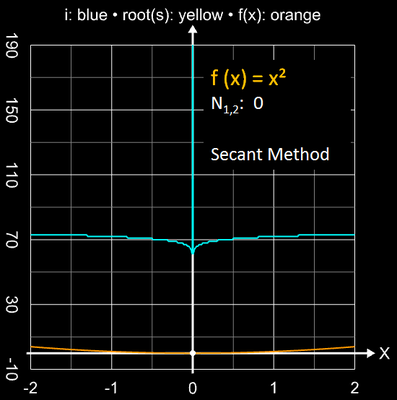
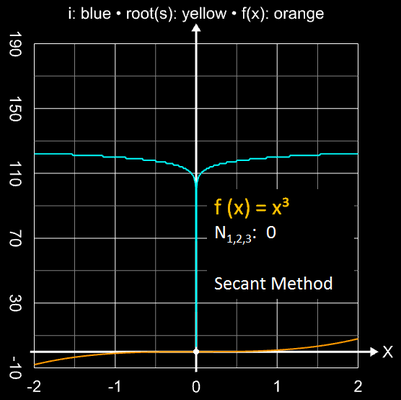
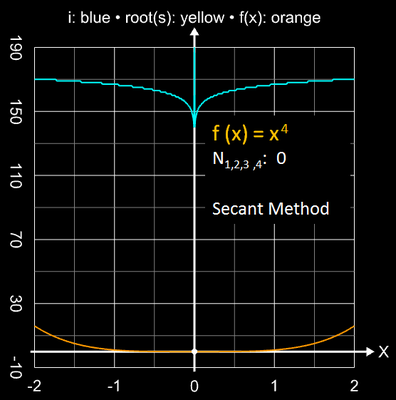
Die folgende Bildsequenz zeigt dies für die Funktionen x2, x3 und x4 bei einer geforderten Genauigkeit von 10-15.
___________________________
Eine Besonderheit beim Sekantenverfahren ist die Tatsache, dass bei der numerischen Berechnung Zähler und Nenner des Quotienten
mit zunehmender Annäherung an die Nullstelle ξ in den Bereich der auf dem Rechner / Software kleinsten darstellbaren Zahl geraten und der Quotient durch Auslöschung von Ziffern dann in die Form "0 / 0" übergeht. Während das Verfahren selbst die Abschätzung für die Nullstelle immer weiter verbessern könnte, wird in der tatsächlichen Berechnung dieser Gewinn in der Nähe der Nullstelle durch zunehmende Rundungsfehler überkompensiert. Dadurch lässt sich auf Rechnern mit endlicher Stellenzahl prinzipiell mit dem Sekantenverfahren nicht die Genauigkeit des Newtonschen Verfahrens erreichen.
___________________________
Vorteile und Nachteile des Verfahrens sowie weitere Beispiele finden Sie unter Verfahrensvergleich.
Quellenverweise
[1] Joanna M.
Papakonstantinou, A Historical Development of the (n+1)-point Secant Method
(2006)
[2] S. Funken, D. Lebiedz, K. Urban, Numerik II, S. 13
Download