Newton-Verfahren

Das Newton-Verfahren ist ein mathematisches Standardverfahren zur numerischen Lösung nichtlinearer Gleichungen. Im Falle einer Gleichung mit einer Variablen lassen sich für eine gegebene stetig differenzierbare Funktion f Näherungswerte zu Lösungen der Gleichung f (x) = 0 finden, was gleichbedeutend damit ist, Näherungen für die Nullstelle(n) der Funktion zu bestimmen.
Auf der Basis des Verfahrens, das Sir Isaac Newton (1643 - 1721) bereits im Zeitraum 1664 - 1671 aufstellte, sind inzwischen vielfältige Modifikationen entwickelt worden (s. Diverse Verfahren), hauptsächlich mit dem Ziel, die Konvergenzordnung (s. Iterative Verfahren zur Bestimmung von Nullstellen) des Verfahrens zu erhöhen und/oder bei der Iteration auf die Ableitung oder höhere Ableitungen der Funktion verzichten zu können.
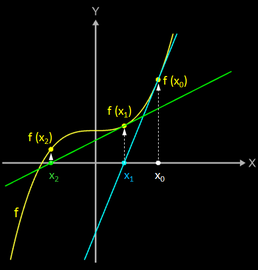
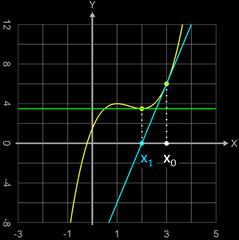
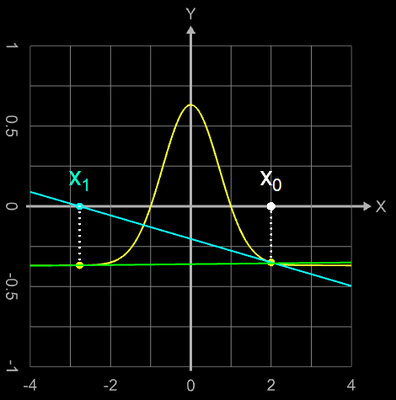
Die Idee des Newton-Verfahrens ist es, die Funktion in einem Ausgangspunkt (x0 | f(x0)) zu linearisieren, d.h. sie dort durch eine Tangente zu ersetzen.
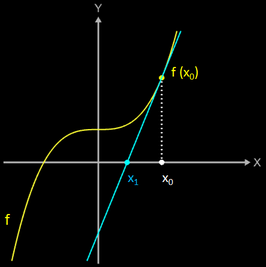
Man wählt eine Stelle x0
in der Nähe der gesuchten Nullstelle und legt an dieser Stelle eine Tangente an den Funktionsgraph (blau in Grafik). Die Tangente schneidet die x-Achse an der Stelle
x1;
diese liegt nun näher an der gesuchten Nullstelle.
Um die Stelle x1 zu bestimmen, gehen wir von der Steigung der Tangente im Punkt (x0 | f (x0)) aus; diese ist laut Definition der Steigung im Punkt eines Funktionsgraphen gleich dem Wert der Ableitung an der Stelle x0: f ' (x0).
Andererseits ergibt sich die Steigung der Tangente auch durch das Steigungsdreieck mit der Senkrechten f (x0) und der Waagerechten x0 - x1. Somit gilt:
Führt man den zuvor beschriebenen Schritt nun für die Stelle x1 aus, so ergibt sich die Stelle x2:
Wendet man diese Konstruktion mehrfach an (s. folgende Grafik und Animation für die nächsten Schritte)., so erhält man aus einer ersten Stelle x0 eine unendliche Folge von Stellen gemäß
Diese Iterationsvorschrift wird als Newton-Verfahren bezeichnet.
Diese Iteration erfolgt, bis eine hinreichende Genauigkeit erzielt wird, d.h. dass sich die Xi genügend nah der Nullstelle ξ angenähert hat. Als Abbruchkriterium hierfür verwendet man üblicherweise
|f (Xi)| < ε oder |xi+1 – xi| < ε.
Als Beispiel soll die Nullstelle der Funktion f (x) = 0.1 x³ - 0.8 ermittelt werden. Wie man leicht nachvollziehen kann, liegt diese bei ξ = 2, denn 0.1 • 8 - 0.8 = 0.
Mit der Wahl x0 = 1 als Startwert ergibt sich folgende Iterationssequenz (berechnet mit Graphing Calculator 3D und High-Precision-Bibliothek Apfloat mit 32 eingestellten Nachkommastellen):
Anmerkung zur Konvergenz/Genauigkeit:
Mit einer vorgewählten Nachkommastellenzahl von 300 wird bereits als 11. Iterationsschritt "2" angezeigt, da nach dem Dezimalkomma mehr als 200 Nullen folgen; bei eingestellten 400
Nachkommastellen wird bereits im nächsten Schritt die "2" angezeigt.)
Eine Graphing Calculator 3D-Datei für das Newton-Verfahren finden Sie unten im Download-Bereich.
Wahl des Startwertes beim Newton-Verfahren
Tatsächlich ist die Wahl des Startwerts x0 beim Newton-Verfahren nicht ganz unproblematisch; es können die folgenden Fälle A. bis C. entstehen.
A. Konvergenz
Bei günstiger Wahl des Startwertes, d.h. der Startwert liegt "hinreichend nah" bei der gesuchten Nullstelle, besitzt das Newton-Verfahren eine quadratischer Konvergenzordnung (q=2) , d.h. die Zahl der korrekten Dezimalstellen verdoppelt sich nahezu in jedem Schritt (einen Beweis hierzu findet man bei [1]). Die Effizienz (s. Iterative Verfahren zur Bestimmung von Nullstellen) beträgt CE = 1.414.
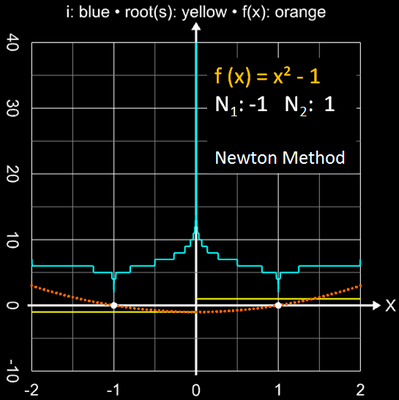
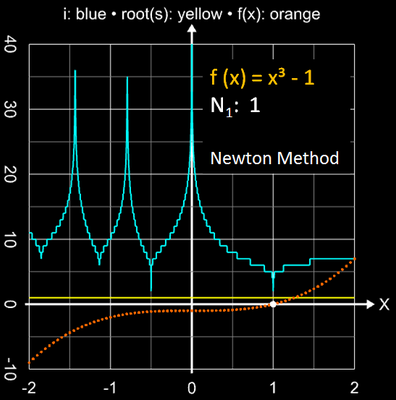
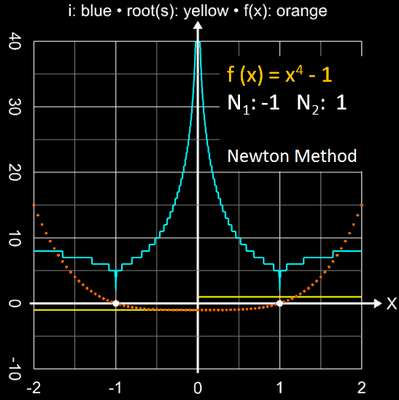
Die folgende Bildsequenz zeigt den Einzugsbereich mit den jeweils erforderlichen Iterationsschritten für eine Genauigkiet von 10-15 für die Funktionen x2-1, x3-1 und x4-1 mit ihren einfachen Nullstellen.
Wählt man den Startwert in der Nähe eines Extremwertes der Funktion oder handelt es sich bei der gesuchten Nullstelle um eine mehrfache Nullstelle, so erhöht sich die Anzahl der Iterationsschritte zum Erreichen der geforderten Genauigkeit deutlich. Im Falle einer mehrfachen Nullstelle beträgt die Konvergenzordnung dann nur noch q = 1 (lineare Konvergenz).
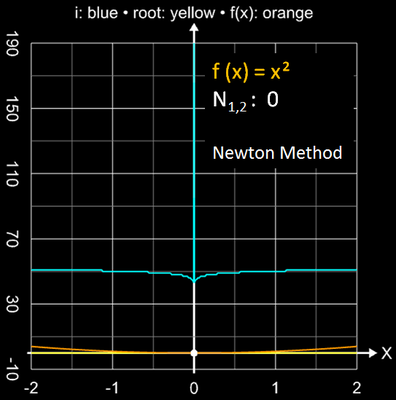
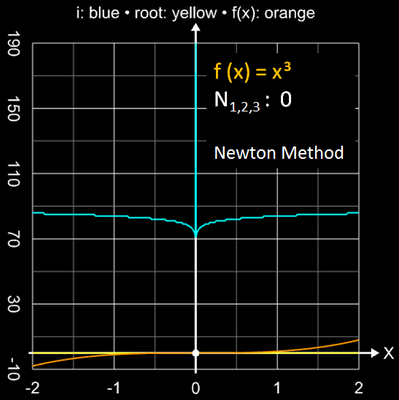
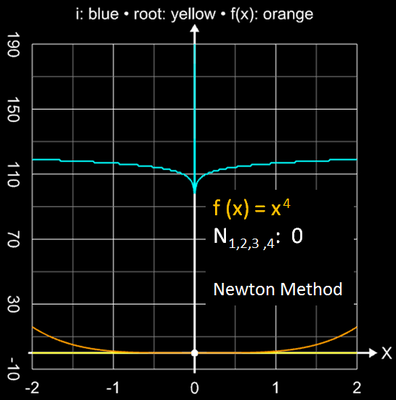
Als Beispiel dafür zeigt die folgende Bildsequenz die Einzugsbereiche mit den jeweils erforderlichen Iterationsschritten für eine Genauigkeit von 10-15 für die Funktionen x2, x3 und x4 .
Eine von E. Schröder weiter entwickelte Variante des Newton-Verfahrens zeigt auch im Falle mehrfacher Nullstellen eine quadratische Konvergenzordnung (s. Schröder-Verfahren).
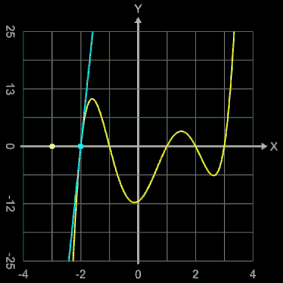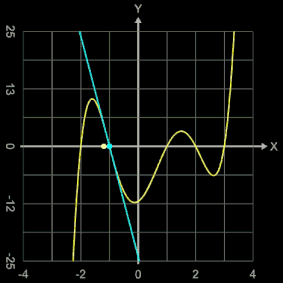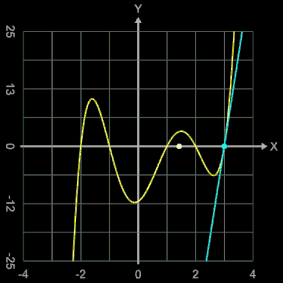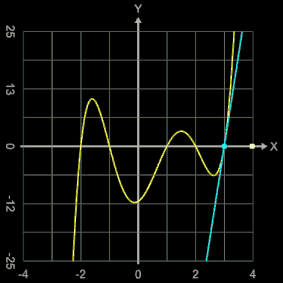
Als weiteres Beispiel sollen mit dem Newton-Verfahren die Nullstellen der Funktion
f (x) = (x + 2) (x + 1) (x - 1) (x - 2) (x - 3)
= x5 - 3x4 - 5x3 + 15x2 + 4x - 12
bestimmt werden; diese liegen, wie man unmittelbar an der Schreibweise des Funktionsterms mit Linearfaktoren erkennen kann, bei -2, -1, 1, 2 und 3.
Die Ableitung lautet f ' (x) = 5x4 - 12x3 - 15x2 + 30x + 4.
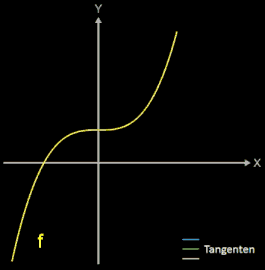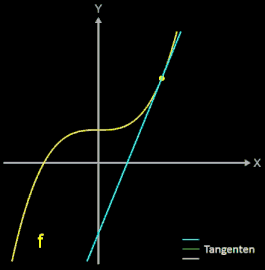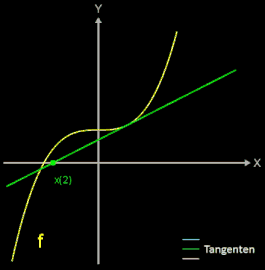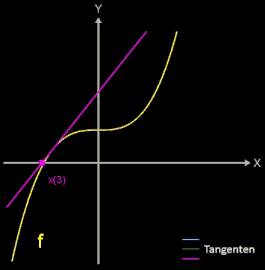
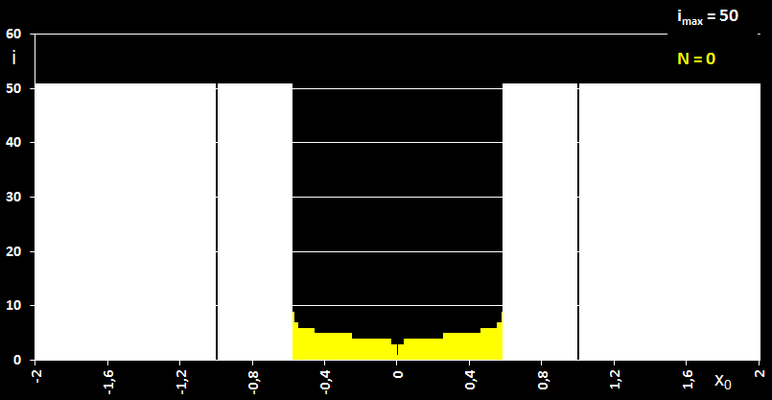
Animiert man den Startwert x0 über dem Intervall [-4, 4], so beobachtet man, dass die gefundenen Nullstellen nicht in der Reihenfolge -2, -1, ..., 3 auftreten - was man vielleicht erwarten würde - sondern dass es zu Sprüngen kommt (vgl. Grafik rechts mit der gefundenen Nullstelle und der dortigen Tangente).
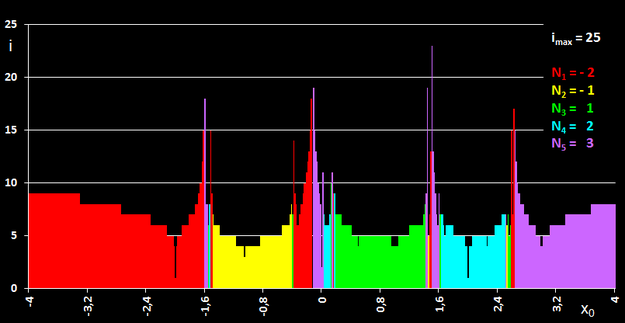
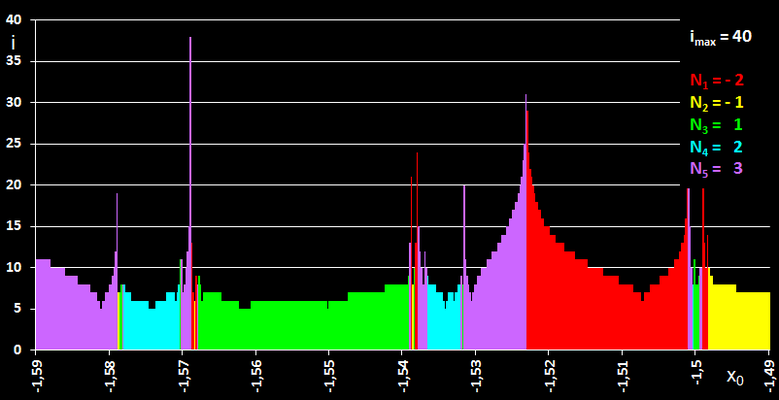
Die folgende Grafik zeigt dies genauer. Dort wurde das Intervall [-4, 4] in 500 Punkte aufgeteilt und für jeden Punkt als Startwert ermittelt
- nach wie vielen Schritten i die Iteration abbricht (y-Achse) und
- welche der fünf Nullstellen N1 bis N5 für den jeweiligen Startwert gefunden wurde.
Als Abbruchbedingung wurde eine Genauigkeit für die zu ermittelnde Nullstelle von 10-12 gewählt.
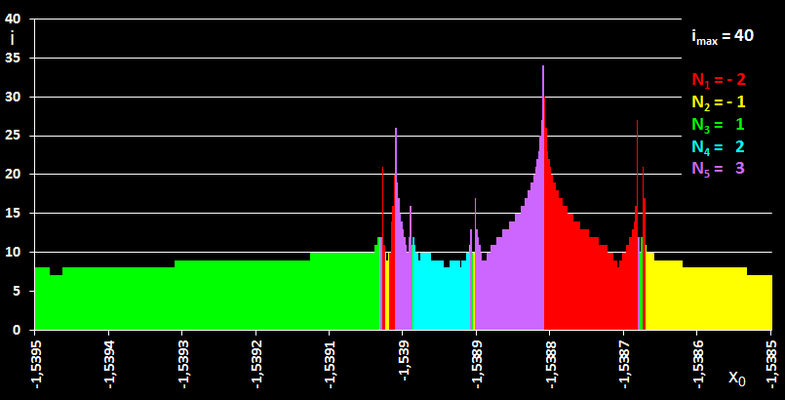
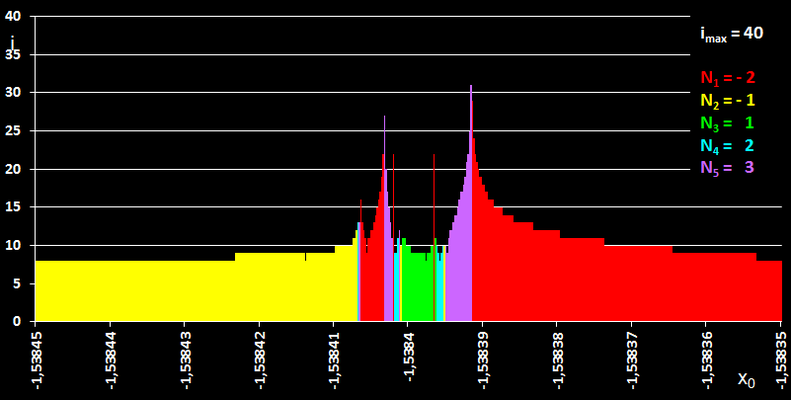
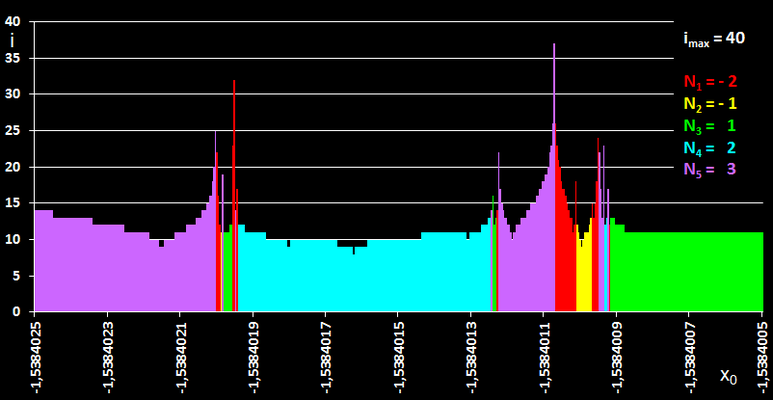
Zoomt man in ein Teilintervall hinein, in dem viele "Sprünge" stattfinden, wie z.B. in [-1.59, -1.49], so stellt man fest, dass es auch dort wieder Teilintervalle gibt, in denen die Iteration alle Nullstellen von f liefert (s. folgende Bildsequenz). Diesen Vorgang könnte man theoretisch unendlich oft fortsetzen - hier offenbart sich der fraktale (im Sinne von "vielfältig gebrochen") Charakter der Newton-Iteration.
B. Oszillationen
Es können Oszillationen auftreten, d.h. die Folge { xi } ist periodisch.
Dazu betrachte man z.B. die Funktion f (x) = x³ - 2 x + 2. Ihre Nullstelle liegt bei -1,76929265423863 ...
Wählt man
als Startwert x0 = 0, so oszilliert die Folge
{
xi } zwischen 0 und 1 (s. folgende Grafik links).
Dieser Zyklus ist stabil, er bildet einen Attraktor (ein Zustand, auf den sich ein dynamisches System hinbewegt und der nicht mehr verflassen wird) der Newton-Iteration, d.h. um beide Punkte gibt es Umgebungen, so dass Startpunkte aus diesen Umgebungen gegen den Zyklus konvergieren und somit mit geradem Index den Punkt 0 und mit ungeradem Index den Punkt 1 als Grenzwert der Teilfolge haben.
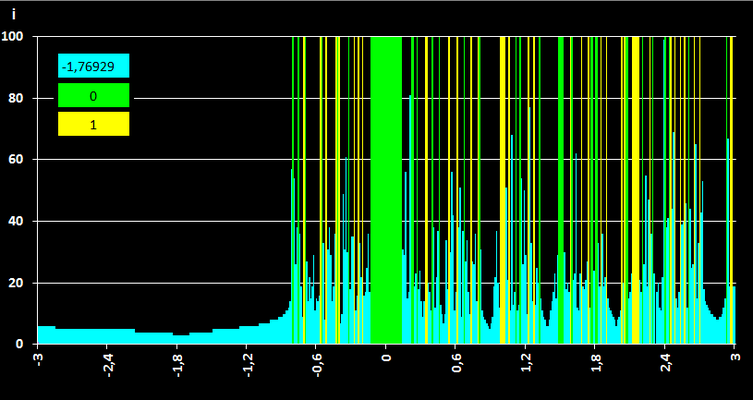
In der folgenden rechten Grafik wurde das Intervall [-3, 3] in 500 Punkte aufgeteilt und für jeden Punkt als Startwert ermittelt, ob die Iteration konvergiert (cyan) oder den Wert 0 (grün) oder 1 (gelb) einnimmt.
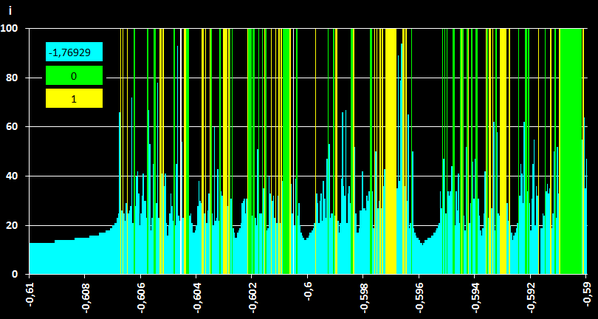
Während das Verfahren für Startwerte bis ca. - 0.75 stets konvergiert, treten für größere Startwerte vielfache Oszillationen auf. Zoomt man mit der Auflösung von 500 Punkten in einen cyan-farbenen Bereich z.B. bei [-0.61, -0.59] rein, so zeigt sich, dass es auch dort für viele Startwerte aus diesem Intervall zu Oszillationen kommt - es liegt ein fraktales Verhalten vor:
Als weiteres Beispiel für eine Oszillation betrachte man die Funktion f (x) = x³ - 4.5 x² + 6x + 1.5.
Sie hat eine Nullstelle bei x = -0,21401459124939...
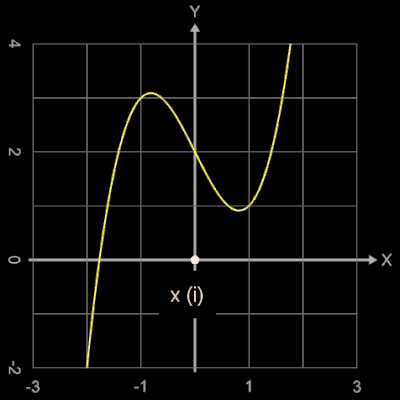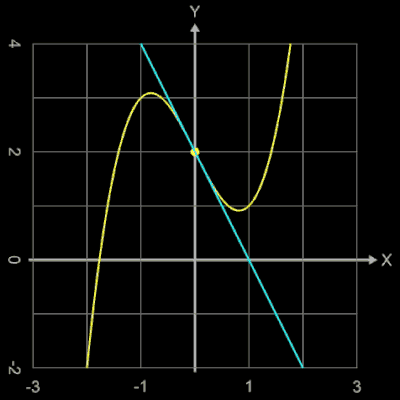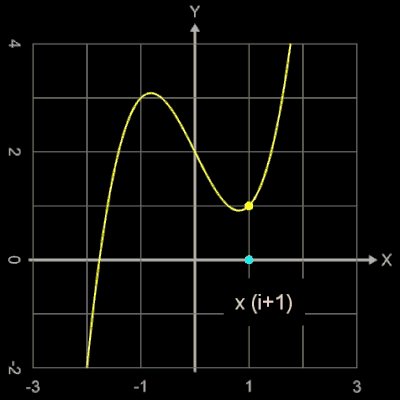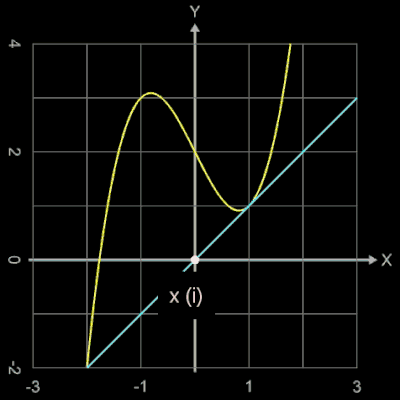
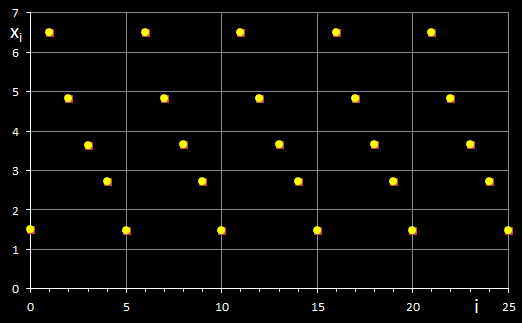
Wählt man als Startwert z.B. x0 = 1.5, so entsteht eine periodisch auftretende Folge von 5 Werten. In der Grafik rechts kann man dies verfolgen; dort markiert der weiße Punkt die Stelle xi und der cyanfarbene Punkt die Stelle xi+1 mit der zugehörigen Tangente.
Die entstehende Folge { xi } bis i = 25 ist in der folgenden linken Grafik dargestellt.
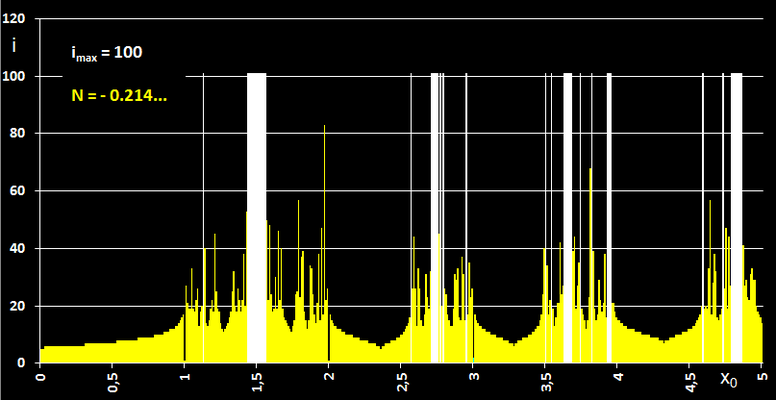
Die folgende rechte Grafik zeigt für Startwerte aus dem Intervall
[0, 5] an, ob für den jeweiligen Startwert die Folge
{
xi } gegen die Nullstelle konvergiert (gelb) oder ob eine Oszillation auftritt (weiß).
Außerdem sieht man, dass für x0 =1, 2, 3 Divergenz (s.u.) auftritt (schwarze Lücke).
Zoomt man in einen Bereich hinein, in dem Oszillationen auftreten, so offenbart sich auch hier die fraktale Struktur der Newton-Iteration.
C. Divergenz
Das Newton-Verfahren divergiert grundsätzlich, falls die Funktion f keine Nullstelle im Reellen hat, wie z.B. bei der Funktion f (x) = x² + 1.
Das Verfahren divergiert stets, falls beim Startwert x0 oder bei einem Wert xi der Iterationsfolge ein relatives Extremum oder ein Terassenpunkt liegt, da in diesem Fall die Tangente die Steigung 0 hat und somit die x-Achse nicht schneidet.
So divergiert das Verfahren z.B. für die obige Funktion f (x) = x³ - 4.5 x² + 6x + 1.5 für
x0 = 1 und
x0 = 2, da die Funktion dort relative Extrema besitzt. Aber auch für
x0 = 3 divergiert das Verfahren bereits im nächsten Schritt, da
x1 = 2 ist und dort ein Extremwert (Tiefpunkt) vorliegt (s. folgende linke Grafik).
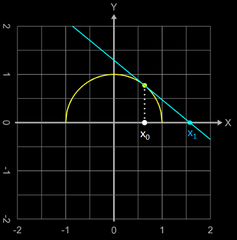
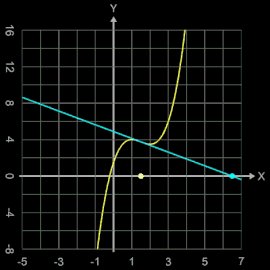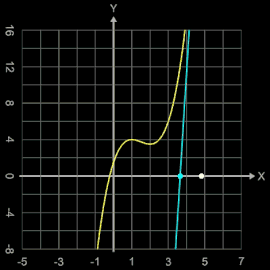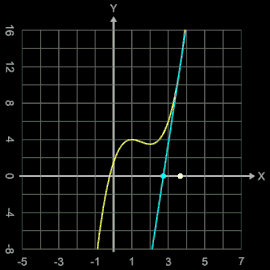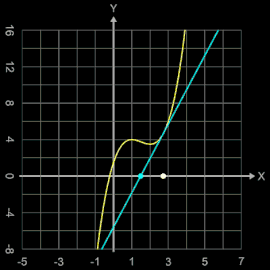
Das Newton-Verfahren versagt auch, falls die Ableitung an der Nullstelle nicht definiert ist und die Tangente zu einem Schnittpunkt mit der x-Achse führt, die außerhalb des Definitionsbereichs liegt, wie z.B. bei der Funktion
mit dem Definitionsbereich [-1, 1] und den Nullstellen {-1, 1} (s. folgende Grafik rechts).
___________________________
Als weiteres Beispiel für Divergenz betrachte man die Funktion
.
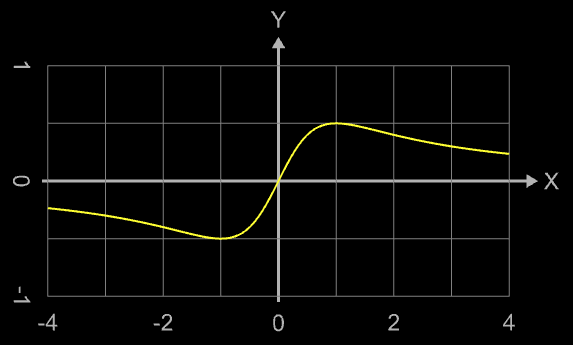
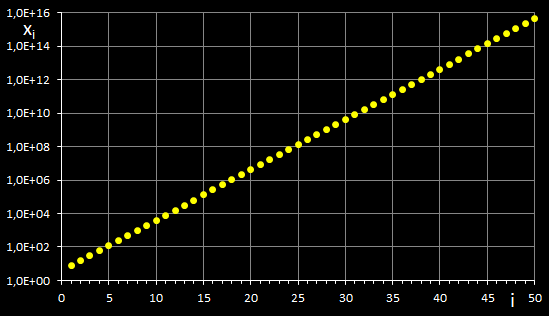
Sie hat eine Nullstelle bei x = 0 und relative Extrema bei x = -1 und x = 1 (s. folgende linke Grafik). Es lässt sich zeigen, dass für Startwerte aus
die Folge { xi } gegen die Nullstelle konvergiert. Für Startwerte außerhalb dieses Intervalls entfernen sich die Glieder xi der Folge immer mehr vom Startwert und der Wert | xi | nimmt schnell sehr große Werte an (s. folgende mittlere Grafik). Die rechte Grafik zeigt den Einzugsbereich für Konvergenz (gelb) und Divergenz (weiß).
___________________________
Divergenz mit einem sehr schnellen Anwachsen der xi gegen ±∞ tritt bei Anwendung des Newton-Verfahrens mit der Funktion f (x) = e-x² - e-1 (gelb in folgender linker Grafik) auf; sie hat die Nullstellen - 1 und 1.
Wählt man z.B. x0 = 2, so ist bereits bei x1 = -2.771... die Tangente (blau in folgender linker Grafik) nahezu parallel zur x-Achse. Die Werte der Iteration sind
x0 = 2
x1 = -2.771...
x2 = 140.798...
x3 = - ∞ (d.h. kleiner als 10-307: kleinste Zahl mit der Standardbibliothek von GC3D oder EXCEL).
Die folgende rechte Grafik zeigt die Einzugsbereiche des Verfahrens für das Intervall [-2, 2] mit 1000 Punkten und einer geforderten Genauigkeit von 10-15 für die Nullstellen; die Lücken zeigen Bereiche an, bei denen die Werte für x0 schon nach wenigen Schritten jenseits des darstellbaren Zahlenbereiches des Rechners liegen, mithin das Verfahren divergiert.
___________________________
Ein weiteres Beispiel für eine Newton-Iteration mit Divergenz und beliebig weitem Entfernen vom Startpunkt x0 liefert die Funktion f (x) = sin (x) mit ihren Nullstellen bei allen ganzzahligen Vielfachen von π.
Die Iteration divergiert bei allen Vielfachen von π/2, da die Funktion dort Extremwerte besitzt.
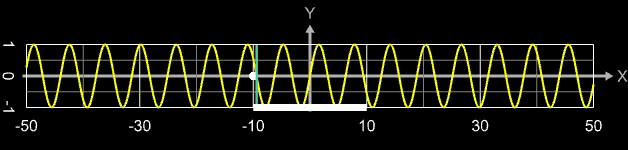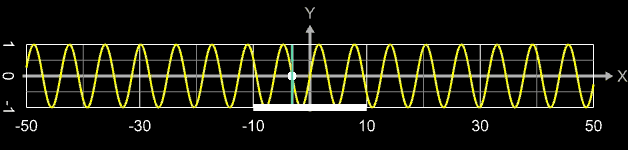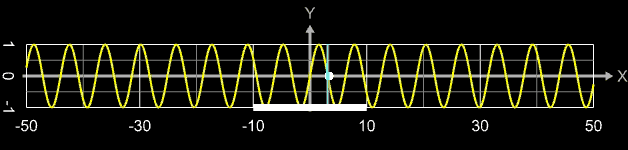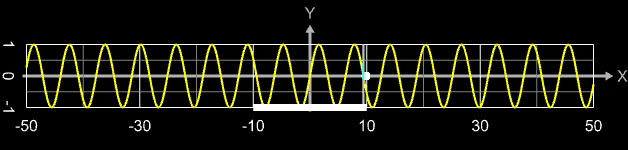
Im Bereich um die Extremwerte tritt "Springen" bei der Folge der gefundenen Nullstellen auf, d.h. diese liegen deutlich entfernt vom Startwert x0. In der folgenden Animation durchläuft x0 (weißer Punkt) das Intervall [-10, 10] (weißer Balken); die für den jeweiligen Startwert gefundene Nullstelle ist als blauer Strich markiert. Man erkennt, dass zwar die Nullstellen -3π, -2π, ..., 2π, 3π in diesem Intervall gefunden werden, aber auch Sprünge zu weiter entfernten Nullstellen auftreten (tatsächlich treten sogar noch viel mehr und weitere Sprünge auf, die aber auf Grund der Abtastrate beim Erzeugen der Animated-GIF-Grafik nicht angezeigt werden).
Dies ist in der Grafik rechts genauer zu sehen. Hier wurde das x-Intervall [-10, 10] in 1000 Punkte aufgeteilt. Mit jedem Punkt als Startwert x0 wurde eine Newton-Iteration durchgeführt und ermittelt, gegen welche Nullstelle k ("k-te" Nullstelle bedeutet, dass diese bei k • π liegt) die Iteration konvergiert (gelb).
Weiterhin zeigt die Grafik, wie viele Schritte i jeweils nötig sind, um die Genauigkeit von 10-15 zu erreichen (blau).
Man erkennt deutlich (Bild zoomen), dass für Startwerte in kleinen Umgebungen um die Nullstellen (weiße Punkte) das Verfahren gegen diese konvergiert (waagerechte gelbe Linien mit k = -3, -2, ..., 2, 3).
Es gibt jedoch Bereiche, bei denen die berechneten Nullstellen recht weit vom Startwert x0 entfernt sind.
Zoomt man in einen solchen Bereich hinein, so erkennt man, dass es dort weitere Unterbereiche gibt, bei denen die berechneten Nullstellen "beliebig" hin und her springen.
Dies soll im folgenden näher betrachtet werden ...
Die Iterationsvorschrift für f (x) = sin (x) lautet
Wählt man nun
x0 so, dass tan (x) =
π ist,
d.h.
x0 = arctan (π)
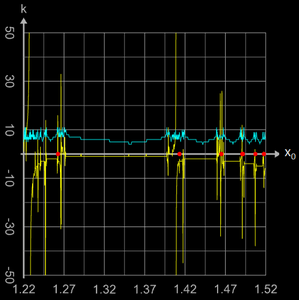
= 1.26262725567891... (in der Grafik erster roter Punkt von links), so gilt:
x1 = x0 – tan (x0) = x0 – π
x2 = x1 – tan (x1) = x0
– π – tan (x0 – π)
= x0 – π – tan (x0)
= x0 – 2 π
xi = x0 – i π
Dies bedeutet - zumindest in der theoretischen Betrachtung - dass die Glieder der Folge {xi} mit jedem Iterationsschritt i stets um ein weiteres π abnehmen und gegen - ∞ streben und somit die Folge für x0 = arctan (π) divergiert.
In der Rechenpraxis jedoch ist das Verfahren wegen der internen Rechengenauigkeit und Rundungsfehlern nicht stabil.
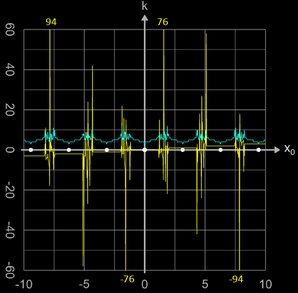
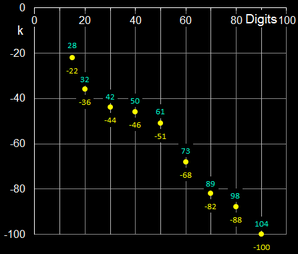
Die nebenstehende Grafik zeigt das Verhalten des Verfahrens für x0 = arctan (π) bei einer geforderten Genauigkeit von 10-15 und einer internen Rechengenauigkeit (Digits) bis zu 90 Nachkommastellen. Die Folge {xi} divergiert nicht, sondern "konvergiert" gegen weit entfernte k-te Nullstellen (gelbe Zahlen), wobei die blauen Zahlen die Anzahl der Iterationen angeben.
Auf die gleiche Weise wie oben lässt sich zeigen, dass ebenfalls Divergenz vorliegt, wenn für
x0 die Werte
arctan (2π) = 1.412965...,
arctan (3π) = 1.465088...,
arctan (4π) = 1.491386... etc. gewählt werden (rote Punkte in der vorigen Grafik).
Auf Grund der Periodizität der Winkelfuntionen treten solche Stellen aber auch auf für alle unendlich vielen Kombinationen von k und n aus {..., -3, -2, -1, 0, 1, 2, 3, ...} mit arctan (k•π) + n•π.
___________________________
Weitere Betrachtungen / Beweise zur Konvergenz / Divergenz sowie Beispiele für
das Newton-Verfahren findet man auf der deutschen
[2] und der
englischen Wikipedia-Seite [3] sowie unter Verfahrensvergleich.
Quellenverweise
[1] http://mathworld.wolfram.com/NewtonsMethod.html
Download