Komplexe Folgen und Reihen

Auf dieser Seite wird für komplexe Folgen a_n = ( z_n ) _n∈ℕ und Reihen ∑z_n _n_∈ℕ deren Konvergenzverhalten betrachtet, d.h. es wird mit Hilfe von EXCEL in grafischen Animationen dargestellt, auf welche Weise im Falle der Konvergenz sich für n→∞ die Folgeglieder bzw. Teilsummen dem Grenzwert nähern.

Komplexe Folgen

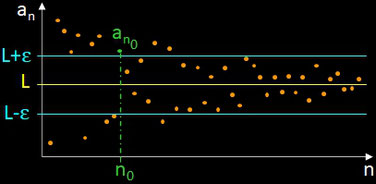
Bei reellen konvergenten Folgen streben mit größer werdendem Index n die Folgeglieder entweder monoton dem Grenzwert entgegen oder sie springen in immer kleiner werdenden Abständen um den Grenzwert hin und her. Für eine reelle Folge ( a_n ) _n∈ℕ mit dem Grenzwert L gilt:

Trägt man in einem x/y-Diagramm den Wert der Folgenglieder a_n über dem Index n auf (s. folgende Grafik), so bedeutet die Definition, dass zu jedem auch noch so kleinen ε > 0 ein Index n₀ existiert, ab dem dann alle folgenden Glieder ("alle bis auf endlich viele" in einem ε-Streifen um den Grenzwert L liegen.

Im Allgemeinen lässt sich ohne Mühe und Modifikation ein Großteil der Begriffe, Sätze und Methoden (Regeln zum Grenzwert, Cauchy-Charakterisierung, etc.) für reelle Folgen und Reihen auf komplexe Folgen und Reihen übertragen. Unterschiede ergeben sich nur durch die zweidimensionale Struktur und die fehlende Ordnung von ℂ. So gilt analog zum reellen Fall für eine komplexe Folge ( z_n ) _n∈ℕ :

Trägt man die Folgenglieder z_n in der Gauß'schen Zahlenebene auf (s. folgende Grafik), so bedeutet die Definition, dass zu jedem auch noch so kleinen ε > 0 ein Index n₀ existiert, ab dem dann für jedes folgende Glied z_n>n0 der euklidische Abstand zum Grenzwert L kleiner ist als ε, wobei es keine Rolle spielt, aus welcher Richtung sich die z_n dem Grenzwert annähern. Gleichbedeutend ist dies damit, dass in jedem noch so kleinen Kreis mit Radius ε > 0 um L alle bis auf endlich viele Glieder der Folge liegen.

Für die Diagramme / Animationen der Folgen gelten die folgenden Darstellungen / Einfärbungen:

• : Startwert z für die Folge

• : Glied der Reihe mit – Hilfslinien

• : a_N (Realteil: x-Achse, Imaginärteil: y-Achse)

( zⁿ ) _n∈ℕ0

Ein Beispiel einer konvergenten, komplexen Folge ist die geometrische Folge ( zⁿ ) _n∈ℕ0. Für ihre Konvergenz gilt:

Die Folge konvergiert also genau dann gegen 0, falls z in der offenen Kreisscheibe mit dem Radius 1 und dem Mittelpunkt (0 | 0) liegt oder falls z = 1 gilt.

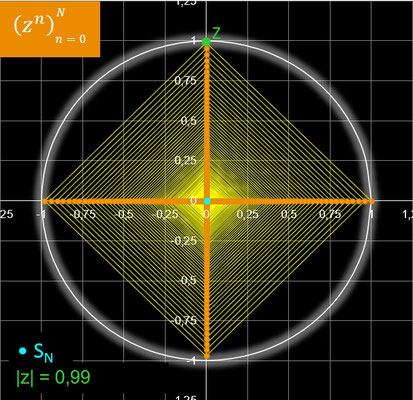
Als Beispiel zeigen die folgenden beiden Animationen, wie für einen Startwert z die Glieder a_n der Folge mit n = 0, ..., 100 = N dem Grenzwert 0 entgegen streben. Durch die Hilfslinien (Geraden) zwischen je zwei aufeinander folgenden Glieder a_n und a_n+1 entsteht ein Polygonzug, beginnend bei a₀ und endend bei a_N, wodurch sich die Entwicklung der Werte mit wachsendem n besser nachvollziehen lässt.

In der nebenstehenden Animation bewegt sich z aus dem Inneren der Kreisscheibe ( |z| < 1 ) auf den Rand des Konvergenzkreises ( |z| = 1 ) zu und verlässt diesen ( |z| > 1 ).

Für jeden Wert von z werden N = 500 Glieder der Folge berechnet.

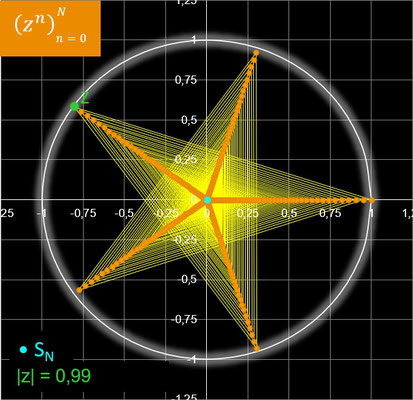
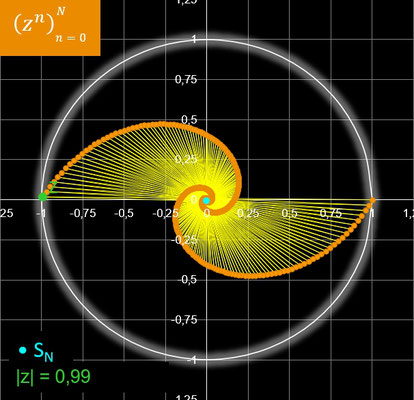
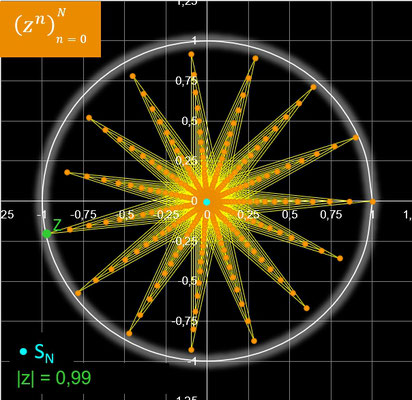
In der nebenstehenden Animation wandert z in Schritten von Δ φ auf einem Kreis entlang, dessen Radius r_z mit 0.99 etwas kleiner als 1 ist und somit Konvergenz vorliegt.

Für jeden Wert von z werden N = 500 Glieder der Folge berechnet. Für Δ φ wurde π / 180 = 1° gewählt.

Außer den vielfältigen "mäandernden Spiralen" ergeben sich für einige Werte von z auf den ersten Blick verblüffende Polygonzüge, von denen einige in der folgenden Galerie dargestellt sind. Durch Anklicken einer Grafik wird diese vergrößert, und der Wert für z bzw. der zugehörige Winkel φ wird angezeigt.

Folge (z^n), r=0.99, phi=144°, 5 "Speichen"

Folge (z^n), r=0.99, phi=160°, 9 "Speichen"

Folge (z^n), r=0.99, phi=192°, 15 "Speichen"

Folge (z^n), r=0.99, phi=206°, 7 "Flügel"

Folge (z^n), r=0.99, phi=340°, 18 "Speichen"

Komplexe Reihen

Sei nun a₀, a₁, a₂, ... eine Folge reeller oder komplexer Zahlen. Die Summe S_N

bezeichnet man als die N-te Partialsumme der a_n, die Folge ( s_N ) der Partialsummen nennt man eine unendliche Reihe und schreibt sie auch in der Form

Die Reihe heißt konvergent (bzw. divergent), falls die Folge der Partialsummen ( S_N ) konvergent (bzw. divergent) ist. Im wesentlichen gelten für komplexe Reihen die oben für komplexe Folgen gemachten Aussagen zu Regeln, Methoden und Grenzwerten sowie einige weitere. Diese findet der interessierte Leser z.B. in einer recht kompakten Darstellung mit Beispielen bei [1].

Im folgenden liegt der Fokus mittels Animationen vielmehr auf der Darstellung, wie sich für einen Startwert z die N Partialsummen einer unendlichen Reihe im Falle der Konvergenz dem Grenzwert der Reihe nähern.

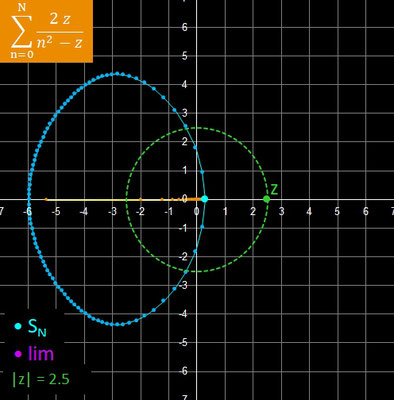
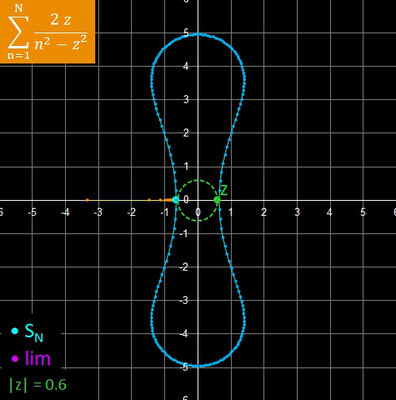
Hierbei wandert z - so nicht anders angegeben - in Schritten von Δ φ auf einem Kreis mit Radius r_z entlang, wobei r_z sehr nah am Konvergenzradius r des Konvergenzkreises (weiß mit Schattierung) der jeweiligen Reihe liegt. Jeweils zwei aufeinander folgende Glieder s_n und s_n+1 der Reihe (orangene Punkte) sind durch Strecken verbunden, um den Weg der Glieder hin zur N-ten Partialsumme (blauer Punkt) deutlicher zu machen.

Für die Diagramme / Animationen der Reihen gelten die folgenden Darstellungen / Einfärbungen:

• : Startwert z für die Reihe

• : Glied der Reihe mit – Hilfslinien

• : s_N (Realteil: x-Achse, Imaginärteil: y-Achse)

– : echte Grenzwerte für den Verlauf von z

• : N-te Partialsumme s_N für den Verlauf von z mit – Hilfslinien

Summiert man die Glieder der oben auf der Seite betrachteten geometrischen Folge ( zⁿ ) _n∈ℕ0, so erhält man die geometrische Reihe. Sie zeigt folgendes Konvergenzverhalten:

Animation:

r_z = 0.9 N = 200 Δ φ = 2 π / 180 = 2°

Animation:

r_Z = 0,99 N = 200 Δ φ = 2 π / 180 = 2°

Erhöht man für r_z =0.99 (s. obere rechte Animation) die Anzahl N der berechneten Partialsummen z.B. auf N = 500, so liegen die berechneten Werte der Summe s_N schon jeweils deutlich näher an den Grenzwerten (s. Grafik rechts).

r_Z = 0.99 N = 500 Δ φ = 2 π / 180 = 2°

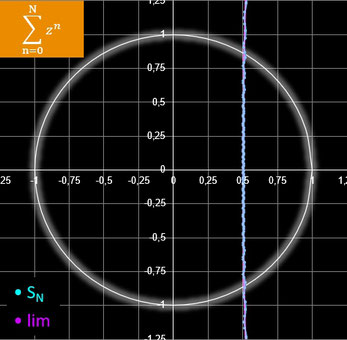
Animation:

r_z = 1.5 N = 20 Δ φ = 2 π / 180 = 2°

Animation:

r_Z = 1.007 N = 500 Δ φ = 2 π / 180 = 2°

Dies ist die Lambert-Reihe [3] mit dem Grenzwert

Animation:

r_z = 0.8

N = 500

Δ φ = 2 π / 180 = 2°

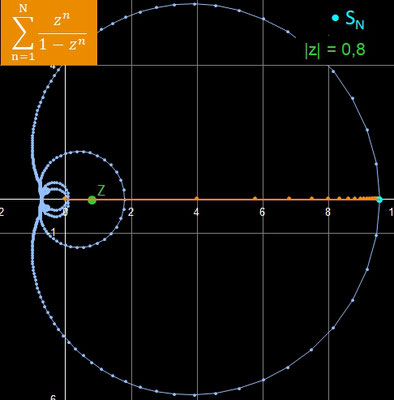
In der folgenden Galerie sind die Ergebnisse für r_z = 0.8 mit Δ φ = 2° und r_z = 0.95 mit Δ φ = 1° und jeweils N = 500 dargestellt.

Die Konvergenzbedingung ist gleichbedeutend mit

- 0.5 < ℜe (z).

Animation:

N = 50

r_Z = 0.5

Δ φ = 2π / 360 = 1°

Animation:

r_z = 0.6 N = 20 Δ φ = 2 π / 180 = 2°

Animation:

r_Z = 0.9 N = 200 Δ φ = 2 π / 180 = 2°

Animation:

r_z = 1 N = 20 Δ φ = 2 π / 180 = 2°

Animation:

r_z = 1 N = 200 Δ φ = 2 π / 180 = 2°

[4]

Animation:

r_z = 1

N = 100

Δ φ = 2 π / 180 = 2°

Die Summe konvergiert für N → ∞, falls |z| < 1.

Animation:

r_z = 0.95

N = 8 (für größere Werte von N liegen die

berechneten Partialsummen oberhalb

des darstellbaren Zahlenbereichs!)

Δ φ = 2 π / 180 = 2°

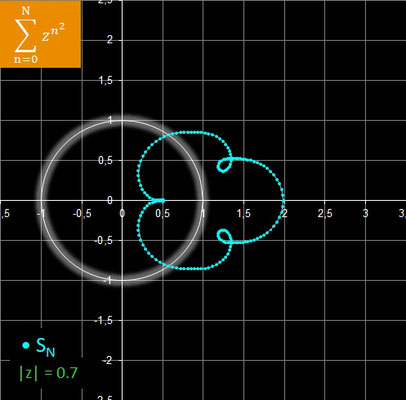
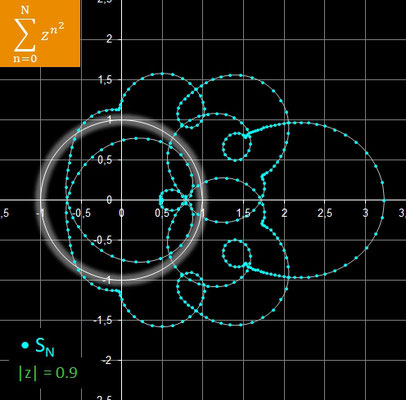
In der folgenden Galerie sind die Ergebnisse für r_z = 0.7, r_z = 0.8 und r_z = 0.9 mit jeweils N = 8 dargestellt.

Diese Reihe ist die Potenzreihe [5] für die Exponentialfunktion e^z mit dem Konvergenzradius
r = ∞, d.h. die Reihe konvergiert für alle z ∈ ℂ:

Animation:

r_z = 2

N = 20

Δ φ = 2 π / 180 = 2°

[6], [7]

Animation:

N = 100

r_z = 0.97

Δ φ = 2π / 720 = 0.5°

Animation:

N = 200

r_z = 0.98

Δ φ = 2π / 360 = 1°

Animation:

N = 500

r_z = 1.5

Δ φ = 4°

Animation:

N = 500

r_z = 0.7

Δ φ = 2°

Die folgende Animation zeigt die berechneten Grenzwerte der Reihe (lim) für r_z = 0.25 bis 2.9, wobei für
z = 1 und z = 2 die Reihe jeweils divergiert.

Quellenverweise

[1] Einführung in die Funktionentheorie / Folgen und Reihen mit komplexen Gliedern

[2] https://de.wikipedia.org/wiki/Lambert-Reihe

[3] https://de.wikipedia.org/wiki/Digamma-Funktion

[4] https://en.wikipedia.org/wiki/Polylogarithm

[5] https://de.wikipedia.org/wiki/Potenzreihe

[6] https://en.wikipedia.org/wiki/Theta_function

[7] https://www.wolframalpha.com/input?i=EllipticTheta+function