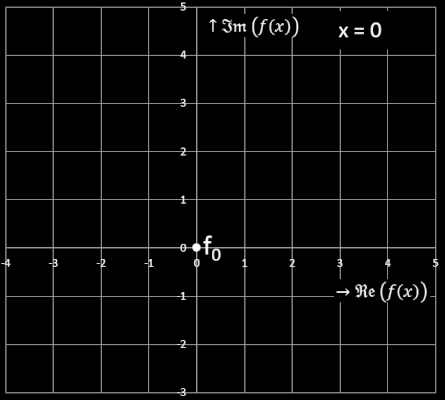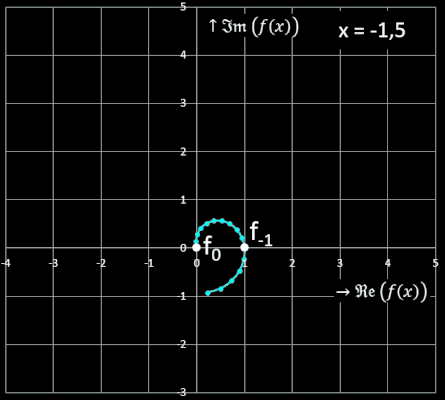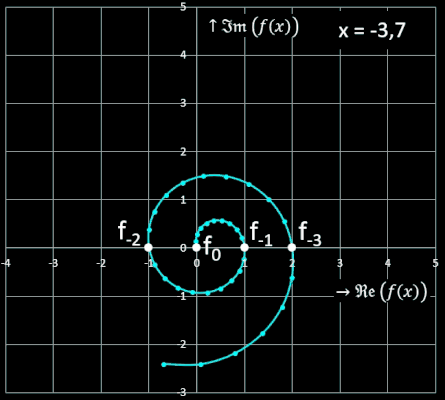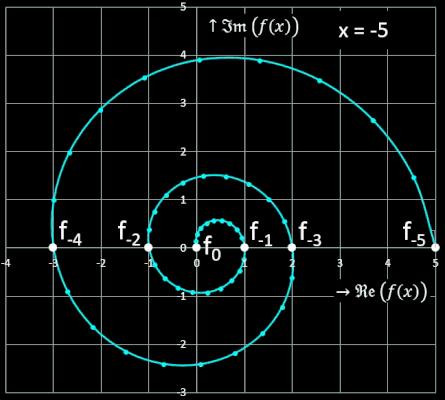Komplexe Fibonacci-Folgen
Vor der Betrachtung komplexer Fibonacci-Folgen wird zunächst auf die natürlichen / ganzzahligen Fibonacci-Folgen und deren Erweiterung zu kontinuierlichen Fibonacci-Folgen eingegangen.
Natürliche und ganzzahlige Fibonacci-Folgen
Die Fibonacci Folge ist eine Folge natürlicher Zahlen mit folgender rekursiver Bildungsvorschrift:
Die ersten 17 Glieder der Folge ergeben sich somit zu:
Oftmals wird die Fibonacci-Folge (z.B. in der Schule) an Hand einer Kaninchenpopulation dargestellt:
Es startet ein männliches und ein weibliches Kaninchenneugeborenes (ein Paar).
Angenommen
- ein Neugeborenes braucht einen Monat um auszuwachsen,
- ein Paar bekommt pro Monat ein Paar Neugeborenes
- und kein Kaninchen stirbt.
Im 1. Monat gibt es also ein Paar Neugebore, im 2. Monat sind sie Erwachsene, es gibt also keine Neugeborenen. Dann bekommen sie ein Paar Neugeborene im 3. Monat und so weiter (vgl. mit nachfolgender Grafik). In dem hier vereinfachten Beispiel beschreibt die Fibonacci-Folge die Gesamtpopulation der Kaninchenpaare.
Stellt man die rekursive Bildungsvorschrift der Fibonacci-Folge um fn-2 = fn – fn-1 , so lassen sich die
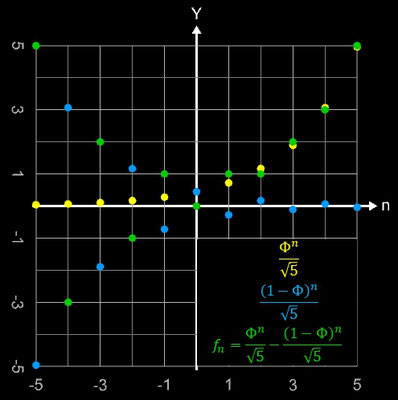
Fibonacci-Zahlen in den Bereich der negativen ganzen Zahlen 𝕫– erweitern, so dass sie für alle n ∈ 𝕫 definiert sind. Man erhält:
Die Beträge der Werte sind symmetrisch, im Negativen alternieren sie jedoch; somit gilt f–n = (–1)n+1 fn .
Eigenschaften, Anwendungen und Verbindungen/Bezüge zu anderen Bereichen der Mathematik finden interessierte Leser in [1] sowie in "The Online Encyclopedia of Integer Sequences" [2].
Eine wichtige Eigenschaft der Fibonacci-Folge ist, dass die Folge der Verhältnisse zweier aufeinanderfolgender Fibonacci-Zahlen fn und fn+1
in ℝ mit folgendem Grenzwert konvergiert:
Die irrationale Zahl Φ ≈ 1.61803... wird auch Goldener Schnitt [3] genannt. Im Negativen nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen gegen Φ-1.
Eine weitere Beziehung der Fibonacci-Folge mit dem Goldenen Schnitt zeigt die Formel von Moivre-Binet, mit der sich das n-te Glied der Folge unmittelbar bestimmen lässt ohne die n-1 vorhergehenden Glieder berechnen zu müssen. Es gilt:
Für einen Beweis mittels Vollständiger Induktion klicken Sie bitte auf das Minibild in der rechten Spalte.
Zerlegt man den Bruch in der Moivre-Binet-Formel in zwei Teilbrüche, so entsteht die Differenz zweier Folgen. Bemerkenswert ist hier, dass für n ∈ ℤ die Differenz der Glieder beider Folgen mit jeweils der n-ten Potenz einer irrationalen Zahl Φ ganzzahlige Fibonacci-Zahlen erzeugen (vgl. mit der folgenden Grafik).
Für positive n geht der Einfluss der Folge (1 - Φ)n / √5 rasch gegen Null. Dies kann man verwenden, um die Berechnung abzukürzen, indem man den Term für genügend große n ignoriert und das Ergebnis zur nächsten natürlichen Zahl rundet:
Dies gilt bereits für 0
≤ n
∈
ℤ .
In der folgenden Tabelle sind für die ersten Folgeglieder die nicht gerundeten Werte fn*
aufgeführt.
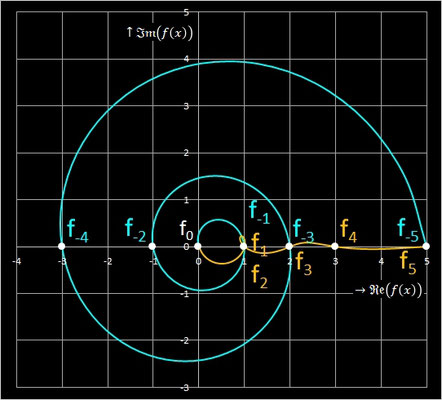
Kontinuierliche Fibonacci-Folgen
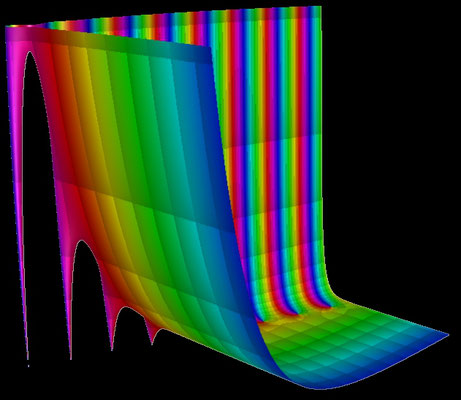
Setzt man in den Exponenten n der Moivre-Binet-Formel nicht-ganzzahlige Werte ein, so wandelt sich die Fibonacci-Folge in eine kontinuierliche Funktion um. Da 1−Φ jedoch negativ ist und nicht-ganzzahlige Potenzen negativer Zahlen nur im Komplexen definiert sind, muss der Wertebereich auf ℂ erweitert werden:
Der Graph dieser Funktion stellt sich mit x als Kurvenparameter wie folgt dar:
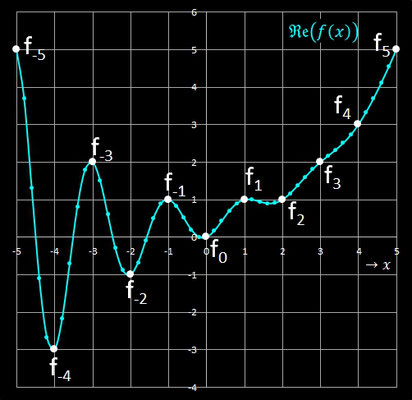
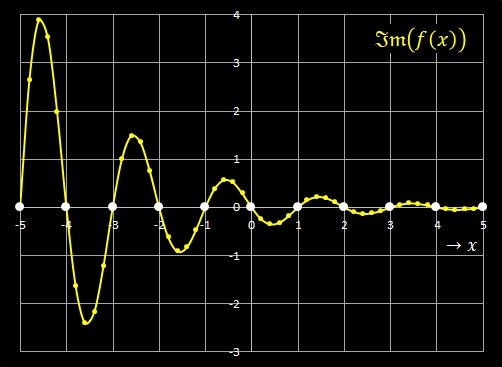
Für reelle x kann man f umformen:
und erhält so folgende Darstellung:
Komplexe Fibonacci-Folgen
Die zuvor beschriebene Erweiterung der Fibonacci-Folge zu einer komplexwertigen Funktion mit reellen Eingabewerten kann nochmals erweitert werden, indem man als Definitionsbereich von f die komplexen Zahlen ℂ zulässt:
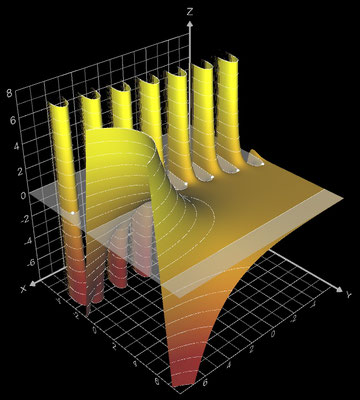
Um diese Funktion darstellen zu können, werden die komplexen Funktionswerte f (z) auf reelle Werte heruntergebrochen, d.h. die komplexwertige Funktion f : ℂ → ℂ wird durch die Funktion f̃ : ℝ² → ℝ ersetzt (s. auch 3D Visualisierung komplexwertiger Funktionen).
Die darzustellenden Größen für f (z) mit z = x + y ∙ i ergeben sich zu:
Mit
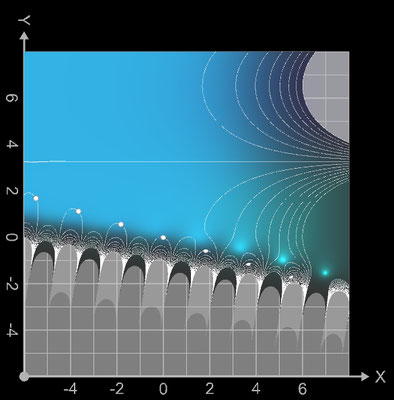
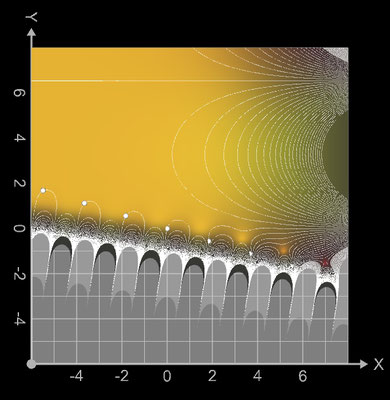
liegen die Nullstellen zn auf einer Geraden durch den Nullpunkt; dies kann man gut in den
Contour-Plots erkennen:
Der Absolutbetrag der komplexen Fibonacci-Folge
ist in der folgenden Galerie links dargestellt. Das rechte Bild der Galerie zeigt den Absolutbetrag zusammen mit der Phase (s. auch 3D Visualisierung komplexwertiger Funktionen).
Eine Darstellung von f als Phasen-Plot (s. auch 2D Visualisierung komplexwertiger Funktionen) zeigt die folgende Abbildung.
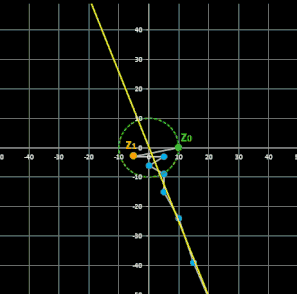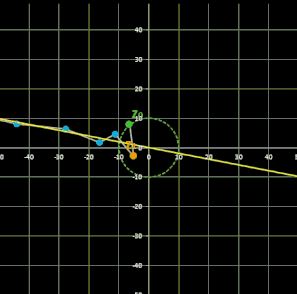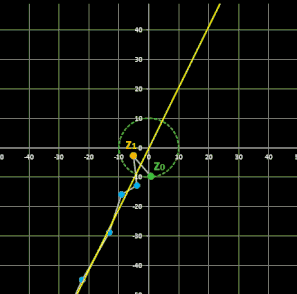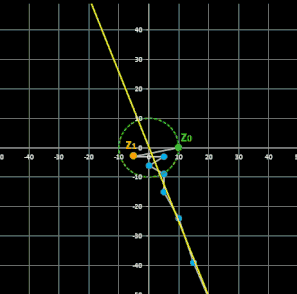
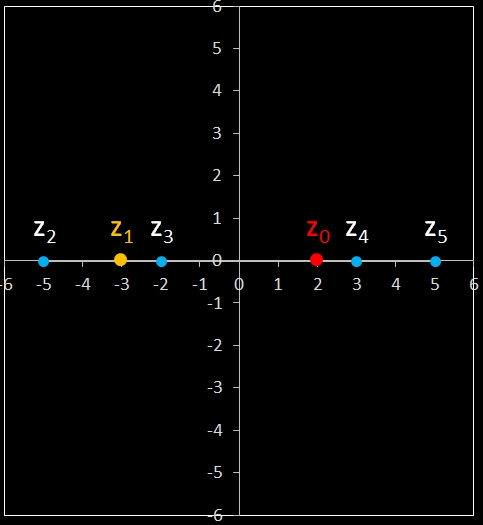
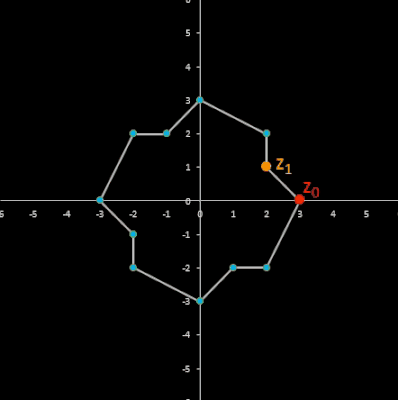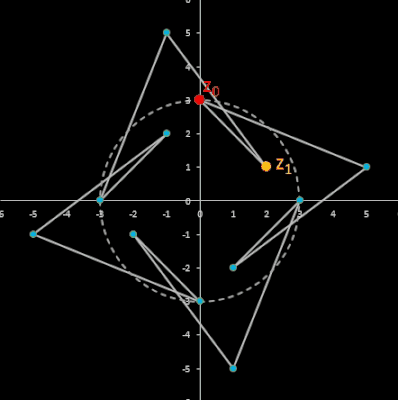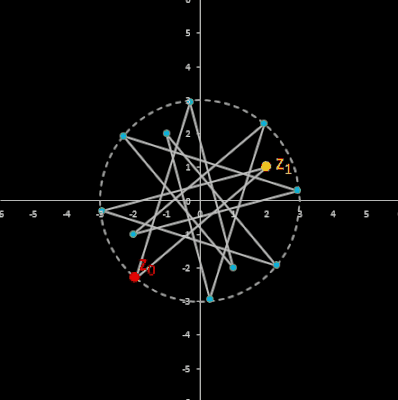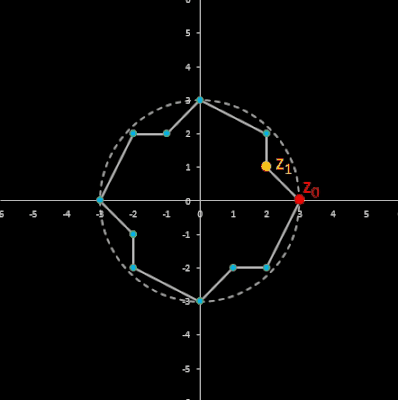
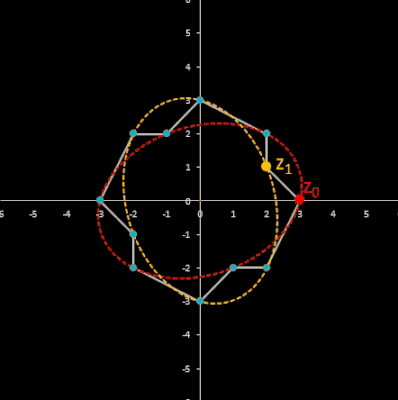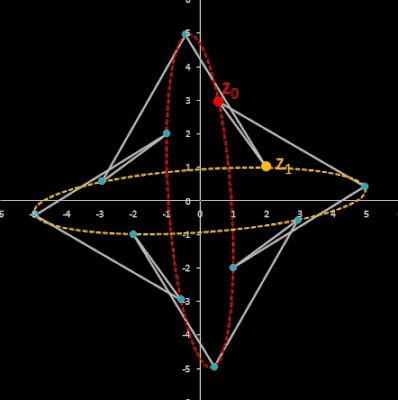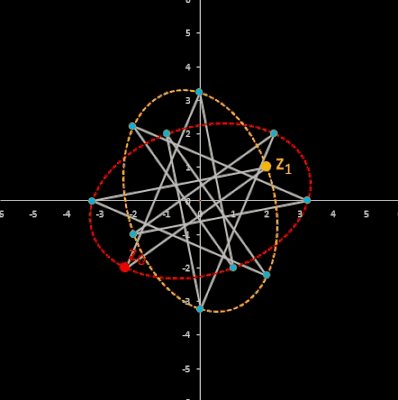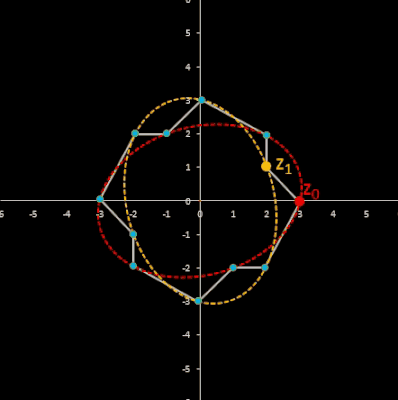
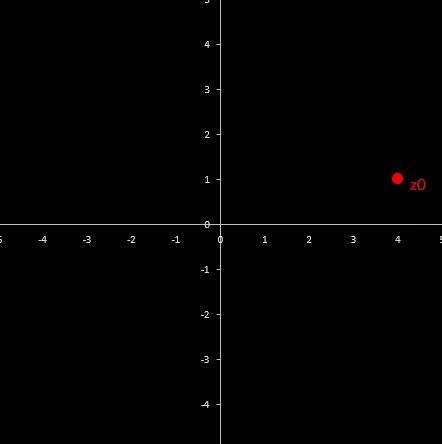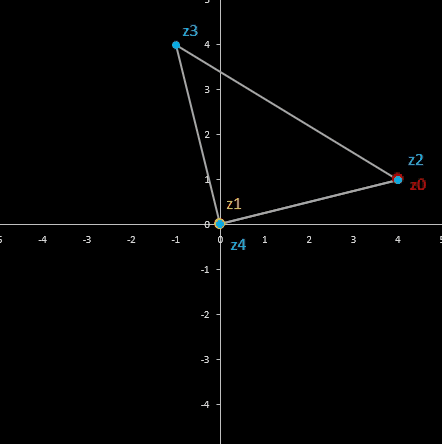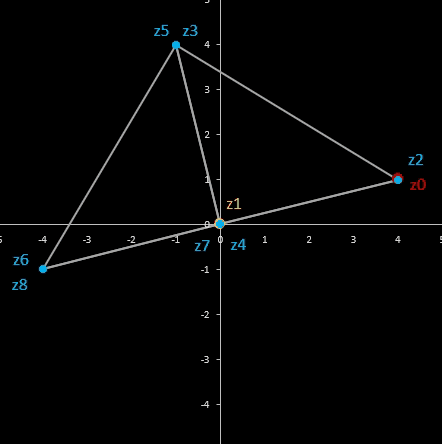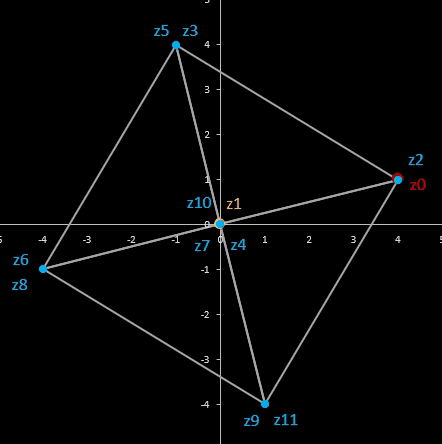
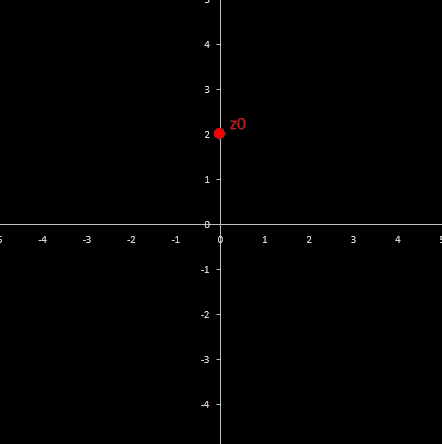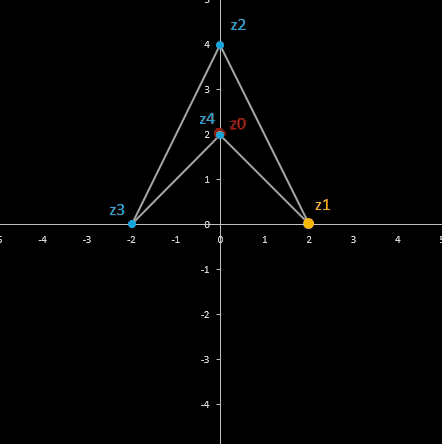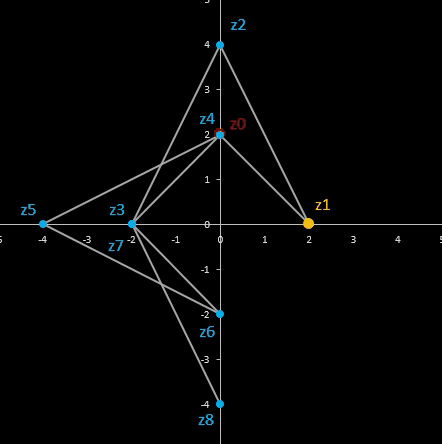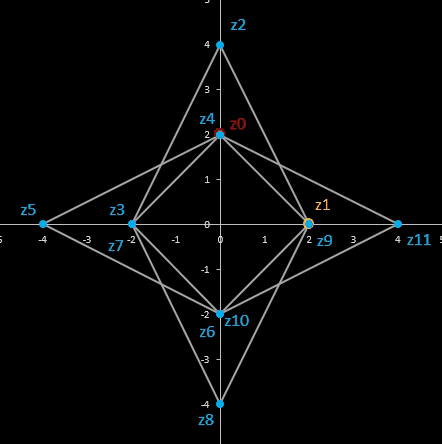
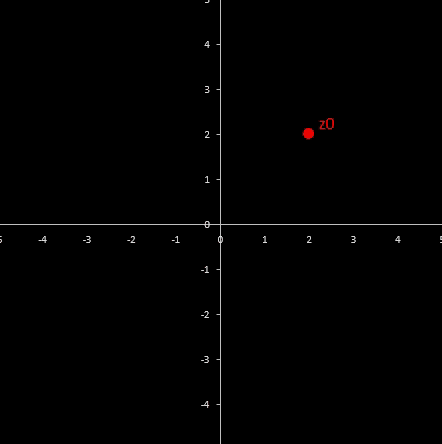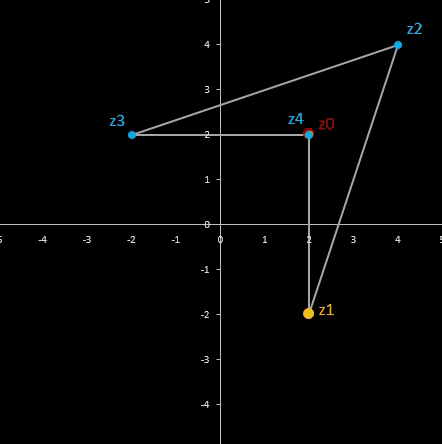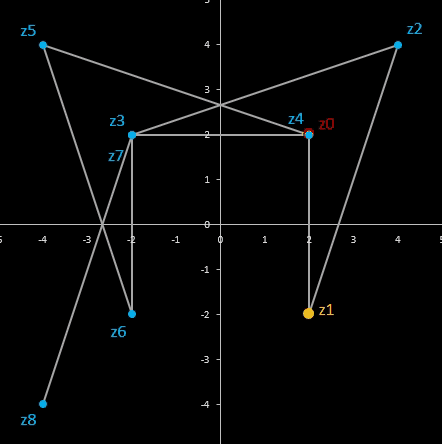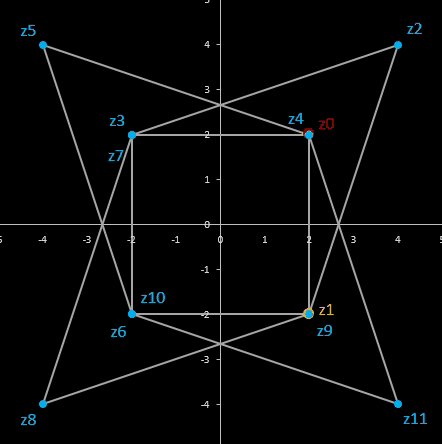
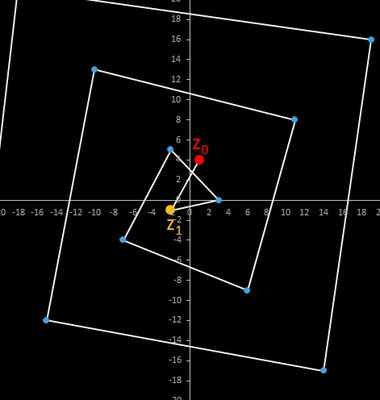
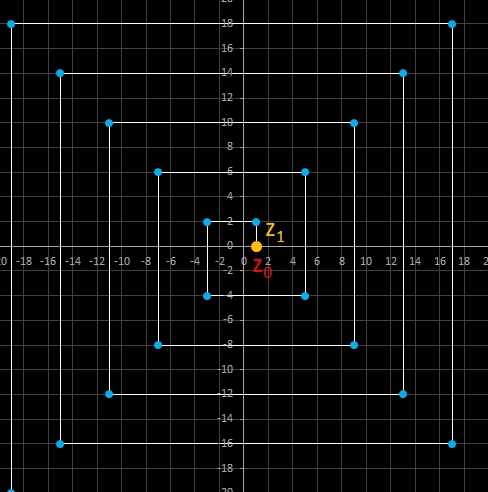
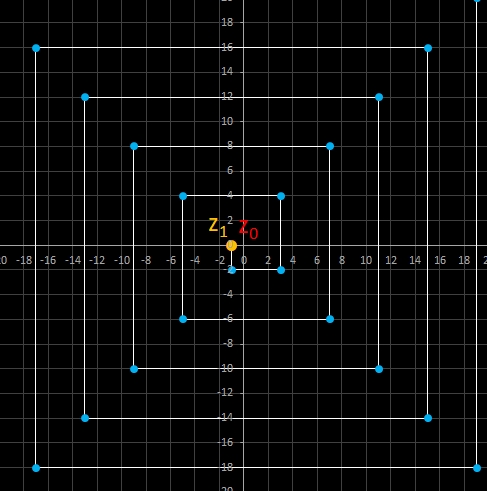
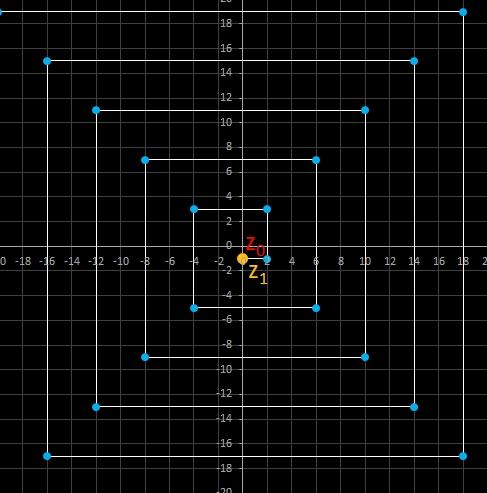
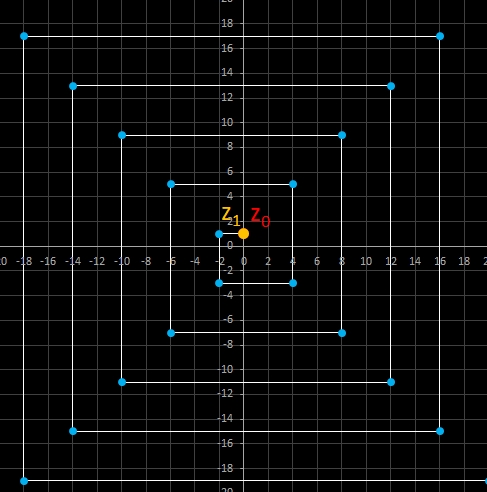
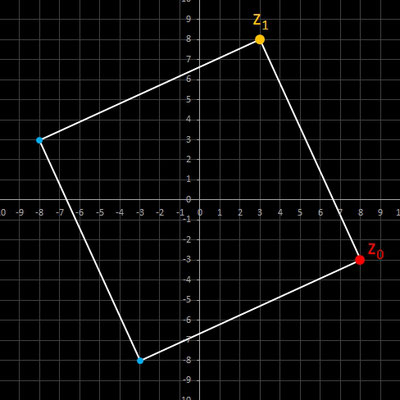
Für komplexe Startwerte zn+2 = zn+1 + zn entsteht in der Gaußschen Ebene eine Punktfolge, welche sich einer Geraden annähert. Um die Steigung dieser Geraden zu ermitteln, betrachte man die Folge
z0 = z0
z1 = z1
z2 = z0 + z1
z3 = z0 + 2 z1
z4 = 2 z0 + 3 z1
z5 = 3 z0 + 5 z1
…
zn = fn-1 z0 + fn z1
wobei fn die gewöhnliche Fibonacci-Folge ist.
Für n ≫ 0 ist fn ≈ Φ fn-1.
Mit den Startwerten z0 = a + b i und z1 = c + d i gilt somit:
zn = fn-1 z0 + fn z1 ≈ fn-1 (z0 + Φ z1) = fn-1 ( (a + Φ c) + i (b + Φ d) ).
Da fn-1 lediglich ein reeller Faktor ist, gilt für das Argument von zn und somit für die Steigung:
Im animierten Beispiel oben rechts läuft z0 auf einem Kreis mit dem Radius 10 entlang während z1 = -5 - 3 i konstant bleibt. Die Folgenglieder z1 sind in blau, die Gerade ist in gelb eingezeichnet.
Erweiterte Fibonacci-Folgen
Außer der Wahl beliebiger Startwerte besteht eine weitere Art der Erweiterung der Fibonacci-Folge darin, die Glieder zn+1 und zn mit Faktoren zu versehen:
zn+2 = a zn+1 + b zn mit a, b ∈ ℂ
In Abhängigkeit der Koeffizienten a und b kann eine solche Folge divergieren, konvergieren oder zyklisches Verhalten zeigen. Dazu im Folgenden ein paar Beispiele.
Punktkonvergenz, Nullfolge
a = 0,9 + 0,9 i b = - 0,9 i
z0 = 1,5 + 1,5 i z1 = -1 + i | z500 | ≈ 7,9 • 10-12
Punktkonvergenz, Nullfolge
a = 1 - 0,6 i b = 0,4 i
z0 = 0,5 - i
z1 = 1 + 1,5
i | z500 |
≈ 10-15
In seiner Publikation "Allgemeine Fibonacci-Folgen" [7] untersucht der Verfasser H. Walser dieses Grenzverhalten systematisch und stellt entsprechende Bedingungen auf. Darüber hinaus finden Interessierte Leser(innen) auf seiner Webseite unter "Miniaturen" eine unglaublich große Vielfalt an Themen rund um die Fibonacci-Folge.
Im weiteren Verlauf dieser Webseite liegt der Focus auf speziellen Folgen, die ein zyklisches Verhalten aufweisen.
Zyklische Fibonacci-Folgen
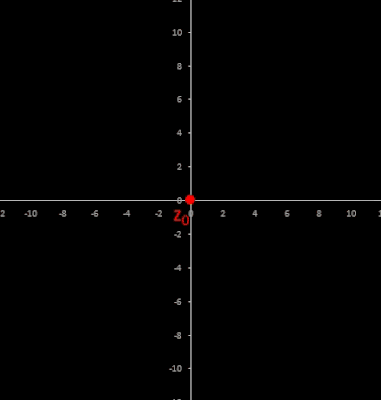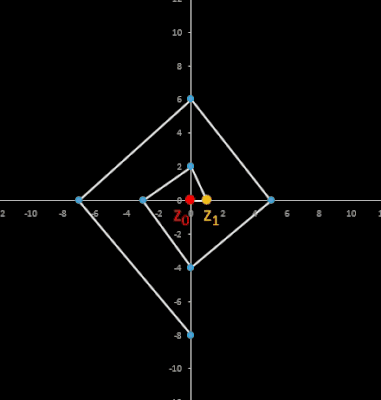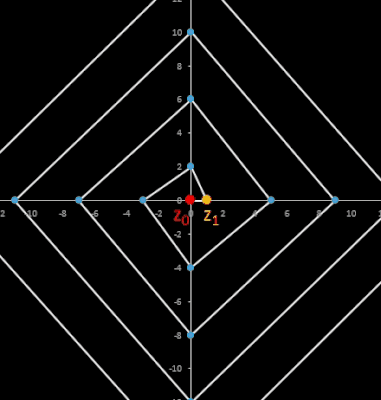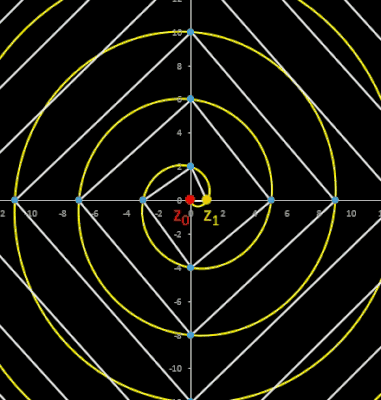
Durch eine entsprechende Wahl von a und b für die Folge zn+2 = a zn+1 + b zn entstehen zyklische Fibonacci-Folgen. Verbindet man je zwei aufeinander folgende Glieder zn und zn+1 einer zyklischen Fibonacci-Folge mit der Zykluslänge λ = m durch eine Strecke, so ergibt dies ein Polygon [4] mit m Ecken und Seiten (m-Eck).
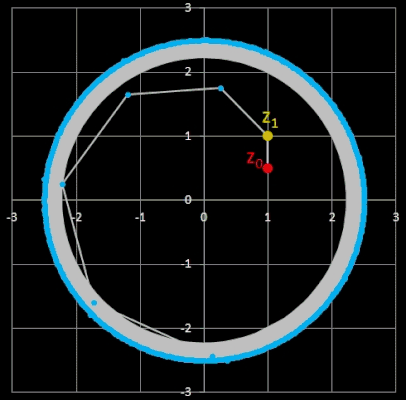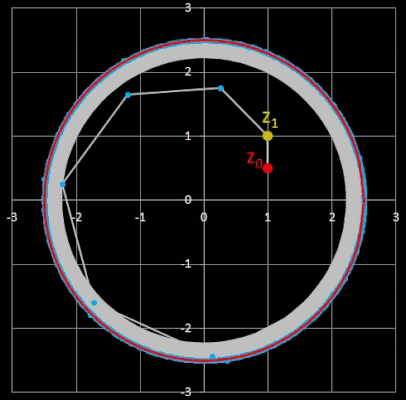
• Folge zn+2 = zn+1 - zn mit n ∈ ℕ0, zn ∈ ℂ
Durch Multiplikation von zn mit -1 entsteht eine zyklische Folge, die unabhängig von den Startwerten z0 und z1 stets die Zykluslänge λ = 6 besitzt:
z0 = c mit c ∈ ℂ
z1 = d mit d ∈ ℂ
z2 = d – c
z3 = d – c – d = -c
z4 = -c – (d – c) = -d
z5 = -d – (-c) = -d + c
z6 = -d + c – (-d) = c
z7 = c – (-d + c) = d
In der Galerie werden nacheinander gezeigt:
-
Beispiel
der Folge mit rein reellen Startwerten
(z0 = 2, z1 = -3). -
Beipiel der
Folge mit komplexen Startwerten
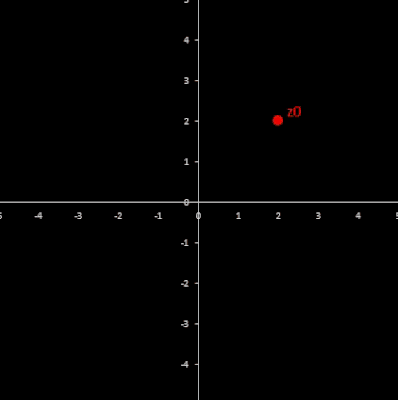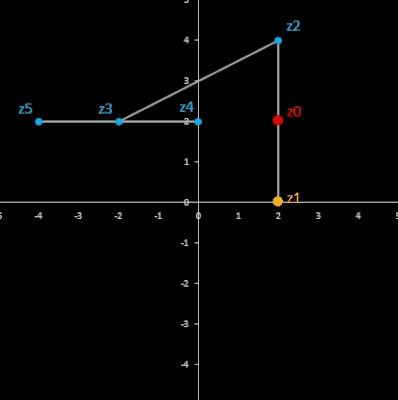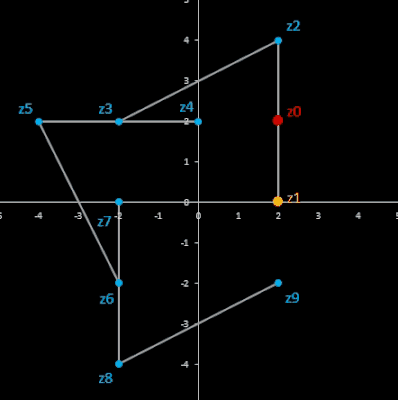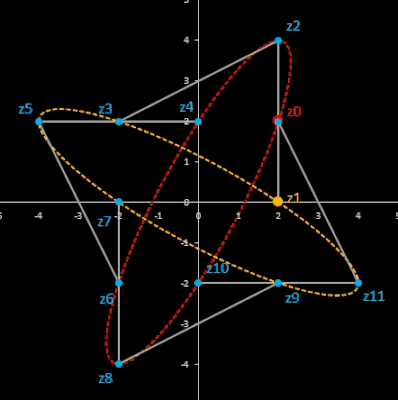
(z0 = 2 + 5 i, z1 = -3 + 2 i); die Verbindungslinien zwischen je zwei Gliedern bilden ein Sechseck. -
dto. mit Ellipse
Alle sechs Punkte liegen auf einer Ellipse mit der parametrischen Darstellung
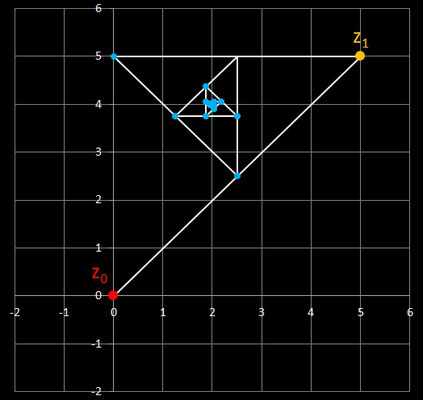
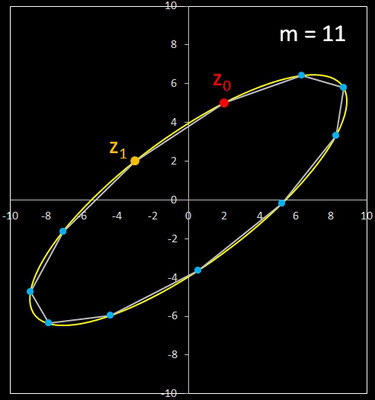
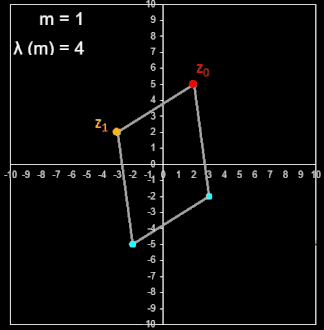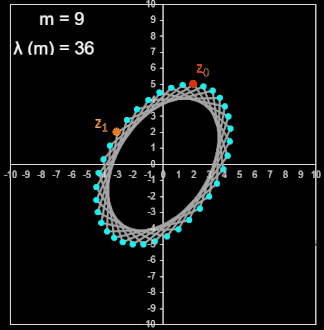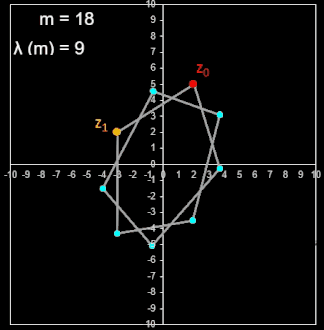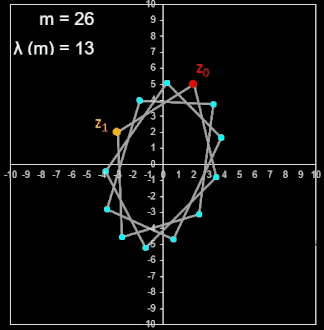
• Folge zn+2 = 2 cos (φ) zn+1 - zn mit n ∈ ℕ0, m ∈ ℕ, zn ∈ ℂ, φ = 2π / m
Die Zykluslänge λ dieser Folge beträgt stets λ (m) = m. Für m = 6 ergibt sich, da cos ( π / 3) = 0.5, die zuvor betrachtete Folge. Hier drei weitere Beispiele mit ebenfalls z0 = 2 + 5 i, z1 = -3 + 2 i :
Während die Rekursion zn+2 = 2 cos (φ)
zn+1 - zn mit
beliebigen Startwerten in der Gauß'schen Zahlenebene die Eckpunkte affin-regulärer m-Ecke erzeugt, liefert sie mit den Startwerten z0 = 1 und
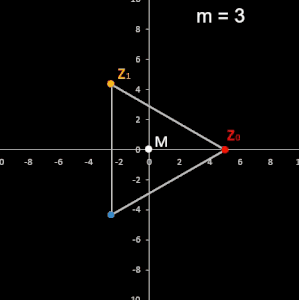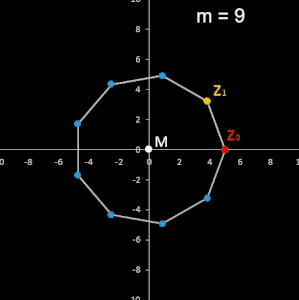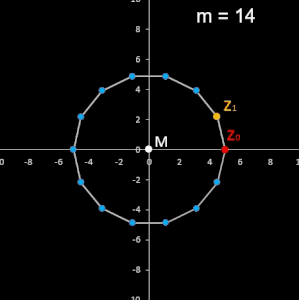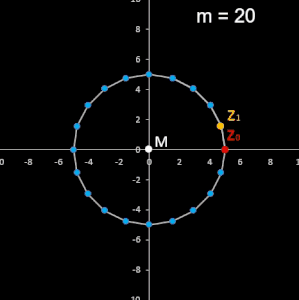
z1 =
e i φ die m-ten Einheitswurzeln. Die Folge ist zyklisch mit der Zykluslänge m und liefert in der
Gauß'schen Zahlenebene ein reguläres Polygon, d.h. alle Seiten und Innenwinkel gleich
groß, mit m Ecken (m-Eck) und dem Zentrum M im Ursprung:
• Folge zn+2 = 2 sin (φ) zn+1 - zn mit n ∈ ℕ0, m ∈ ℕ, m ≠ 2, zn ∈ ℂ, φ = π / m
Bei dieser Folge wurde die Cosinus-Funktion durch die Sinus-Funktion ersetzt; zusätzlich wurde dessen Argument halbiert: φ = π / m. Die Zykluslänge der Folge ist nun etwas komplizierter:
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| λ | 4 | n.d. | 12 | 8 | 20 | 6 | 28 | 16 | 36 | 5 | 44 | 24 | 52 | 14 | 60 | 32 | 68 | 9 | 76 | 40 | 84 | 22 | 92 |
48 |
100 |
13 |
Für λ (m) folgt somit:
Die Folge liefert mit beliebigen Startwerten in der Gauß'schen Zahlenebene die Eckpunkte affin-regulärer m-Ecke mit Mittelpunkt im Ursprung:
• Folge zn+2 = (1 + e i φ) zn+1 - e i φ zn mit m ∈ ℕ, m > 2, zn ∈ ℂ, φ = 2π / m
Formt man diese Rekursionsvorschrift der verallgemeinerten komplexen Folge um:
zn+2 = zn+1 + ei φ zn+1 – ei φ zn
zn+2 – zn+1 = (zn+1 – zn) ei φ
so zeigt sich, dass die Strecke von zn+2 zu zn+1 (also die Seite des m-Ecks) die um den Winkel φ = 2π /m gedrehte vorherige Strecke von zn+1 zu zn ist. Für m ergibt sich ein gleichseitiger Streckenzug mit jeweiliger Richtungsänderung φ, der sich zu einem regulären m-Eck schließt:
Der Mittelpunkt M des m-Ecks liegt bei
.
• Folge zn+2 = (1 + e i k φ) zn+1 - e i k φ zn
mit m, k ∈ ℕ, m > 2, 1 ≤ k < m, zn ∈ ℂ, φ = 2π / m
Für beliebige Startwerte z0 und z1 lassen sich mit dieser verallgemeinerten Fibonacci-Rekursion m - 1 reguläre planare Polygone erzeugen. Dabei lassen sich zwei Typen unterscheiden:
-
einfache reguläre Polygone, deren Kanten sich nur in den Eckpunkten (Folgengliedern) berühren
- überschlagene reguläre Polygone, d.h. jeder Eckpunkt wird mit einem nicht benachbarten Eckpunkt verbunden, so dass es zu jeder Kante zusätzliche Schnittpunkte durch Überschneidungen gibt; wegen ihres Aussehens nennt man diese Polygone auch Sternpolygone [5].
Sind m und k teilerfremd, so liegt bei dieser Folge stets ein Sternpolygon vor.
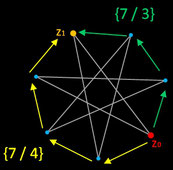
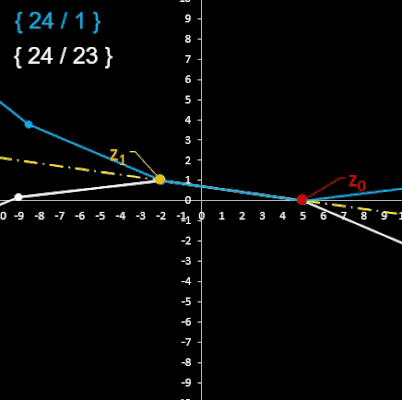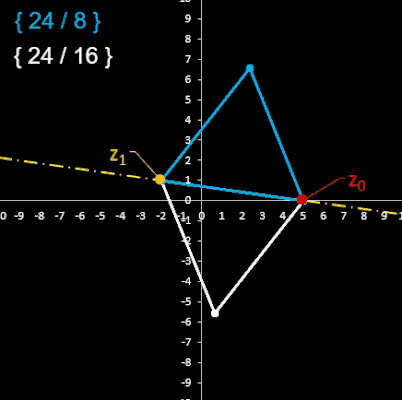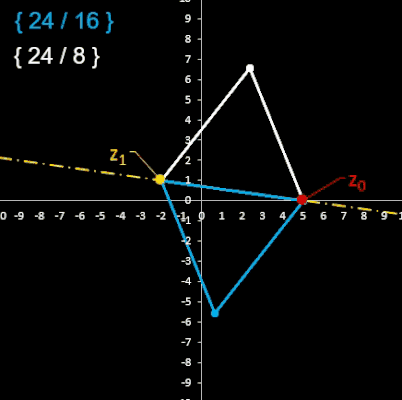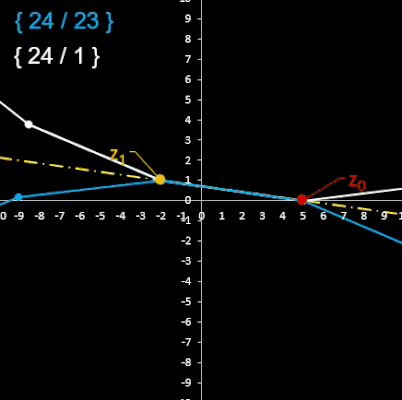
Die Kennzeichnung / Klassifizierung eines Sternpolygons ermöglicht das Schläfli-Symbol [6] :
{ p / q } mit p gleich der Anzahl der Ecken,
jede q-te Ecke wird mit einer Geraden verbunden.
Hierbei gibt es zwei Zählrichtugen bezüglich der Größe q (s. Beispiel in Grafik rechts), d.h. zu { p / q } existiert auch { p / q' } mit q + q' = p.
Ist der der Wert des Bruchs p / q eine natürliche Zahl, so liegt ein einfaches p-Eck vor, ansonsten ein Sternpolygon.
Für ein festes m lassen sich für k = 1, ..., m-1 folgende Polygone erzeugen:
-
m gerade: m / 2 Paare gleicher Polygone
-
m ungerade: m / 2 - 1 Paare gleicher Polygone und ein Zweieck.
Die folgende linke Animation zeigt für m = 9 und k = 1, ..., 8 die entstehenden Polygone. In der rechten Animation mit m = 24 bricht diese bei m / 2 = 12 ab und erzeugt so nur jeweils eine Hälfte der möglichen Paare (vgl. mit Tabelle weiter unten).
Die folgende Animation zeigt für m = 24 und k = 1, ..., 23 die entstehenden Polygone. Hierbei werden die Polygon-Paare mit Schläfli-Index {m / k} und {m / m-k} gleichzeitig dargestellt, wobei die Gerade durch z0 und z1 die Symmetrieachse ist.
Die folgenden beiden Tabellen zeigen noch einmal paarweise die generierten Polygone der Animationen. Die Anzahl der Ecken p sowie die Größe q lässt sich aus den Folgeparametern m und k herleiten:
|
m
= 9 |
||||
| k | 1 | 2 |
3 |
4 |
| p | 9 | 9 | 3 | 9 |
| q | 1 | 2 | 1 | 4 |
|
|
|
|
|
|
| k | 8 | 7 | 6 | 5 |
| p | 9 | 9 | 3 | 9 |
| q | 8 | 7 | 2 | 5 |
|
|
|
|
|
|
| m = 24 | |||||||
| k | p | q | k | p' | q' | ||
| 1 | 24 | 1 |
|
23 | 24 | 23 |
|
| 2 | 12 | 1 |
|
22 | 12 | 11 |
|
| 3 | 8 | 1 |
|
21 | 8 | 7 |
|
| 4 | 6 | 1 |
|
20 | 6 | 5 |
|
| 5 | 24 | 5 |
|
19 | 24 | 19 |
|
| 6 | 4 | 1 |
|
18 | 4 | 3 |
|
| 7 | 24 | 7 |
|
17 | 24 | 17 |
|
| 8 | 3 | 1 |
|
16 | 3 | 2 |
|
| 9 | 8 | 3 |
|
15 | 8 | 5 |
|
| 10 | 12 | 5 |
|
14 | 12 | 7 |
|
| 11 | 24 | 11 |
|
13 | 24 | 13 |
|
| 12 | 2 | 1 |
|
|
|||
Bezüglich der Art (einfaches oder Sternpolygon) der für ein gegebenes m und k = 1, ..., m-1 mit dieser Folge generierten Polynome gelten die folgenden Aussagen:
- Polygone mit Schläfli-Index {m / 1} und {m / m-1} sind einfache Polygone.
- Das Polygon ist ein Sternpolygon ⇒ m ≥ 5
- ggT (m, k) = 1 (d.h. m und k sind teilerfremd) ⇒ es liegt ein Sternpolygon vor
- q = 1 v p – q = 1 ⇔ es liegt ein einfaches Polygon vor
Die Frage, wie viele Sternpolynome die Folge für ein gegebenes m und k = 1, ..., m-1 generiert, ist hingegen nicht ohne weiteres zu beantworten. Grundsätzlich gilt:
Ist m eine Primzahl, dann lassen sich für dieses m mit der Folge m-3 Sternpolygone generieren.
Dies ist unmittelbar einsehbar, da von den möglichen m-1 Polygonen die Polygone mit {m / 1} und {m / m-1} einfache Polygone sind.
In der folgenden Tabelle sind von m abhängige Größen aufgeführt (orangene Schrift: m ist Primzahl):
- s: Anzahl der Sternpolygone
- a: Anzahl der Primzahlen, die kleiner/gleich m sind
- t: Anzahl der Teiler von m
- f: Anzahl der Primfaktoren für m
- PZ: Primfaktorzerlegung für m
- T: Menge der Teiler von m
| m | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | .. | 30 | .. | 42 | .. | 100 |
| s | 2 | - |
4 |
2 | 4 | 4 | 8 | 2 | 10 | 8 | 8 | 8 | 14 | 8 | 16 | 10 | 14 | 16 | 20 | 10 | .. | 16 | .. | 28 | .. | 86 |
| a | 3 | 4 | 4 | 4 | 5 | 6 | 6 | 6 | 7 | 8 | 8 | 8 | 9 | .. | 10 | .. | 13 | .. | 25 | |||||||
| t | 2 | 2 | 2 | 2 | 4 | 2 | 2 | 3 | 4 | 4 | 2 | 2 | 6 | .. |
6 |
.. | 6 | .. | 6 | |||||||
| f | 2 | 3 | 2 | 2 | 3 | 2 | 2 | 4 | 3 | 3 | 2 | 2 | 4 | .. | 3 | .. | 3 | .. | 4 | |||||||
| PZ |
2 3 |
2 2 2 |
3 3 |
2 5 |
2 2 3 |
2 7 |
3 5 |
2 2 2 2 |
2 3 3 |
2 2 5 |
3 7 |
2 11 |
2 2 2 3 |
.. |
2 3 5 |
.. |
2 3 7 |
.. |
2 2 5 5 |
|||||||
| T |
1 2 3 6 |
1 2 4 8 |
1 3 9 |
1 2 5 10 |
1 2 3 4 6 12 |
1 2 7 14 |
1 3 5 15 |
1 2 4 8 16 |
1 2 3 6 9 18 |
1 2 4 5 10 20 |
1 3 7 21 |
1 2 11 22 |
1 2 3 4 6 8 12 24 |
.. |
1 2 3 5 6 10 15 30 |
.. |
1 2 3 6 7 14 21 42 |
.. |
1 2 4 5 10 20 50 100 |
Für die Anzahl s der für ein m mit k = 1, ..., m-1 generierbaren Sternpolygone stellt r-3 eine obere Schranke dar, wobei r die zu m nächsthöhere Primzahl ist.
Bisher ist es mir noch nicht gelungen, einen funktionalen Zusammenhang s (m) herzustellen bzw. Argumente dafür zu finden, dass ein solcher funktionaler Zusammenhang überhaupt existiert. Falls sich interessierte Leser(innen) daran versuchen möchten, schicke ich auch gerne zur Unterstützung entsprechende EXCEL-Tabellen mit VBA-Programmen zu...
• Folge zn+2 = i zn+1 + zn mit n ∈ ℕ0, zn ∈ ℂ
Gemäß der rekursiven Bildungsvorschrift ergibt sich für diese Folge:
z0 = a + b i
z1 = c + d i
z2 = a + b i + c i - d
z3 = a i - b
z4 = c i - d
z5 = a i - b - c - d i
z6 = - a - b i
z7 = - c - d i
z8 = d - b i - c i - a
z9 = b - a i
z10 = d - c i
z11 = b - a i + c + d i
z12 = a + b i = z 0
z13 = c + d i = z 1
Dies bedeutet, dass die Zykluslänge der Folge für beliebige Startwerte z0 und z1 stets λ = 12 ist.
In der Gauß'schen Zahlenebene liegen die Punkte der Glieder abwechslungsweise auf zwei kongruenten aber um π/2 verdrehten Ellipsen. Mit φ = 2 π / 12 und zwei aufeinander folgenden Gliedern mit geraden Indices k (bzw. ungeraden Indices k für die andere Ellipse) zk = a + b i und zk+2 = c + d i lautet mit t = 0 … 2 π die Ellipsengleichung:
Bei den folgenden Animationen ist z1 konstant (2 + i) während sich z0 auf einem Kreis mit Radius 3 um den Ursprung des Koordinatensystems bewegt.
DIe folgende Galerie enthält weitere Beispiele zyklischer Folgen mit speziellen Symmetrien.
• Folge zn+2 = 2 i zn+1 + zn mit n ∈ ℕ0, zn ∈ ℂ
Verdoppelt man bei der vorigen Folge den imaginären Faktor vor zn+1, so ist
die Folge mit z0 = (0, 0) und
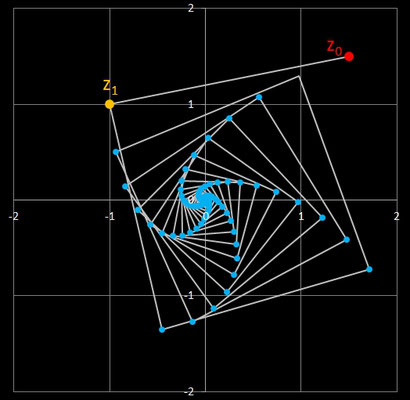
z1 = (1, 0) nicht mehr zyklisch, liefert folglich kein Polygon, sondern eine eckige Spirale:
Auch wenn man bei "schnellem Hinsehen" meint, dass es sich um eine rechteckige, Archimedische Spirale handelt (d.h. je zwei benachbarte "Windungen" sind parallel), so ist dies nicht der Fall: keine der benachbarten Seiten sind parallel. Vielmehr liegen hier die Folgenglieder auf einer Archimedischen Spirale (gelb in Grafik) der Form
Bei entsprechender Wahl der Startwerte erkennt man bei Betrachtug der entstehenden Spirale deutlich besser, dass es sich nicht um eine rechteckige Archimedische Spirale handelt, wie z.B. in der folgenden Grafik mit z0 = (1, 4) und z1 = (-2, -1)):
Dennoch liefert die Rekursion, abhängig von den Startwerten z0 und z1, auch rechteckige, Archimedische Spiralen für die folgende Fälle:
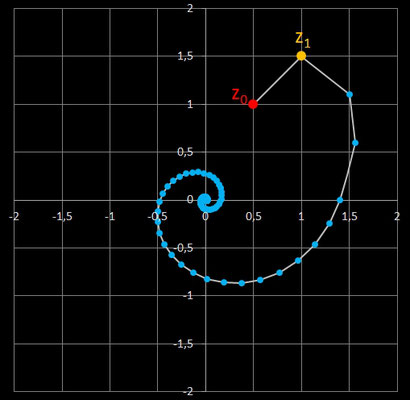
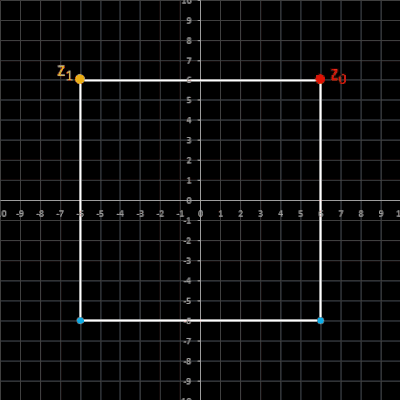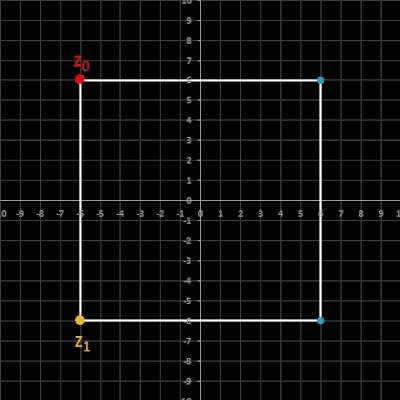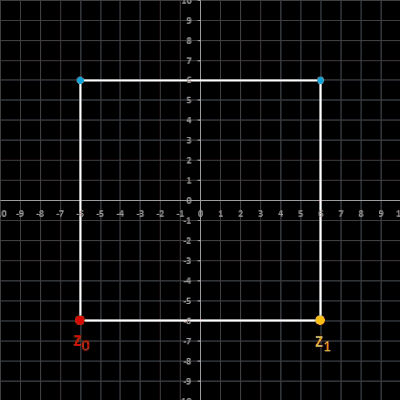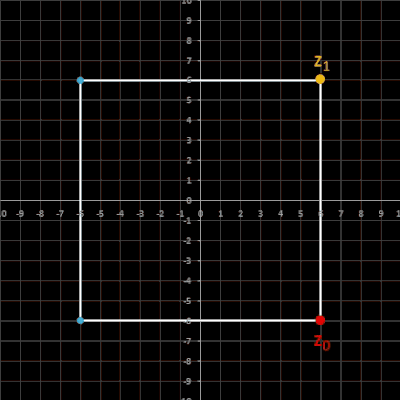
Für bestimmte Startwertkombinationen liefert die Rekursion keine Spiralen, sondern eine zyklische Folge mit λ = 4, deren Folgenglieder ein Quadrat bilden:
• z0 = (a, b) z1 = ( -b, a) a, b ∈ ℝ \ {0}
Quadrat gegenüber der x-Achse bliebig gedreht
z0 = a + i b = a + i b
z1 = g + i d = -b + i a
z2 = a + i (b + 2 g) - 2 d = -a – i b
z3 = i (2 a - 3 d) - 2 b - 3 g = b – i a
z4 = -3 a + i (-3 b - 4 c) + 4 d = a + i b
z5 = i (5 d - 4 a) + 4 b + 5 g = -b + i a
Abschließend und als besonderer Wunsch einer einzelnen Dame und Hundebesitzerin...
Quellenverweise
[1] https://de.wikipedia.org/wiki/Fibonacci-Folge
[3] https://de.wikipedia.org/wiki/Goldener_Schnitt
[4] https://de.wikipedia.org/wiki/Polygon
[5] https://de.wikipedia.org/wiki/Stern_(Geometrie)
[6] https://de.wikipedia.org/wiki/Schl%C3%A4fli-Symbol
[7] https://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Fibonacci/index.html