Integral - Grundlagen
Für eine Funktion f einer reellen Variable x in einem Intervall [a, b] auf der x-Achse ist das bestimmte Integral
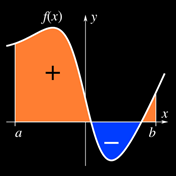
definiert als die vorzeichenbehaftete Fläche der xy-Ebene, die durch den Graphen von f, der x-Achse und den Senkrechten x = a und x = b begrenzt wird. Bei der Berechnung dieser Fläche werden Teilflächen oberhalb der x-Achse addiert, Teilflächen unterhalb der x-Achse subtrahiert.
Der Hauptsatz der Integralrechnung verbindet die Differentiation mit dem bestimmten Integral:
wobei F das unbestimmte Integral ist mit der Eigenschaft F ' (x) = f (x).
Absolute Fläche A
Soll die absolute Fläche A zwischen dem Funktionsgraphen von f und der x-Achse im Intervall [a, b] berechnet werden, wird die Sache etwas aufwendiger, falls f Nullstellen in [a, b] besitzt, da in diesem Fall Teilflächen unter- und oberhalb der x-Achse liegen:
f sei eine Funktion, die im Intervall [a, b] die Nullstellen x1, x2, ..., xn besitzt mit a < x1 < x2 < ... < xn < b.
Für die Berechnung wird das Intervall [a, b] in die Teilintervalle [a, x1] , [x1, x2] , …, [xn,b] zerlegt.
Die absolute Fläche A zwischen dem Graph von f und der x-Achse im Intervall [a, b] beträgt dann
d.h. die absolute Fläche A ergibt sich als Summe absoluter Teilflächen, die getrennt berechnet werden müssen.
Um die Bestimmung der Nullstellen zu vermeiden, kann A auch mit numerischer Integration berechnet werden.
Integral eines Polynoms
Eine Funktion f heißt Polynom, falls sie folgende Struktur aufweist:
wobei die Koeffizienten a0, …, an reelle und die Exponenten natürliche Zahlen sind.
Das unbestimmte Integral F von f ist dann
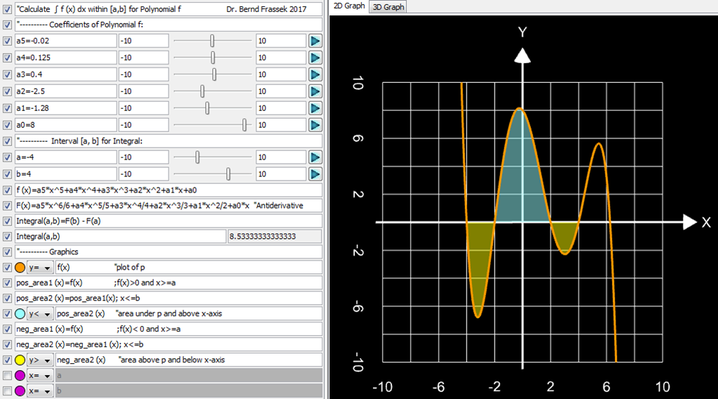
Die Graphing Calculator 3D-Datei Integral of Polynomial.gc3 berechnet das bestimmte Integral im Intervalll
[a, b]:
Die Koeffizienten a0, …, an und das Intervall [a, b] können mit Slidern eingestellt werden.
Teilflächen oberhalb der x-Achse werden in blau, Teilflächen unterhalb der x-Achse in gelb ausgefüllt.
Wichtig: a muss stets kleiner als b sein, da sonst die Einfärbung der Teilflächen nicht funktioniert!
Programmier-Details
- Um die Fläche unterhalb des Graphen und oberhalb der x-Achse farbig zu füllen, wird der Graph Type Regular verwendet mit der Ungleichung "y<" und der Bedingung
f (x) > 0 AND x ≥ a AND x ≤ b
Graphing Calculator 3D erlaubt in einer Bedingung "nur" zwei Ausdrücke, die durch AND / OR verknüpft sind. Daher wird die Bedingung in zwei Zeilen umgesetzt:
pos_area1 (x) = f (x) ;f (x) > 0 and x >= a
pos_area2 (x) = pos_area1(x) ; x <= b
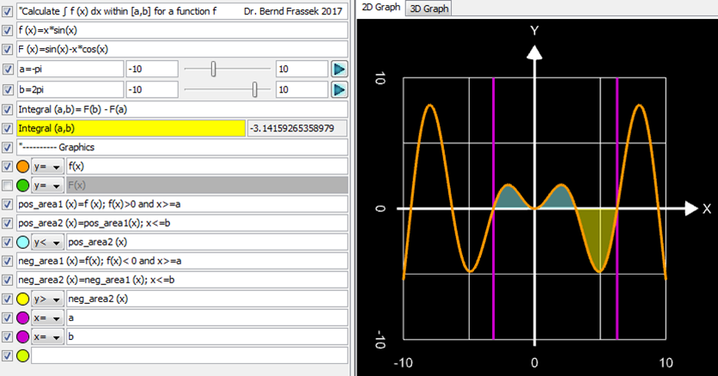
Falls die Stammfunktion F einer Funktion f existiert und bekannt ist [1], kann die GC3D-Datei im letzten Abschnitt vereinfacht werden zu Integral with known Antiderivative.gc3 mit folgenden Einstellungen:
- Die Funktion f wird eingegeben in f(x) = …, z.B. f (x) = x sin(x).
- Die Stammfunktion wird eingegeben in F(x)= … , die für das obige Beispiel lautet sin(x) – x cos(x).
- Das Intervall [a, b] wird mit den Slidern eingestellt.
GC3D ermittelt dann das Integral für das obige Beispiel zu – π.