Doppelintegral
Das Integral einer Funktion mit zwei Variablen f (x, y) über einem Gebiet R in der xy-Ebene heißt Doppelintegral.
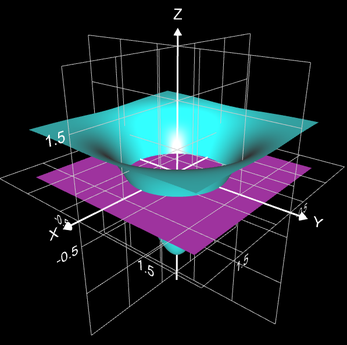
Während das bestimmte Integral einer positiven Funktion f (x) die Fläche zwischen dem Graphen von f und der x-Achse für eine x-Bereich [a, b] darstellt, repräsentiert das Doppelintegral einer positiven Funktion f (x, y) das Volumen zwischen der durch f definierten Oberfläche (im dreidimensionalen Cartesischen System mit z = f (x, y), blauer Bereich) und dem Gebiet R in der xy-Ebene (grauer Bereich).
Für zwei Basistypen von Funktionen wird gezeigt, wie sich dieses Volumen durch Numerische Integration mit Hilfe von Graphing Calculator 3D berechnen lässt.
Doppelintegral Typ 1: f (x, y) = fx (x) • fy (y) + C
Die Funktion f(x, y) enthält zwei Terme fx und fy, die jeweils nur die Variable x bzw. y enthalten und miteinander multipliziert werden, sowie eine additive Konstante C. Hier einige Beispiele:
- f(x, y) = sin(x) cos(y) fx(x) = sin(x) fy(y) = cos(y) C = 0
- f(x, y) = √(1-y²) - 0.5 fx(x) = 1 fy(y) = √(1-y²) C = - 0.5
- f(x, y) = x sin(y) e(-x)+1 fx(x) = x e(-x) fy(y) = sin(y) C = 1
- f(x, y) = sin(x) √(1-y²) x+2 fx(x) = x sin(x) fy(y) = √(1-y²) C= 2
Für diesen Funktionstyp kann das Integral
folgendermaßen berechnet werden:
d.h. fy (y) wird zuerst berechnet (gelbes Integral), danach wird h(x) integriert.
Die obigen Formeln sind in der Graphing Calculator 3D-Datei DInt [fx(x) fy(y) + C] dy dx.gc3 implementiert, mit der die Funktion f(x, y) dargestellt und das Volumen zwischen der Fläche von f und dem Bereich R berechnet werden kann.
Das Beispiel in dieser Datei ist die Funktion f (x, y) = - 2 sin² (x) cos(y) +
2 mit dem Bereich
R = [-2, 2] X [-2, 2], der im Plot violett eingefärbt ist:
Programm-Details:
- Nach der Eingabe der Funktion f (x, y) müssen die Terme fx(x), fy(x) und die Konstante C manuell separiert und eingegeben werden:
f(x,y) = - 2 sin(x)² cos(y) + 2
fx(x) = - 2 sin(x)²
fy(y) = cos(y)
C = 2
- Zum Einstellen von R können die Slider 'a' and 'b' für x und die Slider 'c' und 'd' für y verwendet werden..
- Zum Plotten von f und R kann einfach der Funktionstype '3D Regular' verwendet werden.
Der Nachteil ist bei dieser Wahl jedoch der, dass man den Plot-Bereich für f und R jedes Mal manuell entsprechend der Intervalle [a, b] und [c, d] einstellen muss, sobald man die Intervallgrenzen ändert.
Dies kann man sich ersparen, wenn alternativ der Funktionstyp "Parametric" verwendet wird mit folgender Transformation:
Mit u, v = 0 ... 1 werden so die Intervalle [a, b] und [c, d] erzeugt und die Funktion über dem gewünschten Bereich geplottet.
Die gleiche Transformation für x und y mit z = 0 wird verwendet, um den Bereich R zu plotten.
- Das Ergebnis steht in der Zeile 'Integralx (a,b)'.
- Wichtig: Falls einer der Teilterme fx oder fy in der Funktion fehlt, muss er zu 1 gesetzt werden!
Doppelintegral Typ 2: f (x, y) = fx (x) ± fy (y) + C
Bei diesem Typ werden für die Funktion f(x, y) die beiden Terme fx und fy addiert oder subtrahiert. Falls einer der Terme nicht vorhanden ist, muss er zu Null gesetzt werden.
Für diesen Funktionstyp kann das Integral
folgendermaßen berechnet werden:
Implementiert sind diese Formeln in der Graphing Calculator 3D-Datei DInt [fx(x) + fy(y) + C] dy dx.gc3 die einen 3D-Plot von f (x, y) sowie die Berechnung des Volumens zwischen der Oberfläche von f und dem Bereich R der xy-Ebene liefert.
Das Beispiel in der Datei ist die Funktion f (x, y) = 2x² - y² + 1; das Handling ist das gleiche wie beim Typ 1.
Mit n = 2000 wird der exakte Wert (= 18) mit einem Fehler kleiner als 10-15 berechnet.
Doppelintegral - Beispiele
Das folgende Doppelintegral soll gelöst werden:
Das Integral ist vom "Typ 1"; fx und fy müssen folgendermaßen gesetzt werden:
C = 1
Verglichen mit der exakten Lösung 16 - 3 π erf (2)² berechnet Graphing Calculator 3D mit n = 1000 das Integral mit einem absoluten Fehler von 1.5 • 10-12.
Das folgende Doppelintegral soll gelöst werden:
Das Integral ist vom "Typ 2"; fx und fy werden daher wie folgt gesetzt:
fx (x) = sin (0.2 x²)
fy (y) = cos (0.2 x²)
C = 2
Die exakte Lösung *)
berechnet Graphing Calculator 3D mit mit n = 1000 mit einem absoluten Fehler von 6.26 • 10-10.
*) s. auch Fresnel-Integrale S (x) und C (x)