Shader-B für Polynom mit vorgegebenen Nullstellen
Einen zum Shader-A alternativen Weg zur Darstellung der Basins of Attraction und der Konvergenzgeschwindigkeit beschreiten die Shader-B..., die ich für das Programm VOC programmiert habe (s. unten im Download-Bereich). Hierbei liegt das Polynom jeweils in der Form
vor, d.h. die Nullstellen ζi werden vorgegeben, so dass ohne weitere Berechnungen und Eingaben die Basins of Attraction dargestellt werden können.
• Shader-B1
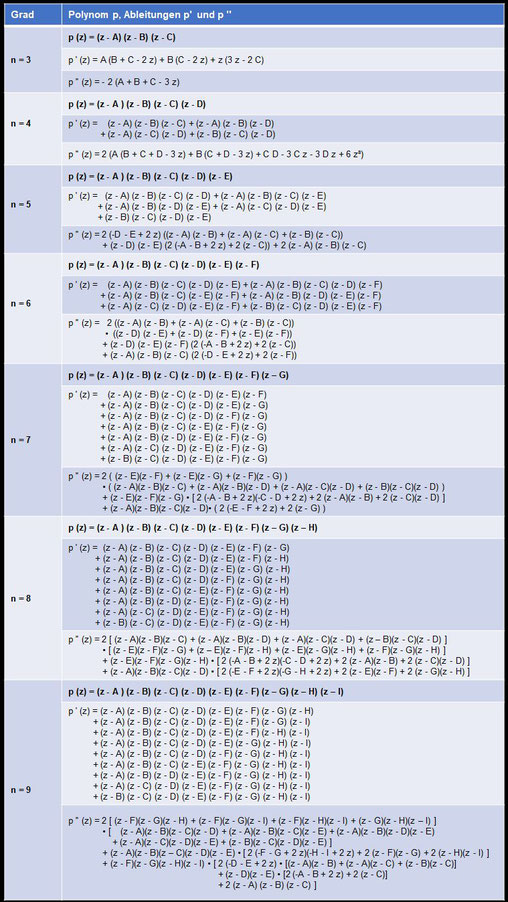
Für das Polynom p mit maximalem Grad n = 9 sowie dessen ausgerechnete Ableitungen p' und p'' (hierbei wurden die Nullstellen ζ1, …, ζ9 in A, ..., I umbenannt) git:
Bei den Verfahren III und IV von Saeed-Aziz sowie bei Hosseini werden auch die dritten Ableitungen p ''' für n = 2 bis n = 9 benötigt, die ich bis dato noch nicht implementiert habe.
Stattdessen habe ich den folgenden Shader programmiert, bei dem für die Berechnung des Polynoms und dessen erste, zweite und dritte Ableitung Rekursionen zugrunde liegen.
• Shader-B2
Für das Polynom pn (z) und die Ableitungen pn' (z), pn'' (z) und pn'' (z) gelten für n ≥ 3 folgende Rekursionen:
pn (z) = pn-1 (z) (z - 𝜁n) p2 (z) = (z - 𝜁2) (z - 𝜁1)
pn' (z) = pn-1' (z) (z - 𝜁n) + pn-1 (z) p2' (z) = 2 z - (𝜁1 + 𝜁2 )
pn'' (z) = pn-1'' (z) (z - 𝜁n) + 2 pn-1' (z) p2'' (z) = 2
pn''' (z) = pn-1''' (z) (z - 𝜁n) + 3 pn-1'' (z) p2''' (z) = 0
Da OpenGL keine Rekursion unterstützt, werden die aufgelösten Rekursionen zunächst für einen maximalen Grad von n = 8 verwendet; hierbei wurden die Nullstellen ζ1, …, ζ8 in A, ..., H umbenannt.
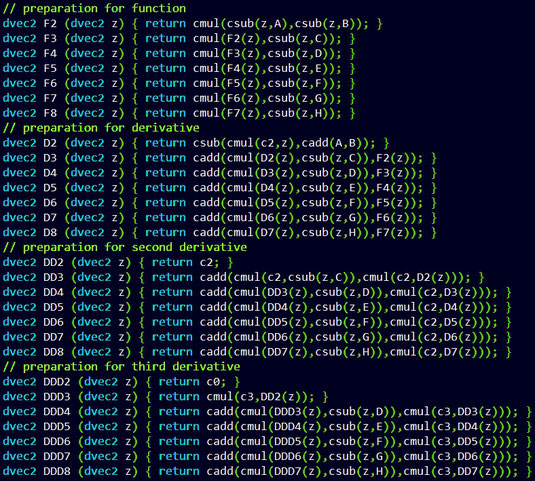
In Abhängigkeit von n gilt dann
- pn (z) = Fn (z)
- pn' (z) = Dn (z)
- pn'' (z) = DDn (z)
- pn''' (z) = DDDn (z).
• Shader-B3
Erweitert man das Schema vom Shader-B2 für einen maximalen Grad von n = 9 mit einer weiteren Nullstelle ζ8 bzw I , so stellt man fest, dass mit der dritten Ableitung p ''' der Shader einfach sang- und klanglos "abstürzt". Man bekommt keinerlei Fehlermeldung - ein sehr großer Nachteil von OpenGL SL. Ich vermute, dass ein zu kleiner Stack für die "rekursiven Aufrufe" das Problem ist.
Eine Version für einen maximalen Grad n = 9 und ohne dritte Ableitung (und natürlich ohne die Verfahren III und IV von Saeed-Aziz und Hosseini) finden Sie als Shader-B3 im Download-Bereich unten auf der Seite.
Möchte man den Shader-B3 für den Grad n = 10 erweitern, so ergibt sich ebenfalls das oben beschriebene Problem.
Die Shader bieten die Möglichkeit der manuellen Vorgabe sowie der zufälligen Berechnung der Nullstellen ζ1, …, ζ9 bzw. A, ..., I. Somit eignen sich die Shader insbesondere auch für "Fraktal-Jäger", die auf der Suche nach interessanten Fraktalen mit minimalen Eingaben sind.
Gesteuert wird die Art der Vorgabe mit der Variablen random_method:
- random_method = 0 : manuelle Vorgabe der Nullstellen
Hier ein Beispiel (Newton-Verfahren) für ein Polynom 5. Grades mit fünf frei gewählten Nullstellen (s. folgende Abbildung):
- random_method = 1 : die Koeffizienten werden mit einem Pseudo Random Number Generator
(kurz: PRNG, s. auch hier) erzeugt.
Die generierten Zufallszahlen randj liegen im Bereich [-1, 1] und werden mit den Faktoren Ri und Ci auf den jeweils gewünschten Bereich der Nullstellen ai expandiert: ζi = (randj • Ri , randj+1 • Ci ).
Die obige Einstellung erzeugt ein zufälliges Polynom 5. Grades mit zwei reellen und drei komplexen Nullstellen (s. Beispiele unten).
Dazu kann für den Startwert Seed des PRNGs eine ganze Zahl im Bereich 0 ... 10 000 000 eingegeben werden, aus der der PRNG dann die pseudo-zufälligen Koeffizienten a0 bis a8 berechnet. Hierzu kann in der Eingabemaske von VOC der Parameter Bailout genutzt werden:
Die eingegebene Zahl (z.B. 47182) erzeugt somit ein Unikat eines Polynoms - es ist der Zahl fest zugeordnet und kann dann für die Untersuchung mit verschiedenen Iterationsverfahren und/oder Einfärbungen genutzt werden, ohne dass beim Klicken auf den OK-Button (Start des Shaders) neue Koeffizienten berechnet werden, wie dies mit random_method = 2 der Fall ist.
Hier dazu einige Beispiele (Halley-Verfahren) mit den obigen Vorgaben für Ri und Ci :
- random_method = 2 : zufällige Erzeugung der Nullstellen bei jedem (!) Shader-Start
mittels Klick auf den OK-Button;
als Startwert für den PRNG wird hier eine von VOC gelieferte Zufallszahl
verwendet.
Die folgenden Animationen zeigen Sequenzen der Basins of Attraction zufällig erzeugter Polynome 5. Grades (links: Newton-, Mitte: Halley-, rechts: Chun III -Verfahren).

Klicken Sie auf ein Bild in der Galerie für eine vergrößerte Darstellung und um sich die Sequenz für ein einzelnes Verfahren besser anschauen zu können.
Download
Für Ihre eigenen Berechnungen / Experimente mit unterschiedlichsten Parametereinstellungen steht hierzu die nachfolgende Datei Rootfind Shader-B.zip als Download zur Verfügung.
Sie enthält den oben beschriebenen Shader-B (CFF-Datei) für das Programm Vision of Chaos und ermöglicht für ca. 50 Iterationsverfahren die Berechnung der Basins of Attraction sowie der Konvergenzgeschwindigkeit für eine komplexe Funktion f : D → ℂ mit D ⊆ ℂ.
Die Datei BFrain.zip, enthält die Palette (MAP-Datei), die auf meinen Webseiten bei der Berechnung und Einfärbung der Konvergenzgeschwindigkeit zugrunde lag (s. dazu Basins of Attraction - Algorithmen) .