Basins of Attraction für Polynom Grad 9 mit einer komplexen Nullstelle

Das Polynom vom Grad 9 entspricht im Aufbau dem Polynom (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4) mit dem Grad 8, jedoch wurde es um die komplexe Nullstelle 2i (weiss) erweitert:

(z+4) (z+3) (z+2) (z+1) (z-1) (z-2) (z-3) (z-4) (z-2i) = 0

Es entspricht dem expandierten Polynom
p (z) = z⁹ - 2 i z⁸ - 30 z⁷ + 60 i z⁶ + 273 z⁵ - 546 i z⁴ - 820 z³ + 1640 i z² + 576 z - 1152 i

Sofern nicht anders angegeben, gilt B = [-4, 4] x [-4, 4].

Klicken Sie bei den folgenden Galerien auf ein Bild für eine größere, detailreichere Ansicht sowie Informationen zum verwendeten Verfahren. Klicken Sie auf die Bildschirmlupe für eine weitere Vergrößerung; mit den Pfeiltasten ← → am linken / rechten Bildschirmrand bewegen Sie sich innerhalb der Galerie.

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Newton-Verfahren

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Schröder-Verfahren

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Behl-Kanwar-Sharma-Verfahren, p=0.2, B=[-9, 10]x[-10, 10]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Behl-Kanwar-Sharma-Verfahren, p=0.8, B=[-15, 15]x[-15, 15]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Basto-Verfahren, B=[-20, 20]x[-20, 20]

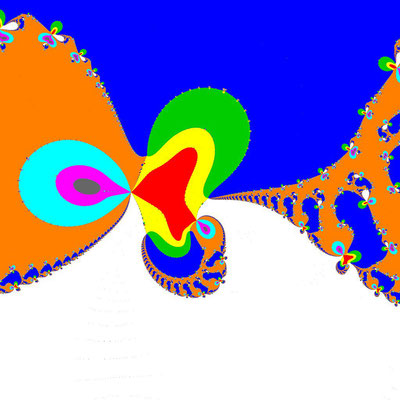
Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Basto-Verfahren, Zoom

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Laguerre-Verfahren, B=[-8, 8]x[-8, 8]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Sekanten-Verfahren, B=[-6, 6]x[-6, 6]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Sekanten-Verfahren, z1=2.6, B=[-7, 7]x[-7, 7]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Sekantenverfahren, z1=7

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Steffensen-Verfahren, beta=-0.00001, B=[-6, 6]x[-6, 6]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ostrowski-Verfahren, B=[-0.5, 0.5]x[0.5, 1.5]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 King-Verfahren, beta=-2.1, Zoom

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Feng-Verfahren, Zoom

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Kung-Traub-Verfahren

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Rafiq-Rafiullah-Verfahren, B=[-2.5, 2.5]x[-2.5, 2.5]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Jarratt-Verfahren, B=[-0.2, 0.2]x[0.9, 1.3]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Bahgat-Verfahren

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Newton-Verfahren, a=1.98

Basins of Attraction (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Chun-Stanica-Neta, B=[-2, 2]x[-2, 2]

Basins of Attraction (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ridders-Verfahren, neg. square root, B=[-10, 10]x[-10, 10]

Basins of Attraction (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ridders-Verfahren, neg. square root, Zoom

Basins of Attraction (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ridders-Verfahren, pos. square root, B=[-10, 10]x[-10, 10]

Basins of Attraction (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ridders-Verfahren, pos. square root, Zoom

Basins of Attraction (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Saaed-Aziz II-Verfahren, B=[-5, 5]x[-5, 5]

Basins of Attraction (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Saaed-Aziz II-Verfahren, Zoom

Basins of Attraction, (z+4)(z+3)(z+2 (z+1 (z-1)(z-2)(z-3)(z-4)(z-2i)=0 Saaed-Aziz III-Verfahren, B=[-1.5, 1.5]x[-1, 2]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Saaed-Aziz IV-Verfahren, neg. Wurzel

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Saaed-Aziz IV-Verfahren, pos. Wurzel

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Saaed-Aziz IV-Verfahren, pos. Wurzel, Zoom

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ghanbari I-Verfahren, B=[-0.5, 0.5]x[-0.5, 0.5]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Thukral-Verfahren, B=[-17, 17]x[-17, 17]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Tiruneh-Verfahren, B=[-11.5, 11.5]x[-11.5, 11.5]

Basins of Attraction (z+4)(z+3)(z+2 (z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ardelean-Verfahren, neg. Wurzel, B=[-2.5, 2.5]x[-2.5, 2.5]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ardelean-Verfahren, neg. Wurzel, Zoom

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Ardelean-Verfahren, pos. Wurzel, B=[-2.5, 2.5]x[-2.5, 2.5]

Basins of Attraction, (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Golbabai-Javidi-Verfahren, Alg. 1, B=[-30, 30]x[-30, 30]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Golbabai-Javidi-Verfahren, Alg. 1, Zoom

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Golbabai-Javidi-Verfahren, Alg. 2, B=[-7, 7]x[-7, 7]

Basins of Attraction (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z-2i)=0 Kou-Li-Liu-He I-Verfahren, B=[-26, 6]x[-15, 17]

Konvergenzgeschwindigkeit (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z+2i)=0 Saaed-Aziz IV-Verfahren neg. Wurzel

Konvergenzgeschwindigkeit (z+4)(z+3)(z+2)(z+1)(z-1)(z-2)(z-3)(z-4)(z+2i)=0 Saaed-Aziz IV-Verfahren neg. Wurzel, Zoom

Weitere Berechnungen / Experimente

Falls Sie die obigen Resultate nachvollziehen oder weitere Berechnungen / Experimente mit unterschiedlichsten Parametereinstellungen vornehmen möchten, steht hierfür die nachfolgende ZIP-Datei als Download zur Verfügung. Sie enthält einen Shader (CFF-Datei), der mit dem Programm Vision of Chaos für die Funktion auf dieser Seite für ca. 50 Iterationsverfahren die Berechnung der Basins of Attraction sowie der Konvergenzgeschwindigkeit (s. dazu Basins of Attraction - Algorithmen) ermöglicht.

Die Datei BFrain.zip, enthält die Palette (MAP-Datei), die auf meinen Webseiten bei der Berechnung und Einfärbung der Konvergenzgeschwindigkeit zugrunde lag (s. dazu Basins of Attraction - Algorithmen).

Rootfind Shader-A p9, 1 komplexe Nullstelle.zip BFrain.zip