Rotationskörper : Volumen bei Rotation um die y-Achse
Für einen Rotationskörper, der durch die Rotation einer Funktion y = f (x) im Intervall [a,b] um die y-Achse entsteht und in der Senkrechten durch f(a) und f(b) begrenzt wird, soll das Volumen bestimmt werden. Hierzu sollen zwei unterschiedliche Vorgehensweisen betrachtet werden.
Hinweis: Für eine Funktion f in Parameterdarstellung siehe unter Volumen mit parametrischer Funktion.
Scheibenmethode (Disc Method)
Bei der Scheibenmethode geht man ähnlich vor wie bei der Volumenbestimmung eines Rotationskörpers, der um die x-Achse rotiert: der Rotationskörper wird hier längs
der y-Achse von y = f(a) bis y = f(b) durch Scheiben der Höhe
∆y angenähert; das genäherte Rotationsvolumen ist dann die Summe der Scheibenvolumina.
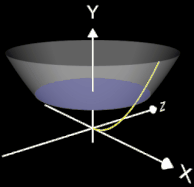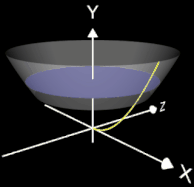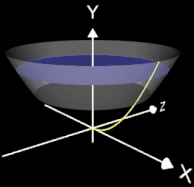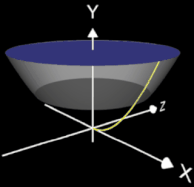
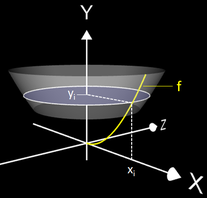
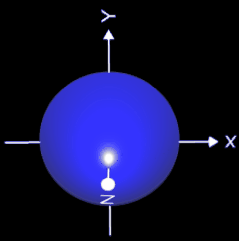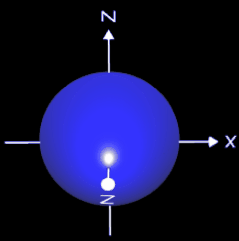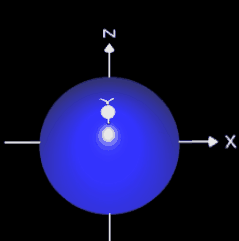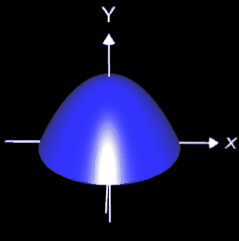
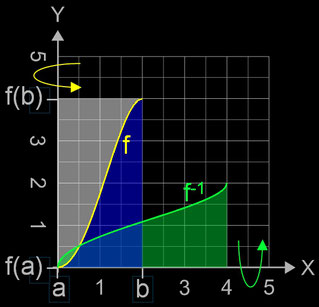
Zur Bestimmung des Volumens der i-ten Scheibe (blau in der Animation) für einen bestimmten yi-Wert benötigt man den dazu zugehörigen Radius xi der Scheibe. Dieser ergibt sich aus der Umkehrfunktion von f:
xi = f -1 (yi).
Somit beträgt das Volumen der i-ten Scheibe
π [ f -1 (yi) ]² ∆y.
Lässt man in einem Grenzwertübergang die Scheiben infinitesimal dünn werden (∆y → 0), so ergibt sich das Volumen Vy des Rotationskörpers zu
Man beachte, dass f stetig und monoton sein muss, damit die Umkehrfunktion existiert.
Mit der Substitutionen xi = f -1 (yi) und dy = f ' (x) • dx erhält man
Dieses Integral lässt sich in der Regel viel leichter lösen, da man zur Funktion f nur deren Ableitung f ' bestimmen muss und die meist recht aufwendige Bestimmung der Umkehrfunktion f -1 sowie deren Stammfunktion entfällt. Die Voraussetzung dafür ist natürlich, dass f ' (insbesondere an den Stellen a und b) existiert (s. Beispiel 2 unten).
Schalenmethode (Shell Method)
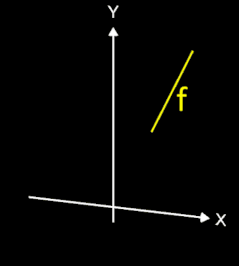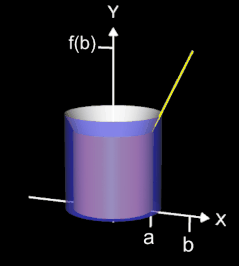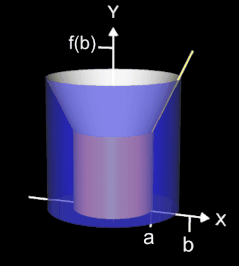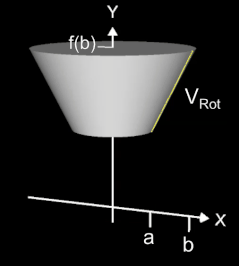
Bei der Schalenmethode wird im Gegensatz zur Scheibenmethode das Volumen durch Integration in x-Richtung gebildet. Unterhalb der Funktion f werden dazu im Intervall [a, b] Schalen (Zylinder) gebildet (blau in Animation rechts). Die Mantelfläche des i-ten Zylinders ergibt sich somit zu 2 π xi f (xi).
Integriert man die Mantelflächen dieser Zylinder im Intervall [a, b], so ergibt sich das Volumen Vs des unterhalb von f liegenden Schalenkörpers
Das endgültige Volumen VRot des Rotationskörpers ergibt sich dann zu
Je nach Lage des rotierenden Funktionsbaschnittes und der Integrationsgrenzen kann das Volumen von
Zyl b oder das Volumen beider Zylinder 0 sein. In letztem Fall sind Scheibenkörper und Rotationskörper
identisch.
Die Graphing Calculator 3D-Datei Solid of Revolution about y-Axis.gc3 plottet einen Rotationskörper mit Rotation um die y-Achse und berechnet dessen Volumen mit beiden oben beschriebenen Methoden (das Volumen und die Darstellung bei Rotation um die x-Achse kann ebenfalls angezeigt werden).
Für die Disc Method muss die Ableitung manuell eingegeben werden, die Integrale werden numerisch gelöst (s. Numerische Integration).
Für die Darstellung des Rotationskörpers bei Rotation um die y-Achse wurde ein "Trick" angewandt
(s. Anhang
unten).
Sektkelch als Rotationskörper um die y-Achse
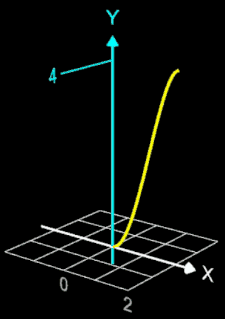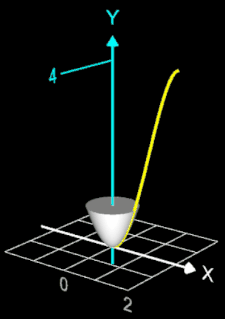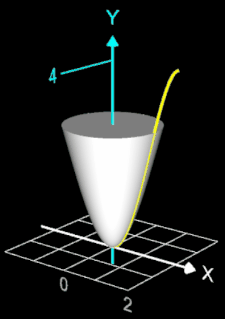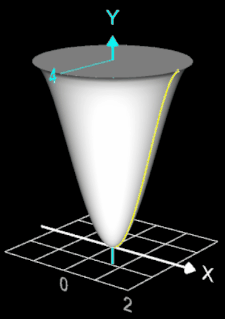
Ein Sektkelchglas kann durch die Rotation der Funktion f (x) = - ¼ x4 + 2 x² um die y-Achse mit x ∈ [0, 2] beschrieben werden. Es soll das Volumen VRot dieses Rotationskörpers bestimmt werden.
Ein Sektkelchglas kann durch die Rotation der Funktion
f (x) = - ¼ x4
+ 2 x² um die y-Achse mit x ∈ [0, 2] beschrieben werden (s. Grafik rechts). Das Volumen VRot dieses Kelches wird im Folgenden
exemplarisch mit drei verschiedenen Methoden bestimmt.
1. Volumenbestimmung mit der Umkehrfunktion
Mittels der Umkehrfunktion
kann die Volumenbestimmung auf den Fall zurückgeführt werden, bei dem der Rotationskörper durch Rotation um die x-Achse entsteht (s. [1]); es ergibt sich:
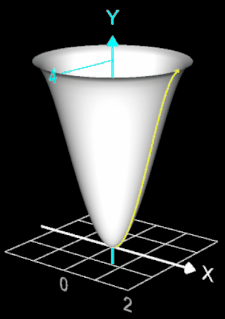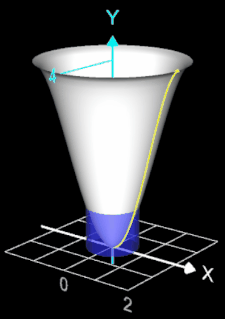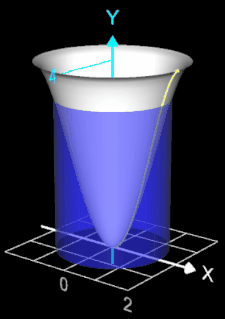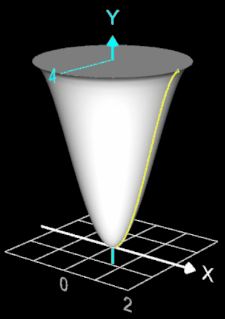
2. Volumenbestimmung mit der Scheibenmethode (Disc Method)
Mit der Ableitung f '(x) = - x³ + 4 x ergibt sich für die Volumenbestimmung (s. auch Animation weiter unten):
Bei numerischer Integration mittels Graphing Calculator 3D
mit
n = 2000 wird eine 12-stellige Genauigkeit erreicht.
3. Volumenbestimmung mit der Schalenmethode (Shell Method)
Bei Anwendung der Shell Method ergibt sich für das Volumen des "Schalenkörpers" (blau in folgender rechter Animation):
Für das gesuchte Volumen VRot muss vom einhüllenden Zylinder Zylb (Radius b = 2, Höhe f(b) = 4) das Volumen des Schalenkörpers subtrahiert werden:
Die numerische Integration mittels Graphing Calculator 3D mit n = 2000 liefert ebenfalls das Ergebnis mit 12-stelliger Genauigkeit.
Kegelstumpf als Rotationskörper um y-Achse
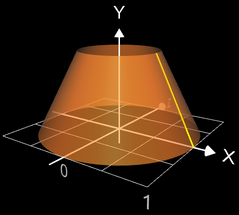
Die Funktion f (x) = - 2 x + 2 mit x aus [0, 1] erzeugt bei Rotation um die y-Achse einen Kegelstumpf.
Aus der Geometrie ist bekannt, dass sich für einen Kegelstumpf mit großem Radius R, kleinem Radius r und der Höhe h das Volumen wie folgt berechnen lässt:
Aus der Funktion f ergeben sich R = 1, r = 0.5 und h = 1; somit beträgt das Volumen
Graphing Calculator 3D liefert mit der Disc Method den gleichen Wert VDisc.
Für die Shell Method liefert Graphing Calculator 3D die Werte Cyl b = 0, Cyl a = 1/4 π, Vs = 1/3 π und somit mit VShell den gleichen Volumenwert.
______________________________________________________
Der volumenmäßig gleiche Kegelstumpf (blau in Grafik) ergibt sich mit der Funktion f (x) = 2 x - 1 im Intervall [0, 1].
Für die Shell Method liefert Graphing Calculator 3D
die Werte
Cyl b = π, Cyl a = 0,
Vs = 5/12 π und somit den gleichen Volumenwert wie beim obigen Kegelstumpf.
Torus als Rotationskörper um die y-Achse
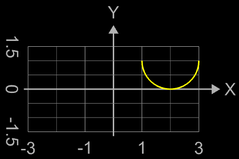
Die Funktion
mit x aus [1, 3] hat die Form eines nach oben geöffneten Halbkreises (s. Grafik rechts) und bildet bei Rotation um die y-Achse einen halben Torus mit den Radien r = 1 und R = 2.
Das Volumen eines Torus (genauer: Kreistorus) beträgt 2 π² R r².
Für den Halbtorus dieses Beispiel ist das Volumen folglich 2 π².
Die in Graphing Calculator 3D realisierte Disc Method lässt sich nicht anwenden, da die Ableitung
an den Stellen x = 1 und x = 3 nicht definiert ist.
Die Shell Method liefert
Cyl b = 9 π, Cyl a
=
π, Vs =
(8-2π)
π und somit 2 π² für den halben Torus.
Backform als Rotationskörper um y-Achse
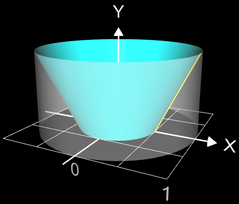
Die Funktion f
(x) = 4 x4 - 4 x² + 1 (gelb in Grafik) bildet im Intervall
[0, 1] bei Rotation um die y-Achse die "Backform" für einen "Gugelhupf".
Die Disc Method liefert mit der Ableitung f
' (x) = 16 x3 - 8 x als Ergebnis für das Volumen 2/3
π, ebenso die Shell Method
mit
Cyl
b = π, Cyl a = 0
und
Vs = 1/3
π.
Für die Darstellung der schönen Riefenstruktur beim fertigen Kuchen und dessen Volumenbestimmung ist Graphing Calculator 3D eher nicht geeignet. Sinnvoller wäre es hier, einen Gugelhupf zu backen und diesen statt einer Volumenbestimmung einem Geschmackstest zu unterziehen ;-)
Guten Appetit!
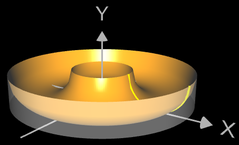
Lochscheibe als Rotationskörper um die y-Achse
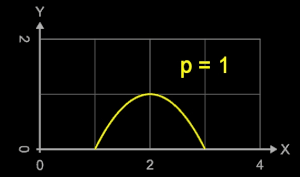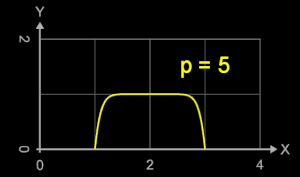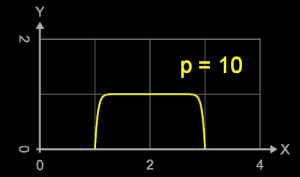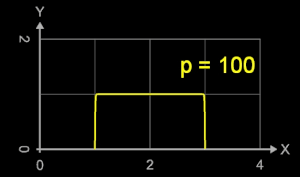
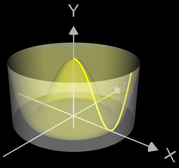
Die Funktion f (x) = - (x - 2)2p + 1 mit p = 1, 2, 3, … im Intervall [1, 3] ist für p = 1 eine nach unten geöffnete Parabel mit
Nullstellen bei x = 1, x = 3 und dem Scheitelpunkt in
(2 | 1).
Mit zunehmenden Werten für p werden die Flanken an den Intervallrändern immer steiler und die Fläche unterhalb des Funktionsgraphen nähert sich
einem Rechteck der Breite 2 und Höhe 1 (s. Animation rechts).
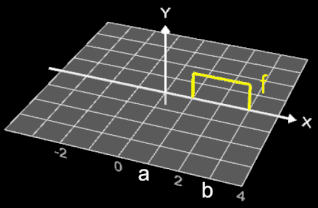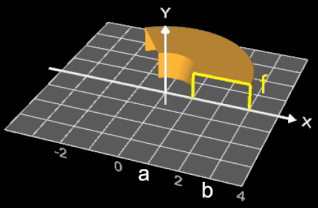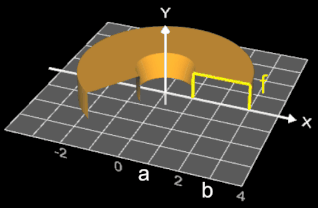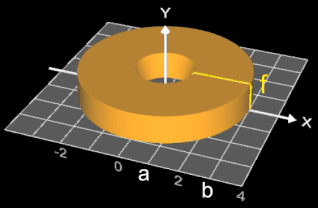
Lässt man f für einen großen Wert von p (z.B. p = 250) um die y-Achse rotieren, so ergibt sich eine "Lochscheibe" mit dem maximalen äußeren Radius 3, dem maximalen Lochradius 1 und der maximalen Höhe 1 als Annäherung an einen Zylinder mit Radius 3, einer Bohrung mit Radius 1 und Höhe 1 (s. Animation rechts).
Das Volumen des Zylinders mit Bohrung beträgt
VZ = 3² π - 1² π = 8 π ≈ 25.1327412287..
Da die Fläche unter f im Intervall [a, b] kein exaktes Rechteck ist, wird das Volumen des Rotationskörpers kleiner sein als das des Zylinders.
Für p = 250 ergibt sich für die Disc und Shell Method der gleiche manuell berechnete Wert von 4000 / 501 π ≈ 25.0825760765.. < 8 π. Bei der Shell Method sind die Volumenwerte von Zyla und Zylb (s. oben) gleich 0.
Die Werte der numerischen Berechnung mit 4000 Iterationen ergeben VDisc = 25.0826098987.. und
VShell = 25.0825760089.. .
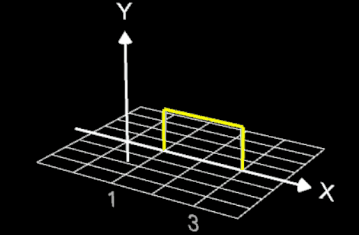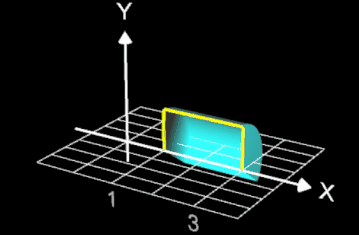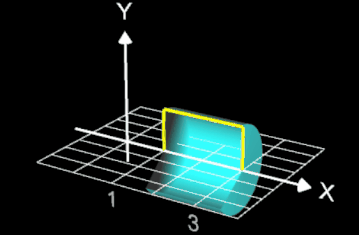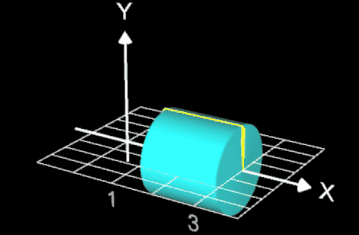
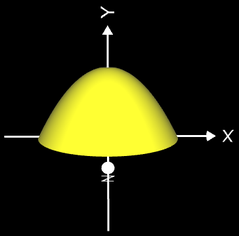
Lässt man die Funktion mit p = 250 um die x-Achse rotieren, so entspricht der Rotationskörper (s. Animation rechts) fast einem Zylinder mit Radius 1 und Höhe 2.
Das Volumen VRot des Rotationskörpers ist etwas kleiner als das des echten Zylinders:
VRot = 6.2643812137.. < 2 π ≈ 6.2831853071..
Anhang: Darstellung der Rotation um die y-Achse
Um die Rotation einer Funktion y = f (x) mit x aus [a, b] um die y-Achse darzustellen, benötigt man die Umkehrfunktion x= f-1 (y) mit y aus [f(a], f(b)].
Ist beispielsweise f (x) = - x² + 1 und das Intervall [a, b] gegeben, kann dies mit Graphing Calculator 3D mittels einer parametrischen Funktion (u = 0 ... 1, v = 0 ... 2π) folgendermaßen realisiert werden:
Die entscheidenden Nachteile sind jedoch ...
- Die Umkehrfunktion zu f muss hergeleitet werden.
- Diese existiert nur dann, falls f stetig und monoton ist (dies ist der Fall für die obige Funktion f ).
- Ggf. muss das Intervall [a, b] in geeignete Abschnitte zerlegt werden, in denen f stetig und monoton ist.
- Wird die y-Achse senkrecht gestellt, sind bei Graphing Calculator 3D nur eingeschränkte Drehbewegungen mit der Maus möglich.
Eine "schnelle, automatische Darstellung" des Rotationskörpers für nicht monotone Funktionen, wie z.B. der "Gugelhupfbackform" (s. Beispiel oben), ist somit nicht möglich.
Daher habe ich folgenden "Trick" angewandt:
- Der Rotationskörper wird mit einer zylindrischen Funktion rund um die z (!) -Achse erzeugt mit
ϕ = 0 ...
2π ;
r durchläuft wegen u = 0 ... 1 alle Werte zwischen a und b,
z alle Funktionswerte von f zwischen a und b:
- Die Bezeichnung (Labels) der y- und z-Achse werden getauscht (s. Animation):
Zwar zeigt die "neue" z-Achse nun in die entgegengesetzte Richtung wie sonst, sie ist aber bezüglich der eigentlichen Aufgabe "Rotationskörper um y-Achse" kaum relevant und wiegt die Vorteile nicht auf:
- Der Rotationskörper um die y-Achse wird "automatisch" erzeugt.
- Es sind alle sonst üblichen Drehungen des Koordinaten-systems mit der Maus möglich.
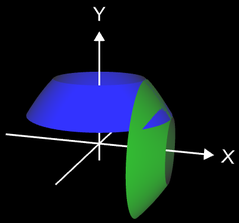
- Beide Rotationskörper (in Grafik: blau für Rotation um y-Achse, grün für Rotation um x-Achse, a = 0.3 und b = 0.8) können problemlos gleichzeitig dargestellt werden.
Download