Rotationskörper : Volumen bei Rotation um die x-Achse
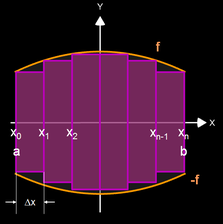
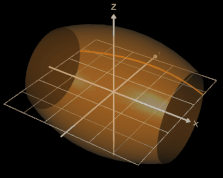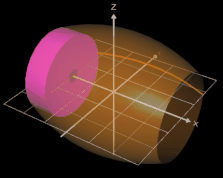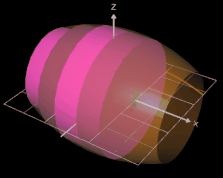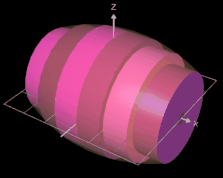
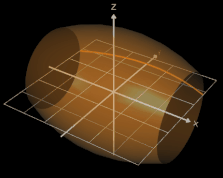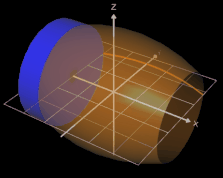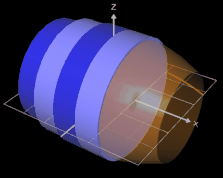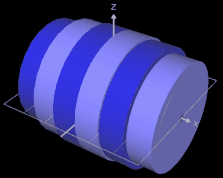
Für einen Rotationskörper, der durch die Rotation einer Funktion y = f (x) um die x-Achse eines Koordinatensystems im Intervall [a, b] entsteht, soll das Volumen bestimmt werden.
Hinweis: Für eine Funktion f in Parameterdarstellung siehe Volumen mit parametrischer Funktion.
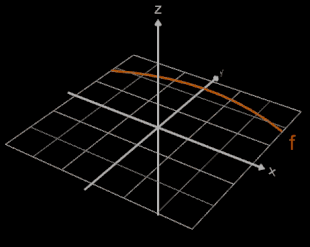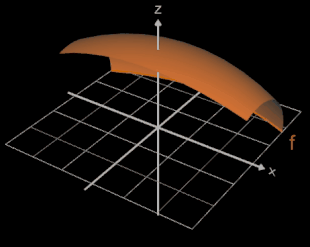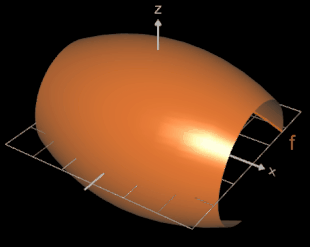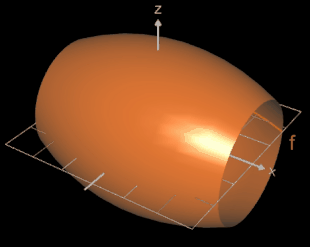
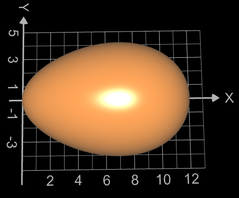
Als Beispiel für die Volumenbestimmung soll ein Fass dienen; dieses entsteht z.B. durch die Rotation (s. oben) der Funktion f (x) = -0.04 x² + 4 um die x-Achse in den Grenzen -5 und 5 (s. Grafik oben).
Kepler'sche Fassformel
Mit diesem Problem beschäftigte sich bereits Johannes Kepler (1571 - 1630) als er für seine Hochzeit Weinfässer bestellte und der Weinhändler mit Hilfe einer Messlatte das Volumen des Weins ermittelte.
"Mir schien es verwunderlich, ob es möglich sei, aus der durch den Körper des halben Fasses quer gezogenen Linie den Inhalt zu bestimmen, und ich zweifelte an der Zuverlässigkeit dieser Messung."
Kepler ermittelte für das Volumen eines Fasses der Höhe h die folgende Näherungsformel:
wobei die Funktion q den Querschnitt an der entsprechende Stelle angibt. Angewandt auf unser Beispiel ergibt sich für das Fassvolumen:
Mit einem tatsächlichen Volumenwert von 425.16 beträgt der Fehler des mit der Kepler'schen Formel ermittelten Volumens lediglich 0.98%.
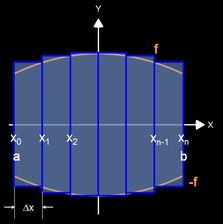
Mit den heutigen Mitteln der Infinitesimalrechnung - Sir Isaac Newton und Gottfried Wilhelm Leibniz sei dank - können wir eine exakte Volumenformel für einen Rotationskörper herleiten. Dazu zerlegen wir das Intervall [a, b] in n gleiche Teile der Breite ∆x und bilden n innen liegende Scheiben (Zylinder):
Das Volumen
Vi der i-ten Scheibe errechnet sich gemäß der Volumenformel für einen Zylinder zu
Vi = π
[ f(xi-1) ] ²
∆x.
Das Gesamtvolumen des durch die innenliegenden Scheiben gebildeten Körpers VI ergibt sich somit zu
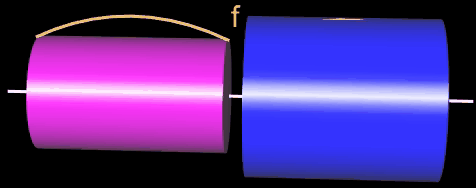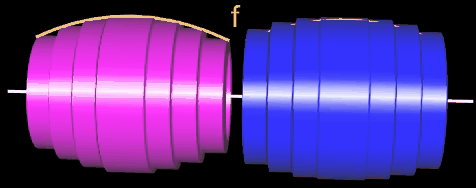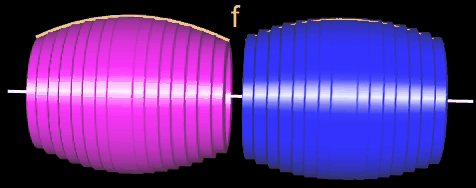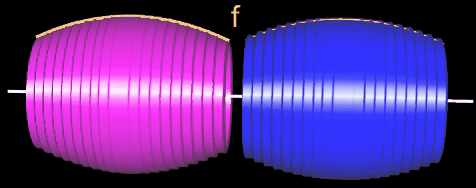
Betrachten wir nun eine Näherung für den Rotationskörper mit n außen liegenden Scheiben:
Das Volumen Vi der i-ten Scheibe beträgt Vi = π [ f(xi) ] ² ∆x. Für den durch die außen liegenden Scheiben gebildeten Körper ergibt sich das Gesamtvolumen VA somit zu
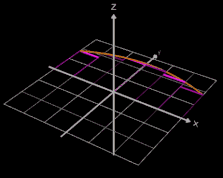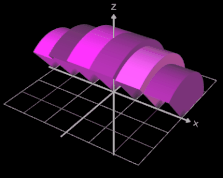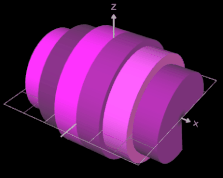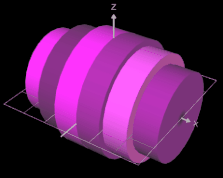
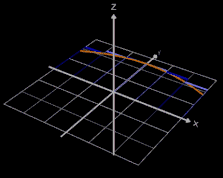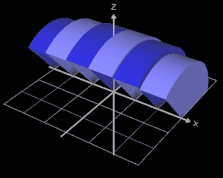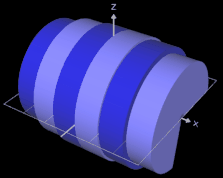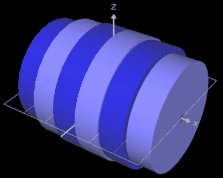
Je größer die Anzahl n der Scheiben ist, desto mehr nähern sich die Konturen der Scheibenkörper der Kontur des durch f erzeugten Rotationskörpers, wie dies in der folgenden Grafik dargestelllt ist:
Für
n → ∞ gehen die Summen in Integrale über - es ergibt sich für beide Scheibenkörper ein gemeinsamer Grenzwert - das Volumen des Rotationskörpers:
Angewandt auf unser Beispielfass ergibt sich mit h (x) = [f (x)]² für das Volumen die folgende Rechnung:
h (x) = [f (x)]² = (- 0.04 x² + 4)² = 0.0016 x4 – 0.32 x² + 16
H (x) = 0.0016 • 1/5 x5 – 0.32 • 1/3 x² + 16 x
H (5) = 203 / 3
H (-5) = - 203 / 3
V = π (203/3 – (- 203/3)) = π • 406/3 = 425.162…
Im folgenden sollen noch weitere Beipiele zur Anwendung der obigen Volumenformel betrachtet werden.
Volumen eines Rotationskörpers mit Wurzel in Randfunktion
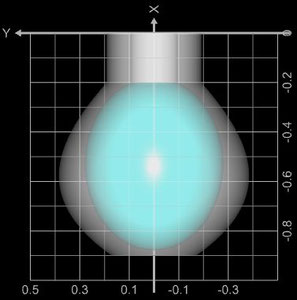
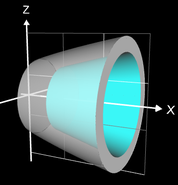
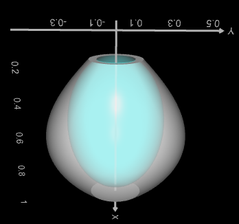
Der Füllraum einer Isolierkanne (blau in nebenstehender Grafik) entsteht durch Rotation der Funktion f um die x-Achse eines Koordinatensystems in den Grenzen - 0.88 bis - 0.2 mit
Hierbei entspricht 1 Zeicheneinheit (ZE) 20 cm. Wie groß ist das Füllvolumen?
mit h (x) = [f (x)] ².
Das Quadrieren von f ist auf Grund der Wurzelfunktion besonders "anwenderfreundlich":
h (x) = 0.8² • (- x² - 1,06 x - 0,1584)
H (x) = 0,64 (- 1/3 x³ - 0,53 x² - 0,1584 x)
H (-0.2) = 0.00841387
H (-0.88) = -0.02808491
V = π (0.00841387 – (-0.02808491)) = 0.11466428 VE
Da 1 VE = (1 ZE) ³ ist, ergibt sich schließlich
V = 0.11466428 • 20³ cm³ = 917.3 cm³
Volumen einer Kugel (Herleitung)
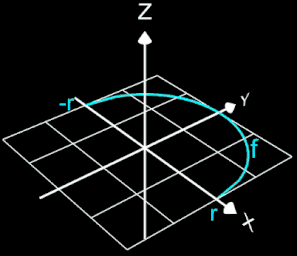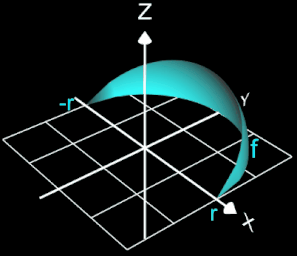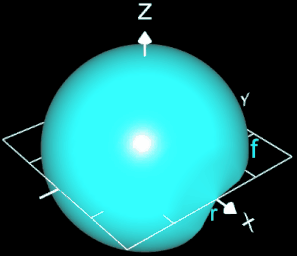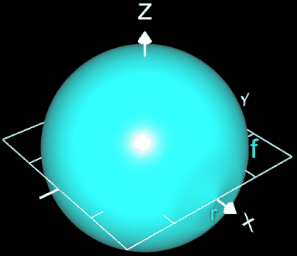
Es soll die Formel zur Volumenbestimmung einer Kugel mit dem Radius r hergeleitet werden.
Die Kugel entsteht durch Rotation der Funktion
um die x-Ache im Intervall [-r, r].
mit h (x) = [f (x)] ² = r² - x²
H (x) = r² • x - 1/3 x³
H (r) = r³ - 1/3 r³
H (-r) = -r³ + 1/3 r³
VKugel = π (r³ - 1/3 r³ + r³ - 1/3 r³) = π • 4/3 r³
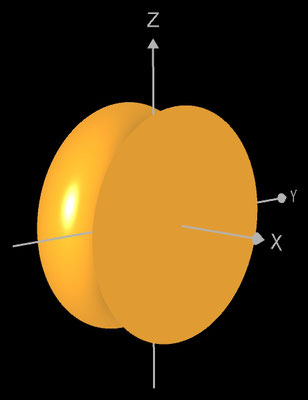
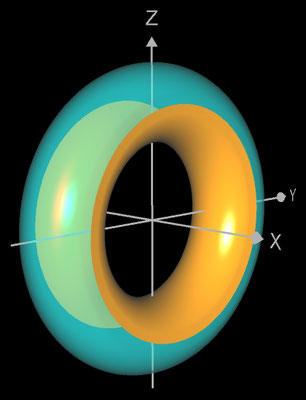
Volumen eines Torus (Herleitung)
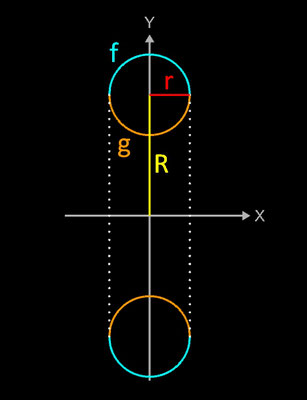
Ein Torus entsteht durch die kreisförmige Rotation mit Radius R eines Kreises mit Radius r um eine Achse.
Ohne Beschränkung der Allgemeinheit möge der Torus durch die Rotation zweier Halbkreise f und g erzeugt werden mit
Somit ergibt sich für das Volumen V des Torus:
Das Integral kann mit partieller Integration wie folgt aufgelöst werden (s. dazu [1] ):
Das Ergebnis 2 π² r² R kann wie oben zerlegt werden und entspricht dann der zweiten Guldin'schen Regel für die Volumenbestimmung von Rotationskörpern, nach der das Volumen eines Rotationskörpers gleich dem Produkt aus Flächeninhalt der erzeugenden Fläche und Umfang desjenigen Kreises ist, der durch die Rotation des Flächenschwerpunktes dieser Fläche erzeugt wird [2].
Die Berechnung des Volumens eines Kreistorus bei Rotation um die y-Achse finden Sie bei Volumen bei Rotation um y-Achse.
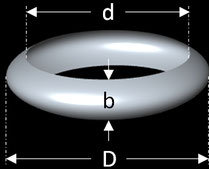
Volumen und Gewicht eines Rings
Für einen Ring aus Platin (s. obere rechte Grafik) mit den folgenden Maßangaben soll das Volumen und Gewicht ermittelt werden:
-
Außendurchmesser D = 2.2 cm
- Innendurchmesser d = 1.7 cm
- Breite b = 5 mm
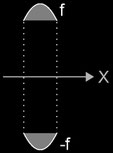
Der Ring ist ein Rotationskörper und entsteht durch Rotation eines Parabelabschnitts um die x-Achse eines Koordinatensystems (s. mittlere Grafik rechts).
Zunächst muss die parabelförmige Funktion f hergeleitet werden. Hierzu muss die Position der y-Achse festgelegt werden. Von den drei Möglichkeiten wählt man zweckmäßigerweise diejenige, bei der die y-Achse durch den Scheitelpunkt des Parabelabschnitts verläuft (s. untere Grafik rechts), da sich so die einfachste Funktion f ergibt mit f (x) = a x² + b:
P1 (-0,25 | 0,85)
P2 (0 | 1,1) Þ c = 1,1
gesucht: x² a + 1,1 = y
0,0625 a + 1,1 = 0,85
0,0625 a = - 0,25
a = - 4 f (x) = - 4 x² + 1,1
Für das äußere Volumen Vf ergibt sich:
mit h (x) = [ f(x) ]²
h (x) = (-4 x² + 1.1)² = 16 x4 – 8.8 x² + 1.21
H (x) = 3.2 x5 – 44/15 x³ + 0.605 x
H (0.25) = 0.26
H (-0.25) = - 0.26
Vf = π [ 0,26 – (-0,26)] = 1.632 VE
Das innere Volumen (Bohrung) ergibt sich zu
VBohrung= π • 0.85² • 0.5 = 1.135 VE.
Das Volumen des Rings beträgt somit:
VRing = 1.632 VE – 1.135 VE = 0.497 VE = 0.497 cm³.
Mit einer Dichte von 21.6 g/cm³ wiegt der Ring 10,744 g.
Volumen und Gewicht doppelwandiger Rotationskörper
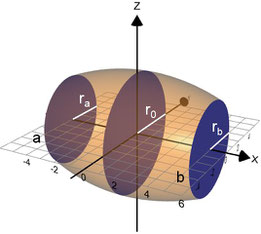
Mit der Graphing Calculator 3D-Datei Solid of Revolution about x-Axis.gc3 lassen sich außer diversen Maßen (s. Grundlagen) auch Volumen V und Gewicht G der Wand eines doppelwandigen Rotationskörpers sowie sein Füllvolumen Vi bestimmen.
Folgende Größen sind hierzu einzugegeben:
- f : äußere Randfunktion
- g : innere Randfunktion
- a , b : Grenzen der äußeren Randfunktion f
- ai , bi : Grenzen der inneren Randfunktion g
- ZE : Zeichen-(Recheneinheit)
-
ρ : Materialdichte der Wand
Berechnet werden:
-
Va :
Außenvolumen (erzeugt durch f)
-
Vi :
Innenvolumen (erzeugt durch g)
-
V : Volumen des Rotationskörpers (Wand)
-
G : Gewicht des Rotationskörpers (Wand)
Die Integrale zur Bestimmung von Va und Vi werden numerisch berechnet (s. Numerische Integration).
Volumen und Gewicht eines Eierbechers
Es sollen Volumen und Gewicht eines Eierbechers aus Glas ermittelt werden. Folgende Größen sind gegeben:
-
f (x) = 1.1 √ (x+2) (äußere Randfunktion)
- g (x) = 0.25 x + 1 (innere Randfunktion)
- Boden bei a = 0.7
- Öffnung bei b = 5
- Innerer Boden bei x = 2
- Glasdichte ρ = 2.2 g/cm³
- 1 Zeicheneinheit ZE = 1 cm
Eingaben: Ergebnisse:
Das Materialvolumen des Eierbechers beträgt ca. 46 cm³, er wiegt ca. 100 Gramm.
Zur Berechnung der Querschnittsfläche des Glaskörpers s. unter Fläche zwischen Funktionen (Beispiel 3).
Volumen und Gewicht eines Hühnereies
Was wäre der schönste Eierbecher ohne ein Ei?
Um ein Ei mathematisch als Rotationskörper zu modellieren, gibt es vielfältige Ansätze (s. dazu auch 3D Ei). Ich habe mich für folgende Wurzelfunktion entschieden, die die Form eines Eies recht gut wiedergibt:
Das Ei liegt im Intervall [0, 6], wobei eine Zeicheneinheit 1 cm beträgt. Als mittlere Dichte für das Ei wird ρ = 1.2 g/cm³ angenommen.
Wie schwer ist das Ei?
Da es nur einen "äußeren Körper" gibt, wird g (x) = 0 gesetzt:
Das Ei wiegt 61 Gramm.
Volumen und Gewicht eines Parfümflacons
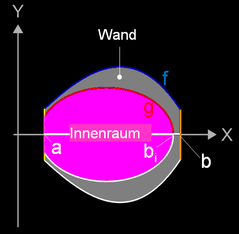
Für einen kleinen Parfümflacon sind das Materialvolumen und das Gewicht zu bestimmen. Der Flacon wird durch die Rotation zweier Funktionen f und g um die x-Achse eines Koordinatensystems erzeugt:
- f (x) = - x³ + x äußere Randfunktion
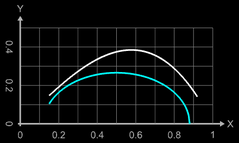
- g(x) = 0.7 √ (- x² + x - 0.1056) innere Randfunkton (blau)
- 1 Zeicheneinheit (ZE) entspricht 8 cm
- der Boden liegt bei x = 0.92, die Öffnung bei x = 0.15
- das verwendete Acrylglas hat eine Dichte von 2.4 g/cm³
Der "Boden" des Füllraums (bi) liegt bei der Nullstelle von g: x = 0.88.
Eingaben:
Ergebnisse:
Das Materialvolumen des Flacons beträgt ca. 63 cm³, sein Gewicht beträgt 150 Gramm.
Quellenverweise
[1] https://www.emathzone.com/tutorials/calculus/integration-of-square-root-of-a2-x2.html
Download