Mantelfläche eines Rotationskörpers
Diese Seite widmet sich der Berechnung der Mantelfläche von Rotationskörpern, die durch die Rotation einer Funktion f um die x- oder y-Achse eines Koordinatensystems entstehen.
Hinweis: Falls f eine parametrische Funktion ist, siehe weiter unten auf der Seite.
Mantelfläche bei Rotation um die x-Achse
Die Mantelfläche M eines Rotationskörpers, der durch Rotation einer Randfunktion f um die x-Achse im x-Intervall [a, b] entsteht, soll bestimmt werden.
Zur Herleitung der Gleichung für M wird der Rotationskörper längs der x-Achse in n Scheiben der Dicke ∆x zerlegt, jedoch nicht wie bei der Herleitung des Rotationsvolumens in zylindrische Scheiben (vgl. Volumen Rotation x-Achse), sondern in Kegelstümpfe, wie in der folgenden Schnittzeichnung dargestellt.

Die Mantelfläche Mn dieses "Scheibenkörpers" ist die Summe der Mantelflächen aller n Kegelstümpfe:
Nach Pythagoras gilt:
Erhöht man die Anzahl n der Kegelstümpfe mit n→∞, so nehmen im Grenzfall die beiden Radien ri und Ri den Wert f (xi) an, die Summe der Mantellinien mi entspricht dann der Länge der Mantellinie des Rotationskörpers (vgl. Länge Funktionsgraph) und es gilt:
Für einige Grundkörper mit aus der Geometrie bekannten Mantelflächen sollen die Berechnungen gemäß der obigen Formel im folgenden beispielhaft durchgeführt werden.
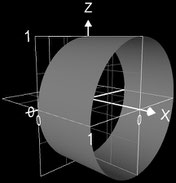
• Mantelfläche Zylinder: M = 2 π r h
mit Radius r = 1 und Höhe h = 1 ergibt sich M = 2 π
per Rotationskörper mit f (x) = 1 und a = 0, b = 1:
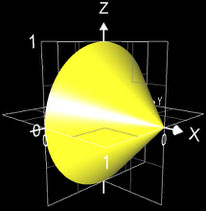
• Mantelfläche Kegel: M = π r s
mit Radius r = 1, Höhe h = 1 und Mantellinie s = √2 ergibt sich M = π √2
per Rotationskörper mit f (x) = 1 - x und a = 0, b = 1:
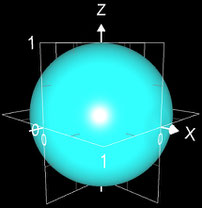
• Mantelfläche Kugel: M = 4 π r²
mit Radius r = 1 ergibt sich M = 4 π
per Rotationskörper mit a = -1, b = 1 und
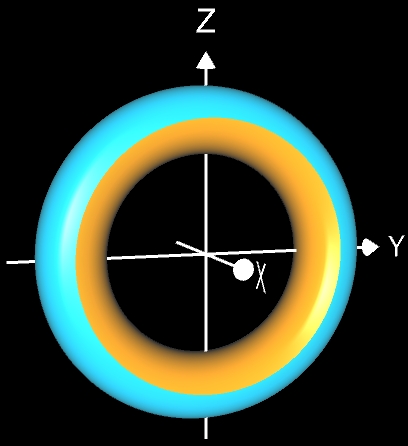
• Mantelfläche Torus: M = 4 π² r R
Der betrachtete Torus entsteht durch Rotation der Funktionsgraphen von f (x) und g(x) um die x-Achse, d.h. durch Rotation der beiden Halbkreise f (x) = R + √ (r² – x²) und g (x) = R – √ (r² – x²) um die x-Achse, wobei f (x) die äußere Mantelfläche Mf und g (x) die innere Mantelfläche Mg bilden (s. Grafiken rechts). DIe Mantelfläche M des Torus ist somit die Summe M = Mf + Mg.
Es ist
und somit
Analog ergibt sich für die innere Mantelfläche Mg = 2 π² r R – 4 π r²
und somit für die gesamte
Mantelfläche
M = Mf + Mg = 4 π² r R
Bei der Berechnung der obigen Mantelflächen sind recht einfache Integrale zu lösen. Abhängig von der Randfunktion können aber auch recht "fiese" Integrale entstehen, deren Lösung sehr aufwendig ist und profunde Kenntnisse und "Tricks" erfordert. Eine Alternative zur manuellen Lösung ist die Anwendung eines CAS (Computer Algebra System), wie z.B. Maxima [2].
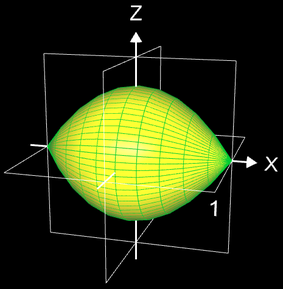
Als Beispiel hierfür diene die "Zitrone", die durch Rotation der recht simplen Randfunktion f (x) = 0.7 (1 - x²) im Intervall [-1, 1] entsteht (s. Abbildung).
Während die Berechnung des Rotationsvolumens recht einfach ist (s. unter Volumen Rotation x-Achse), ergibt sich mit der Abeitung f ' (x) = - 1.4 x = - 7/5 x² folgender Ansatz zur Berechnung der Mantelfläche M:
dessen manuelle Lösung sehr aufwendig ist. Maxima liefert als Stammfunktion hier:
und somit
Einfacher und schneller lässt sich das Integral numerisch berechnen (s. Numerische Integration und diverse Integralanwendugen unter 2D Mathe). Mit dem Graphing Calculator 3D und der gc3-Datei im Download-Bereich unten auf der Seite ergibt sich für n = 2600 in Bruchteilen von Sekunden der gesuchte Wert M = 6.849402255879001:
Oftmals stellt sich auch das Problem, dass überhaupt keine Stammfunktion in geschlossener Form existiert. In diesem Fall ist die numerische Integration der einzige Weg zur Berechnung der Mantelfläche.
Als Beispiel hiefür soll für ein Ei (s. Beispiel 2 unter Volumen Rotation x-Achse) dessen Oberfläche bestimmt werden. Das Ei wird als Rotationskörper durch die Funktion
im x-Intervall [0, 6] erzeugt. Während das Volumen leicht auch "per Hand" berechnet werden kann, ist dies - auch unter Zuhilfenahme eines CAS-Programms - nicht möglich, da zu dem zu lösenden Integral
keine Stammfunktion existiert, so dass man hier auf eine numerische Integration zurückgreifen muss.
Hierbei gibt es noch ein Problem, da an der Eispitze (a = 0) und am Boden (b = 6) die Ableitung f ' nicht definiert ist (Nenner wird 0). Als Abhilfe hierzu nähert man sich den Stellen a und b mittels eines Abstandes δ von rechts bzw. links an. Mit δ = 10-10 ergeben sich die neuen Integralgrenzen zu a = 0 + δ = 0.000 000 000 1 und b = 6 – δ = 5.999 999 999 9 mit dem Ergebnis M = 68.206111962221...
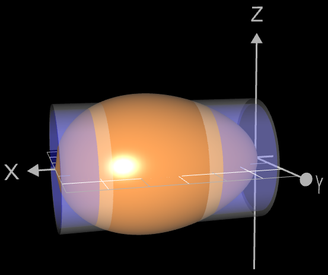
Für das Ei zeigt die nebenstehende Grafik zwei Zylinder mit gleicher Höhe und gleicher Mantelfläche (grau) bzw. gleichem Volumen (blau). DIe Differenz der Radien ist mit 0.16 recht klein, was man zunächst vielleicht nicht vermuten würde.
Möchte man die Aufstellung der Ableitung f ' vermeiden, so kann man diese auch durch den Differenzenquotienten ersetzen (s. Differential):
wodurch sich jedoch die Genauigkeit verringert.
Im Falle des obigen Eies ergibt sich dann eine Differenz zur mit der Ableitung berechneten Mantelfläche von -0.000001797...
Mantelfläche bei Rotation um die y-Achse
Für einen Rotationskörper bei Rotation um die y-Achse ergibt sich entsprechend die Mantelfläche zu
wobei x = f -1(y) die Umkehrfunktion zu f und (f -1(y)) ' deren Ableitung ist.
Das Bilden der Umkehrfunktion lässt sich leider nicht umgehen, wie es bei der Volumenbestimmung bei Rotation um die y-Achse möglich ist. Ist f stetig und streng monoton, so existiert die Umkehrfunktion; ansonsten kann versucht werden, f in
Abschnitte zu zerlegen, in denen f stetig und streng monoton ist, um dann diese Abschnitte getrennt zu berechnen.
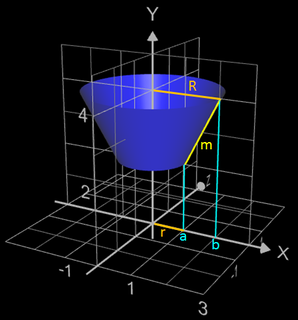
• Mantelfläche eines Kegelstumpfes
Als Beispiel soll die Mantelfläche M eines Kegelstumpfs in der nebenstehenden Grafik bestimmt werden.
Die Mantellinie m wird gebildet durch f (x) = 2x in den Grenzen
a = 1 und b = 2; mit f (a) = 2 und f (b) = 4 beträgt ihre Länge folglich
m = 2 √5. Aus der Geometrie ist bekannt:
M = π (r + R) m = π (1 + 2) • 2 √5 = 6 π √5.
Mit f -1(y) = 0.5 y ergibt sich:
Mantelfläche bei Rotation einer parametrischen Funktion
Ist die rotierende Funktion in parametrischer Darstellung gegeben: x = fx (t), y = fy (t), so ergibt sich die Mantelfläche des Rotationskörpers in den Grenzen x = a und x = b mit
ta = fx-1 (a) tb = fx-1 (b)
Rotation um die x-Achse:
Rotation um die y-Achse:
• Oberfläche einer Kugel
Als einfaches Beispiel hierzu soll die Oberfläche einer Kugel mit dem Radius r und der parametrischen Randfunktion x =
fx (t) = r sin (t) und y =
fy (t) = r cos (t) bestimmt werden. Hierzu wird der Halbkreis zwischen x = - r und x = r um die x-Achse rotiert. Es ist
a = - r = r sin (t) → ta = asin (-1) = - π / 2
b = r = r sin (t) → tb = asin (1) = π / 2
• Oberfläche eines Kugelsegments
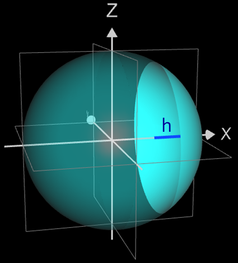
"En passant" kann so auch die Mantelfläche eines Kugelsegments der Höhe h bestimmt werden (s. Grafik). Für die Integralgrenzen
ergibt sich
a = r - h = r sin (t) → ta = asin (1 - h / r)
b = r = r sin (t) → tb = asin (1) = π / 2
und somit für M:
• Mantelfläche einer Zwiebelturmkuppel
Die Rotation der parametrischen Funktion
x = fx (t) = 3 cos4 (t)
y = fy (t) = 5 sin (t) + 1
für t = asin (-0.2) ... π/2 um die y-Achse eines Koordinatensystems erzeugt die typische Kuppel eines Zwiebelturms (s. Animation). Die Mantelfläche M der Zwiebelturmkuppel soll bestimmt werden.
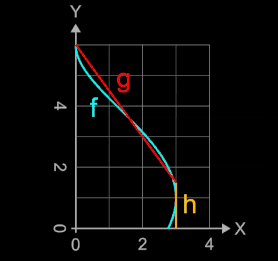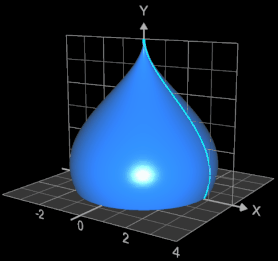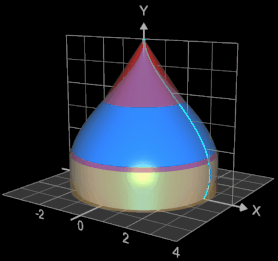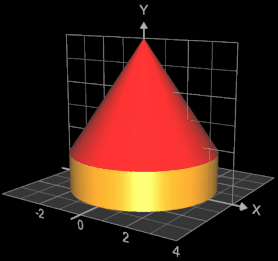
Um zuvor die Mantelfläche abzuschätzen, wird der obere Teil des Dachs durch einen Kegel, erzeugt durch Rotation von g (x) = -1.5 x + 6 um die y-Achse und der untere Teil durch einen Zylinder der Höhe h = 1.5 und dem Radius 3 angenähert. Es ergibt sich für die geschätzte Fläche:
Ma = √(3² + 4.5²) • 3 • π + 3² • π • 1.5 = 79.246..
Mit den Ableitungen
fx' (t) = -12 cos³ (t) sin (t) [ fx' (t) ]² = 144 cos6 (t) sin² (t)
fy' (t) = 5 cos (t) [ fy' (t) ]² = 25 cos² (t)
ergibt sich die Mantelfläche M zu
Da keine Stammfunktion existiert, muss das INtegral numerisch gelöst werden, z.B. mit dem Graphing Calculator 3D:
Für das Zwiebelturmdach wurde auch das Volumen bei [3] sowie die Länge der rotierenden Funktion f bei [4] bestimmt.
Als weiteres Beispiel betrachte man die Funktion
x = fx (t) = t² und y = fy
(t) = t - t³ / 3. In der x/y-Ebene hat ihr Graph die Form eines gestreckten "α" (s. Grafik).
Es soll die Oberfläche des bei Rotation um die x-Achse entstehenden "Tropfens" zwischen
x = 0 und x = 3 bestimmt werden:
ta = 0 tb = √3
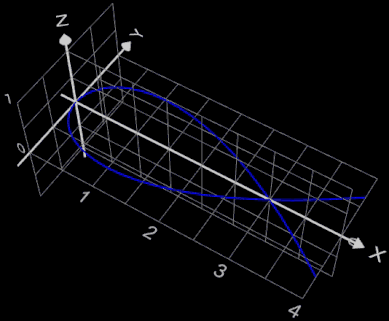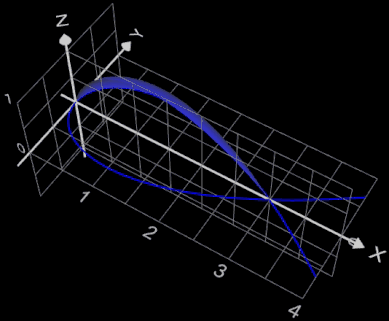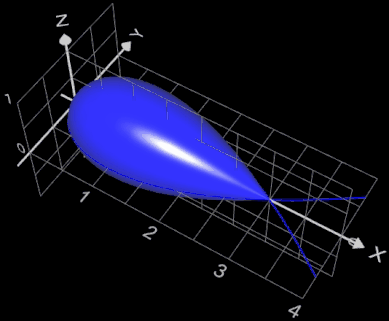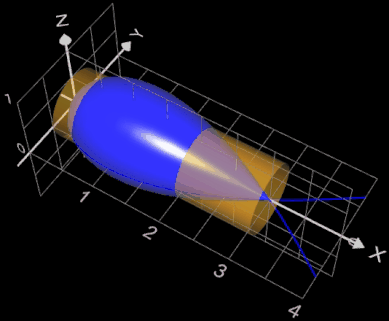
Der braune, transparente Zylinder in der Grafik besitzt bei gleicher "Länge" (b - a = 3) die identische Mantelfläche. Er hat mit seinem Radius von 0.5 die gleichen
Maße wie der Zylinder mit gleichem Volumen wie das des Rotationskörpers um die x-Achse (s. auch Volumen mit parametrischer
Funktion).
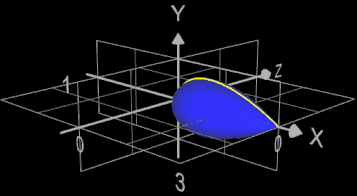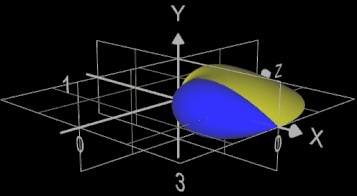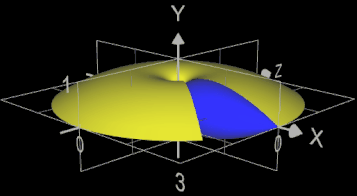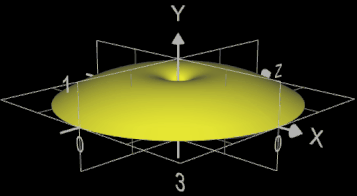
Bei Rotation der vorigen Funktion um die y-Achse ergibt sich für die Mantelfläche des entstehenden Rotationskörpers (gelb in nebenstehender Grafik):
Quellenverweise
[1] Singh, Ravish R, (1993), Engineering Mathematics (6th ed.), Tata McGraw-Hill, S. 6.90
[2] https://maxima.sourceforge.io/de/index.html
[3] https://www.frassek.org/3d-mathe/rotationsk%C3%B6rper/volumen-mit-parametrischer-funktion/
[4] https://www.frassek.org/2d-mathe/l%C3%A4nge-funktionsgraph/
Download