Rotationskörper - Grundlagen
In der Mathematik, im Ingenieurwesen und der Fabrikation versteht man unter einem Rotattionskörper ein räumliches Objekt, dessen Oberfläche durch Rotation einer erzeugenden Kurve (Funktion f) um eine Rotationsachse gebildet wird. Die erzeugende Kurve liegt dabei in der gleichen Ebene wie die Rotationsachse.
Bekannte Rotationskörper sind z.B. Zylinder, Kegel, Kegelstumpf, Kugel und Torus.
Für die Rotationskörper auf meiner Webseite ist die erzeugende Kurve der Graph einer Funktion y = f (x) innerhalb eines x-Intervalls [a, b]. Diese nennt man üblicherweise auch Randfunktion, da sie den Rand und somit die Oberfläche des Rotationskörpers beschreibt.
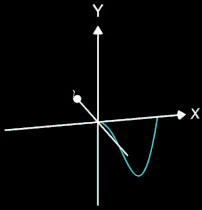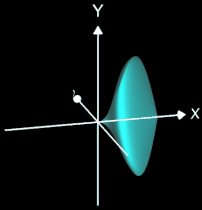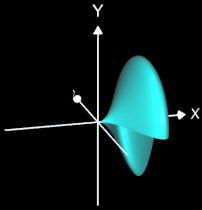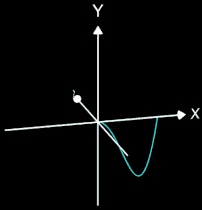
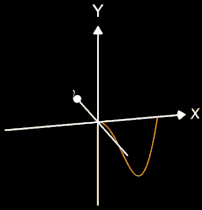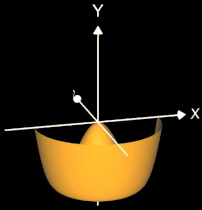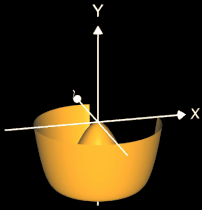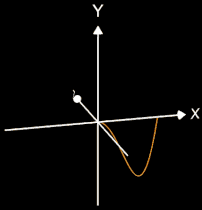
Da die Rotationsachse in der gleichen Ebene wie die erzeugende Kurve (Funktion) liegen muss (also in der x/y-Ebene), kommt hierfür entweder die x-Achse oder die y-Achse in Betracht, wobei die entstehenden Rotationskörper bei gleichen Randfunktion f in der Regel sehr unterschiedlich aussehen, wie das Beispiel in beiden folgenden Grafiken zeigt:
Der 3D-Plot eines Rotationskörpers mit einer allgemeinen Randfunktion f wird mit einer parametrischen Funktion mit den Parametern u und v erzeugt:
Rotation um x-Achse:
x (u) = u
y (u, v) = f (u) • cos (v)
z (u, v) = f (u) • sin (v)
u = a … b
v = 0 … 2π
Rotation um y-Achse:
x (u) = f-1 (u) • cos (v)
y (u, v) = u
z (u, v) = f-1 (u) • sin (v)
u = f (a) … f (b)
v = 0 … 2π
f-1 ist die Umkehrfunktion zu f
Geht es lediglich um einen 3D-Plot der Rotation um die y-Achse, so ist das Bilden der Umkehrfunktion f-1 nicht erforderlich, da man einfach die Achsen vertauschen kann (s. Anhang bei Volumen bei Rotation um y-Achse).
Modellierung realer Objekte als Rotationskörper
Einige reale Objekte aus dem Alltag lassen sich als Rotationskörper modellieren (s. auch Beispiele), wobei in einem geeigneten Koordinatensystem die waagerechte x-Achse oder die senkrechte y-Achse als Rotationsachse dienen.
Viele dieser Objekte, wie z.B. Gläser, Flaschen, Behälter stehen "senkrecht" auf einer Unterlage und entstehen eigentlich durch die Rotation einer erzeugenden Kurve um die y-Achse. Meist ist es, insbesondere wenn Volumen oder Mantelfläche des Rotationskörpers brechnet werden sollen, viel einfacher und weniger aufwendig, die x-Achse als Rotationsachse bei der Modellierung zu verwenden!
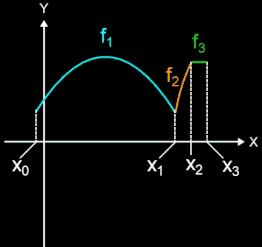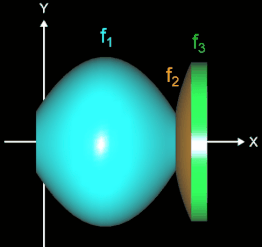
Die Rotation um die x-Achse bietet sich vor allem dann an, wenn das Objekt längs der Rotationsache nicht durch eine einzige Funktion f sondern vielmehr durch verschiedene Teilfunktionen f1, f2,…, fn beschrieben werden kann (s. Animation rechts).
Das Volumen Vrot eines solchen Objekts bei Rotation um die x-Achse ergibt sich dann zu:
Aber auch dann, wenn der Rotationskörper durch Rotation nur einer einzigen Randfunktion f um die x-Achse erzeugt werden kann, ist die Erzeugung dieses Körpers durch Rotation der
Umkehrfunktion f-1
um die y-Achse in der
Regel recht aufwendig.
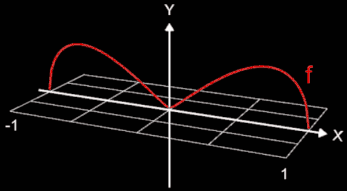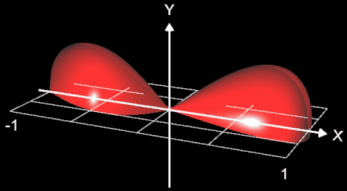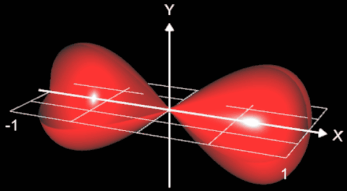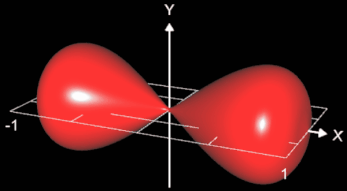
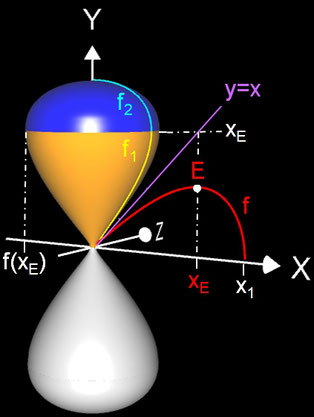
Dies soll anhand einer Sanduhr (s. nebenstehende Grafik) verdeutlicht werden. Für diese soll das Volumen bestimmt werden, wobei aus Symmetriegründen nur eine Hälfte dazu verwendet wird.
Bei der Rotation um die x-Achse (s. folgende Animation) lässt sich die Sanduhr durch die Funktion
für x ∈
[-1, 1] beschreiben .
Für das Volumen einer Hälfte (positive x-Werte) ergibt sich mit der Nullstelle x1 von f1 das Integral
das sich manuell mit Hilfe der Potenzregel einfach lösen lässt:
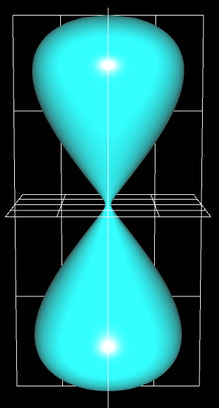
Nun soll diese Sanduhr durch
Rotation der Umkehrfunktion f-1 von f um die y-Achse erzeugt werden. Da f aber im relevanten Intervall nicht streng monoton ist (f hat einen
Extremwert bei xE), existiert für dieses keine Umkehrfunktion. Teilt man das Intervall jedoch in die beiden Teilintervalle
[0, xE] und [xE, x1], so existieren für diese die zwei Umkehrfunktionen für die Rotation um die y-Achse:
Für die Berechnung des Volumens bei Rotation um die y-Achse z.B. mit der Schalen-Methode (Shell Method) sind folgende zwei Integrale zu lösen:
Dies erfordert deutlich mehr Aufwand als bei der Rotation um die x-Achse. Einfacher ist die Lösung mit einem CAS (Computer-Algebra-System) oder die numerische Lösung.
Berechnungen an doppelwandigen Rotationskörpern
Wie oben bereits erwähnt, lassen sich viele Objekte aus dem Alltag idealerweise durch Rotation einer Funktion um die x-Achse modellieren. Da solche "echten" Objekte eine Wand mit einer entsprechenden Wanddicke besitzen, benötigt man eine zweite Randfunktion für die Rotation um die x-Achse. Die Wand befindet sich somit zwischen der äußeren und der inneren Randfunktion.
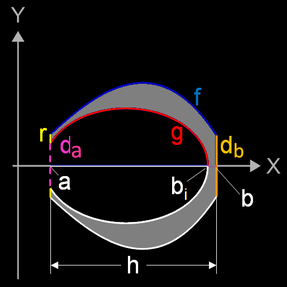
In der Graphing Caculator 3D-Datei Solid of Revolution about x-Axis.gc3 ist dies berücksichtigt. Sie erzeugt einen Rotationskörper mit Wand (grau in folgender Querschnittskizze) und liefert diverse Maße ebenso wie die Volumina der Wand und des Innenraums (s. hierzu Volumen Rotation um x-Achse):
Folgende Größen können hierbei eingegeben werden:
- f : äußere Randfunktion
- g : innere Randfunktion
- a , b : Grenzen der äußeren Randfunktion f
- ai , bi : Grenzen der inneren Randfunktion g
- ZE : Zeichen-(Recheneinheit)
Berechnet werden:
- h : Höhe des Rotationskörpers
-
da
: Durchmesser der Öffnung bei a
-
db
: Bodendurchmesser bei b
- r : Breite des Randes an der Öffnung
In der Grafik ist a = ai gewählt, da der Rotationskörper sonst keine Öffnung hätte.Selbstverständlich lassen sich a und b und somit die Position des Bodens und der Öffnung vertauschen.
Weiterhin kann man durch Anklicken wählen, ob der Rotationskörper am Boden oder der Öffnung offen sein soll, einen geschlossenen "Deckel" oder einen Deckel mit Öffnung entsprechend der dortigen Wanddicke r besitzen soll:
Außerdem kann man mittels eines Sliders ("t") den Winkel der Rotation von 0 (nur die Randfunktionen) bis 1 (geschlossene Mantelfläche des Rotationskörpers) einstellen bzw. animieren (s. oben).
Beispiele für die Berechnung obiger Maße an
Rotationskörpern um die x-Achse finden Sie unter
Volumen bei Rotation um x-Achse, wobei die Graphing Calculator 3D-Datei auch
noch das Volumen und Gewicht des Rotationskörpers berechnet.
Download