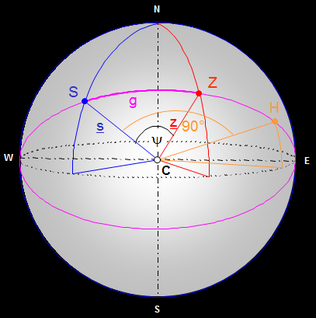
Orthodrome (Großkreis)

In der Ebene ist die kürzeste Verbindung zweier Punkte ein Streckenabschnitt auf einer Geraden.
Auf einer Kugel ist die kürzeste Verbindung zweier Punkte ein Teilstück einer Orthodrome. (griech. orthos für "gerade", dromos für "Lauf"). Eine solche Orthodrome (auch Großkreis) G auf einer Kugel mit dem Radius rS ist ein Kreis mit folgenden Eigenschaften (s. Abbildung):
-
sein Radius rG ist gleich dem Kugelradius rs
- sein Mittelpunkt liegt im Kugelmittelpunkt C.
Ein Schnitt auf dem Großkreis teilt die Kugel in zwei Hälften. Es gibt unendlich viele Großkreise auf der Kugel. Alle
Längenkreise (Meridiane) [1] sind Orthodrome. Bis auf den Äquator sind aber alle Breitengrade B [2] keine
Großkreise; ihr Radius rB ist stets kleiner
als der Kugelradius rs.
Berechnung der Bogenlänge g auf der Orthodrome
Die Bogenlänge g auf der Orthodrome zwischen den Punkten S und Z, gemeinhin auch als "Luftlinie" bezeichnet (s. folgende linke Grafik), soll im Folgenden bestimmt werden.
Die Bogenlänge g zwischen den Punkten S und Z auf der Orthodrome entspricht dem Winkel ψ zwischen den Vektoren s und z (s.
obige rechte Grafik). Mit Hilfe des Skalarprodukts s • z = xs xz + ys yz + zs zz ergibt sich mit r = | s | = | z | = 1 für den Winkel Ψ:
Ψ = arccos (xs xz + ys yz + zs zz)
(2)
Die Bogenlänge g errechnet sich für den mittleren Erdradius rs = 6371 somit zu
Beispielsweise ergibt sich für die Entfernung von Amsterdam nach San Francisco eine Länge von 8783 km.
Berechnung eines Punkts auf der Orthodrome
Zur Berechnung eines beliebigen Punktes auf der Orthodrome durch S und Z in einem Kartesischen Koordinatensystem ist ein weiterer Hilfspunkt H auf der Orthodrome erforderlich, der vom Punkt S ausgehend 90° entfernt in Richtung Z liegt (s. obige rechte Grafik).
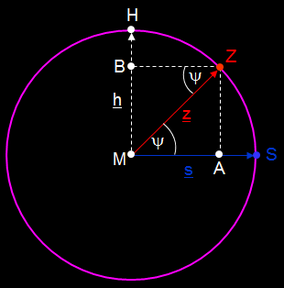
Um die Koordinaten von H zu ermitteln, ist es hilfreich, senkrecht auf die Orthodrome zu blicken, wie dies in der nebenstehenden Grafik dargestellt ist. Dabei kommen folgende Größen ins Spiel:
s : Vektor von M nach S
z : Vektor von M nach Z
h : Vektor von M nach H
MA : Vektor von M nach A
AZ : Vektor von A nach Z
MB : Vektor von M nach B
Gesucht ist der Vektor h. Die Projektion von z auf s ergibt zunächst MA = s cos (Ψ) und es gilt
AZ = z – MA = z - s cos (Ψ)
Somit ergibt sich für die Koordinaten von H:

Für die Berechnung eines beliebigen Punktes G auf der Orthodrome in einem Winkelabstand von γ ergibt sich dann gemäß nebenstehender Abbildung
g = MA + MB = s cos (γ) + h sin(γ)
mit g als Vektor von M nach G. Die Koordinaten von G lauten demnach:
yG = ys cos (γ) + yH sin (γ) (5)
zG = zs cos (γ) + zH sin (γ)
Durchläuft γ den Bereich von 0° bis 360°, so ergibt sich die vollständige Orthodrome.
Anmerkung: Die Berechnung der Koordinaten von G kann auch ohne den Hilfspunkt H erfolgen gemäß:
xG = xS cos (γ) + sin (γ) (xZ - xS cos (Ψ)) / sin (Ψ)
xG sin (Ψ) = xS cos (γ) sin (Ψ) + xZ sin (γ) - xS cos (Ψ) sin (γ)
= xS (cos (γ) sin (Ψ) - cos (Ψ) sin (γ) ) + xZ sin (γ)
= xS sin (Ψ - γ) + xZ sin (γ)
xG = (xS sin (Ψ - γ) + xZ sin (γ)) / sin (Ψ)
(für y und z entsprechend), jedoch wird H auch für weitere Berechnungen am Großkreis (s.u) benötigt.
Die Länge λG und Breite φG des Punktes G lässt sich aus den kartesischen Koordinaten berechnen gemäß
λG = arcsin (z)
φG =
arctan (y /
x)
(6)
In EXCEL wird die letzte Gleichung mittels der Funktion "ATAN2 (y;x)" berechnet, da diese Funktion auch für den x-Wert Null definiert ist.
Berechnung des nördlichsten und südlichsten Punktes der Orthodrome
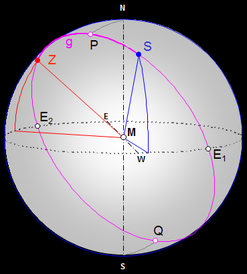
Für die Kurseermittlung ist zunächst die Berechnung des nördlichsten Punktes P bzw. südlichsten Punktes Q auf der Orthodrome erforderlich (s. folgende Grafik).

Für den nördlichsten Punkt P gilt, dass seine z-Koordinate das Maximum aller z-Koordinaten der Punkte auf der Orthodrome ist. Nach Gleichung (5) gilt für die z-Koordinate von P:
zp = zs cos (φp) + zH sin (φp)
Mit der notwendigen Bedingung für das Maximum (dz / dφp = 0) ergibt sich
dz / dφp = - zs sin (φp) + zH cos (φp) = 0zH / zs = sin (φp) / cos (φp) = tan (φp)
φp = arctan (zH / zs) φQ =
φp + 180°
Für die Koordinaten von P gilt nach Gleichung (5) schließlich:
xp = xs cos (φp) + xH sin (φp)
yp = ys cos (φp) + yH sin (φp)
zp = zs cos (φp) + zH sin (φp)
Berechnung des Start- und Zielkurses
Möchte man sich längs des Bogens g der Orthodrome in der voranstehenden Grafik bewegen - g stellt die kürzeste Verbindung von Amsterdam (S) und San Francisco (Z) dar - so stellt man fest, dass man ausgehend vom Startpunkt Amsterdam zunächst einen nördlichen Kurs α Richtung Westen einschlagen muss, dann aber in einem südlichen Kurs ω ankommt:
Tatsächlich muss man den Kurs auf der Orthodrome kontinuierlich anpassen, wenn man im Zielpunkt Z ankommen möchte. Bewegt man sich hingegen auf einer Loxodrome (s.u.), so ist dies nicht erforderlich - ein großer Vorteil - jedoch sei hier vorwegnehmend angemerkt, dass der Weg auf der Loxodrome in den meisten Fällen deutlich länger ist.
Zur Berechnung von Start- und Zielkurs müssen zunächst die Winkel α' und ω' (s. folgende Grafik) gemäß dem Seitenkosinussatz für sphärische Dreiecke [3] ermittelt werden.
Startkurs α
Zur Bestimmung des "echten" Startkurses α sind 2 Parameter entscheidend:
- die längenmäßige Richtung (links : westlich, rechts : östlich) des Bogens von S nach Z
- die längenmäßige Lage des nördlichsten Punkts P bezüglich des Startpunktes S.
Die Fälle λS = λZ unter Punkt 1 und λS = λP unter Punkt 2 sind Sonderfälle (s.u.).
Da λ im Bereich von –180° bis 180° liegen kann, ergibt sich für die Richtungsbestimmung folgende Fallunterscheidung mit ∆λ =
λS – λZ :
|
Bedingungen |
Bogenrichtung SZ |
|
λS < λZ , -180° < ∆λ λS > λZ , 180° < ∆λ < 360° λS < λZ , -180° < ∆λ < 0° |
rechts |
|
| ∆λ | = 180° |
vertikal |
|
sonst |
links |
Die Lagebestimmung von P bezüglich S erfolgt nach dem gleichen Schema mit ∆λSP = λS - λP :
|
Bedingungen |
Lage von P bzgl. S |
|
λS < λP , -180° < ∆λSP λS > λP , 180° < ∆λSP < 360° λS < λP , -180° < ∆λSP < 0° |
rechts |
|
| ∆λ | = 180° |
identisch |
|
sonst |
links |
Der "echte" Kurswinkel αOrtho errechnet sich dann gemäß
|
Bedingungen |
α |
|
|
λP < λS |
Richtung: rechts |
180° - α' |
|
Richtung: links |
360° + α' |
|
|
λP = λS |
Sonderfall (s.u.) |
|
|
λP > λS |
Richtung: rechts |
α' |
|
Richtung: links |
180° - α' |
|
Zielkurs ω
Die Bestimmung des "echten" Zielkurses ω erfolgt nach den gleichen voranstehenden Überlegungen, wobei sinngemäß P durch Z und α durch ω ersetzt wird.
Sonderfälle bei der Kursberechnung
Für einige wenige Kombinationen von S und Z versagt die Berechnung nach den obigen Gleichungen. Liegen z.B. S und Z auf dem Äquator, ist die Bestimmung von P und Q nicht möglich; liegen S und Z auf dem gleichen Meridian, müssen die Breiten φS und φZ berücksichtigt werden, um den kürzesten Bogen g zwischen S und Z zu bestimmen.
Schnittpunkte der Orthodrome mit dem Äquator
Jeder Großkreis außer dem Äquator selbst schneidet den Äquator in zwei Punkten E1 und E2 (s. folgende Abbildung). Die Längen dieser Punkte sind 90° entfernt vom nördlichsten Punkt P bzw. südlichsten Punkt Q. Die Berechnung der Koordinaten von E1 und E2 erfolgt gemäß der Gleichungen (5) und (6).
Kursbeispiele für die Orthodrome
Kursbeispiele mit verschiedenen Kombinationen von Startpunkt S und Zielpunkt Z sowie dem alternativen Weg auf der Loxodrome finden Sie unter Kursbeispiele.