3D Spiralen
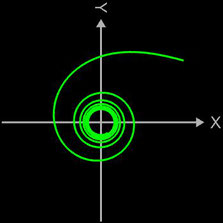
Als Spiralen im engeren Sinn bezeichnet man in der Mathematik ebene Kurven, die aus unendlichen vielen Windungen um einen festen Punkt bestehen und aus höchstens zwei Ästen mit streng monotonem
Zusammenhang zwischen Drehwinkel und Radius zusammengesetzt sind. Sie kommen in der Natur, der
Technik, der Architektur und Kunst praktisch jedes Kulturkreises und jeder Epoche vor [1].
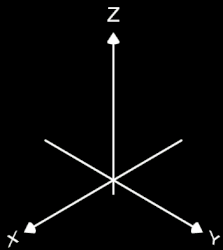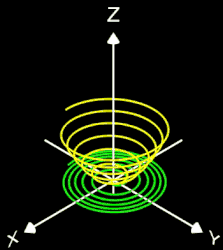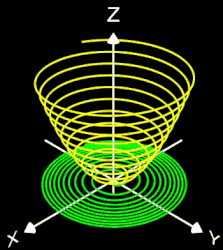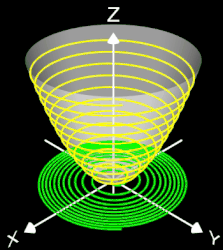
Auf dieser Seite liegt der Focus auf räumlichen Spiralen.
Für jeden Spiraltyp werden neben einigen Beispielen aus Natur und Technik dargestellt:
- Planare Spirale (Ausnahme Helix)
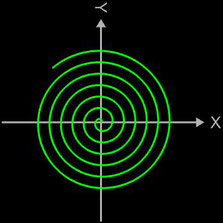
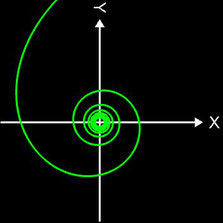
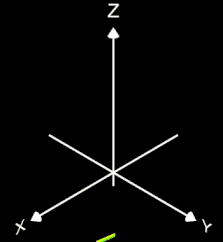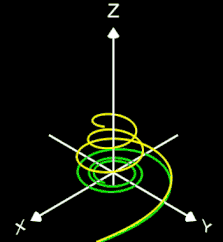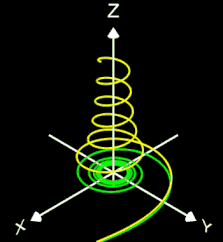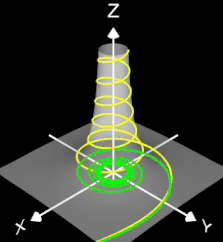
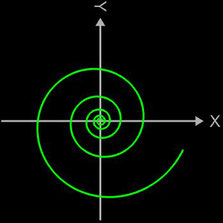
- 3D Spirale als Animation und Projektion der fertigen Spirale in die x/y-Ebene
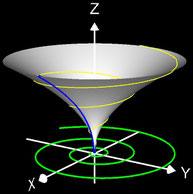
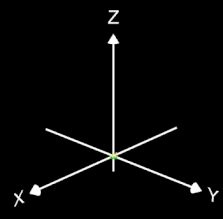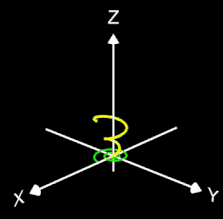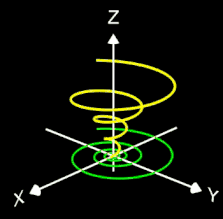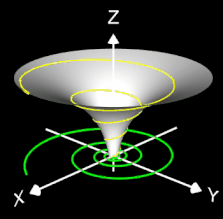
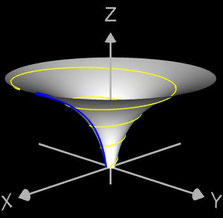
- korrespondierender Rotationskörper mit Randfunktion.
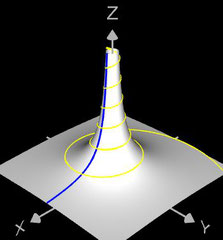
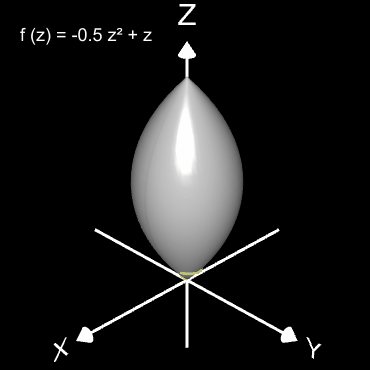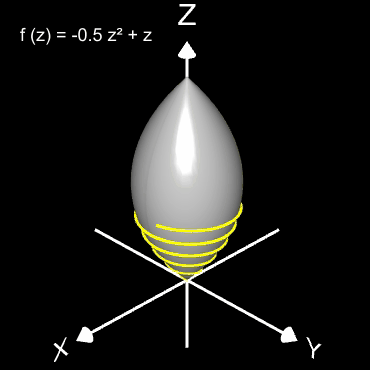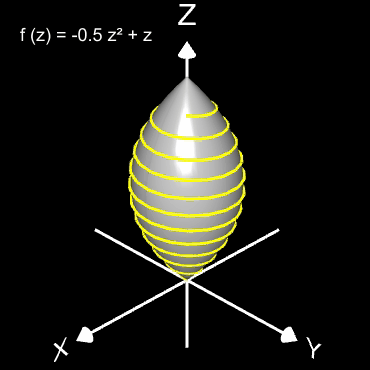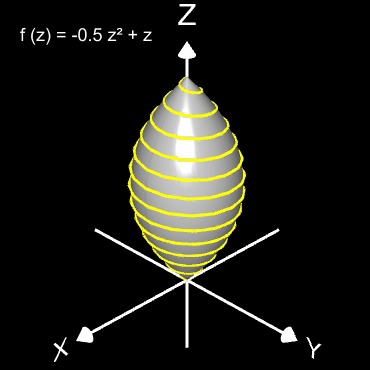
Für den Rotationskörper gilt
bzw.
wobei f (z) die den Rotationskörper erzeugende Randfunktion (blaue Linie in dne folgenden Diagrammen) mit ihrem Definitionsbereich Df ist.
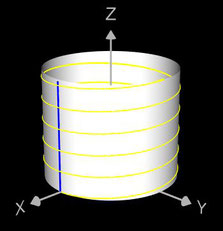
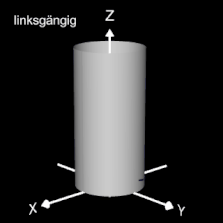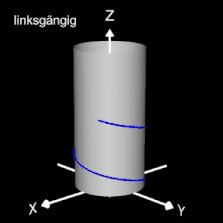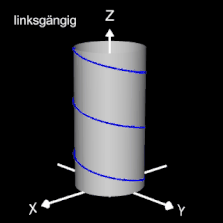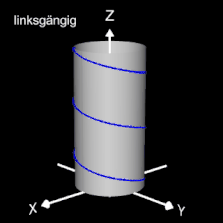
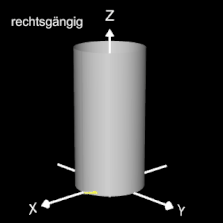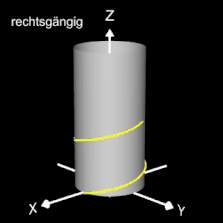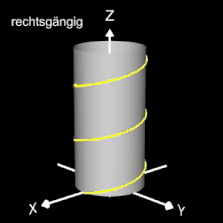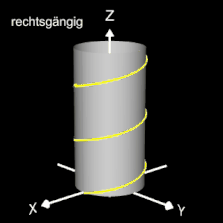
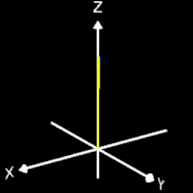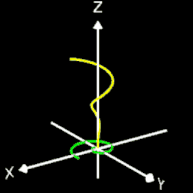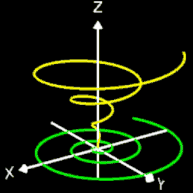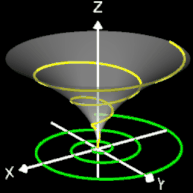
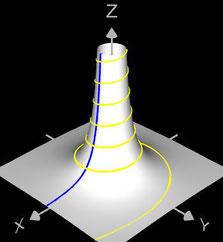
Helix (Schraubenlinie)
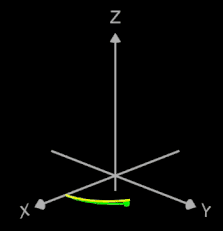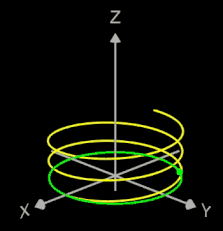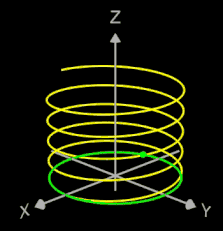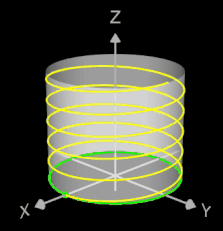
Die Helix ist eine Kurve, die sich mit konstanter Steigung um den Mantel eines Zylinders windet. Als Basis für die 3D-Herleitung dient hier nicht wie bei den folgenden 3D Spiralen eine planare Spirale, sondern ein Kreis, dessen Peripherie beliebig oft durchlaufen wird (grüner Punkt in der mittleren Grafik).
Kreis
Helix
Zylinder
Das Vorzeichen von c bestimmt die Drehrichtung (Gängigkeit) der Helix; dies gilt auch für die im folgenden betrachteten 3D Spiralen.
Die bisher betrachteten Helices befinden sich auf der Oberfläche von Zylindern. Am Ende der Seite finden Sie auch Helices auf beliebigen Rotationskörpern.
Konische Spirale
Die Basis für die konische Spirale ist die Archimedische Spirale. Bei dieser wächst entsprechend dem Proportionalitätsfaktor a der Radius ρ proportional mit dem Polarwinkel θ an, so dass der Abstand zwischen aufeinanderfolgenden Windungen konstant bleibt.
Archimedische Spirale
Konische Spirale
Kegel
Galileo-Spirale
Bei der Galileo-Spirale wächst der Radius ρ quadratisch mit dem Polarwinkel θ an. Sie ähnelt einer Logarithmischen Spirale, jedoch wächst bei letzterer der Radius exponentiell (s. u.).
Ein Beispiel aus der Natur ist der eingerollte Schwanz eines Chamäleons.
Quelle: www.terraristikshop.net
Galileo-Spirale
3D Galileo-Spirale
Rotationskörper zur
3D Galileo-Spirale
Paraboloide Spirale
Die Paraboloide Spirale entsteht aus der Fermat-Spirale. Bei dieser nimmt der Windungsabstand mit wachsender Entfernung zum Pol ab. Charakteristisch ist auch die stark gekrümmte erste Windung.
Fermat-Spirale
Paraboloide Spirale
Rotationsparaboloid
Hyperbolische Spirale
Bei der hyperbolischen Spirale hängen ρ und θ umgekehrt proportional zusammen. Dieser Zusammenhang - ähnlich wie bei Hyperbelfunktion in kartesischen Koordinaten - gibt der Spirale ihren Namen. Sie umrundet ihren Pol in unzähligen, immer enger werdenden Windungen, erreicht ihn jedoch nie.
Hyperbolische Spirale
3D Hyperbolische Spirale
Rotationshyperboloid
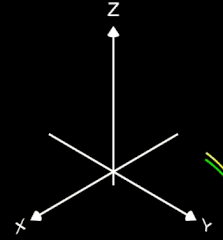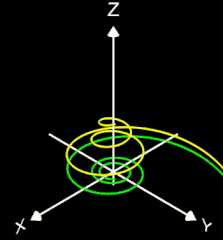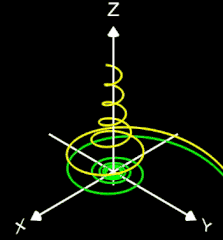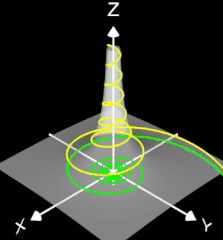
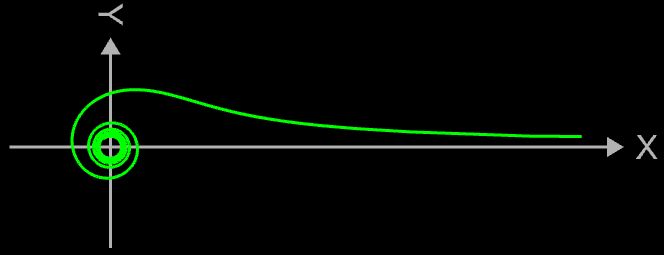
3D Lituus-Spirale
Die Lituus-Spirale verdankt ihren Namen der Ähnlichkeit mit einem Bischofsstab (s. Grafik rechts). Bei der Lituus-Spirale ist der Winkel θ umgekehrt proportional zum Quadrat des Radius ρ. Auch sie umrundet ihren Pol, ohne ihn jemals zu erreichen, während ihr äußerer Ast sich asymptotisch der x-Achse nähert.
Lituus-Spirale
3D Lituus-Spirale
Rotationskörper zur 3D Lituus-Spiral
3D Logarithmische Spirale
Die logarithmische Spirale unterscheidet sich deutlich von den bisher aufgeführten Spiralen. Ihr Radius ρ wächst exponentiell mit dem Polarwinkel θ bzw. der Polarwinkel hängt logarithmisch vom Radius ab. Auch ihr Pol ist ein asymptotischer Punkt.
Weinbergschnecke
Quelle: wikipedia.de
Tiefdruck-System über Grönland
Quelle: visibleearth.nasa.gov
Spiral Galaxy NGC 1232
Quelle: (apod.nasa.gov)
Mit der 3D Logarithmischen Spirale können z.B. Schnecken oder Meeresschnecken modelliert werden.
Logarithmische Spirale
3D Logarithmische Spirale
Rotationskörper zur 3D Logarithmischen Spirale
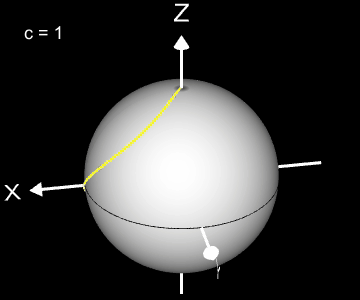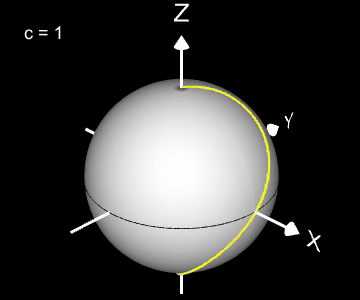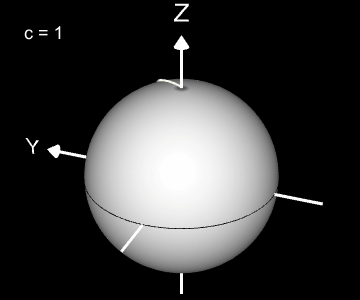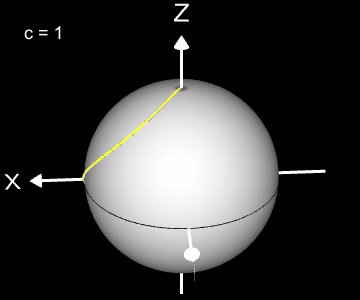
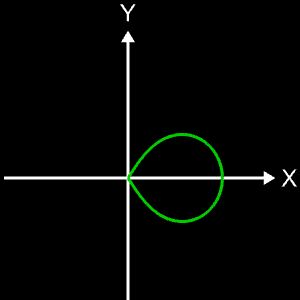
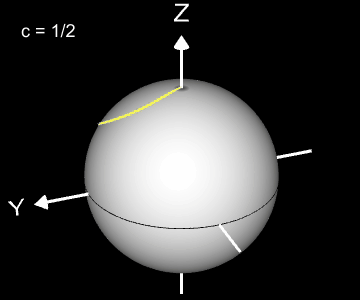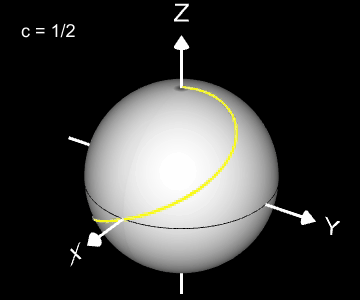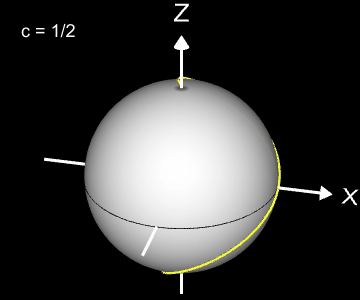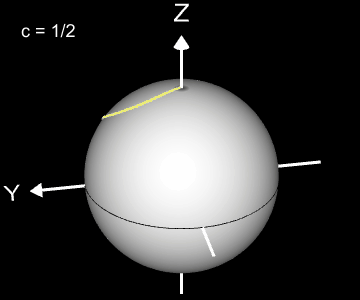
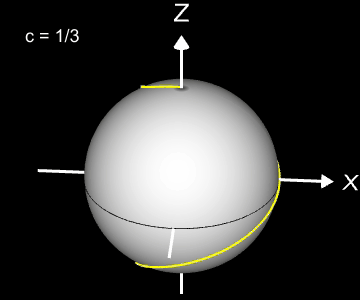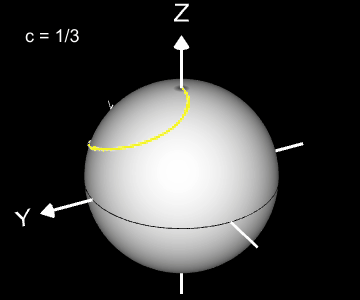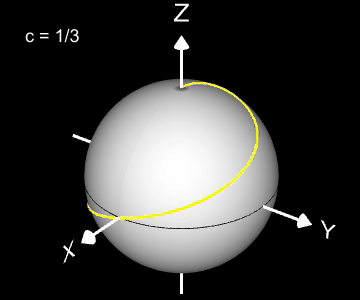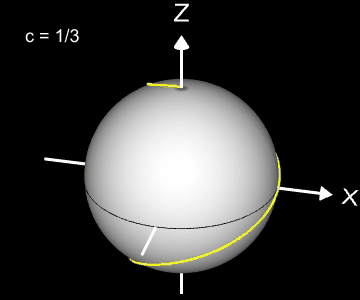
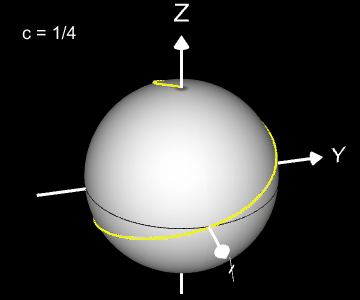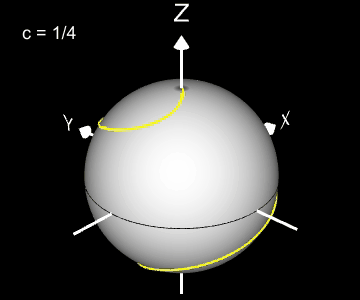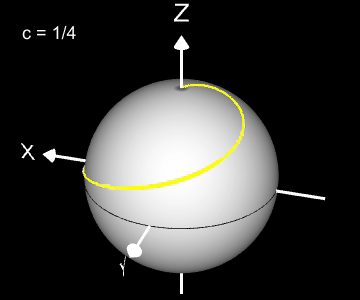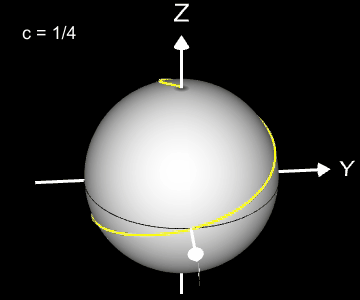
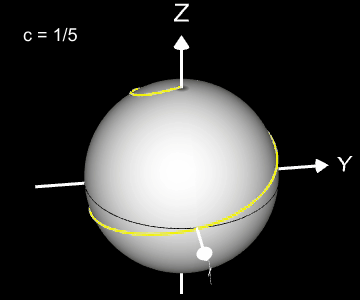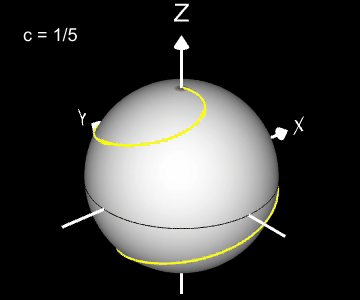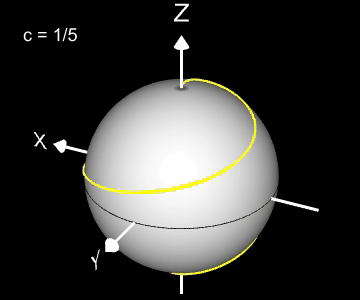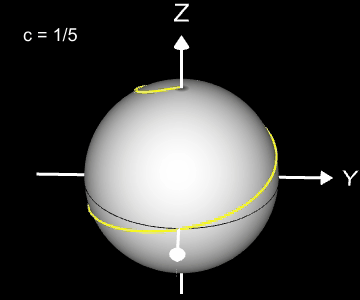
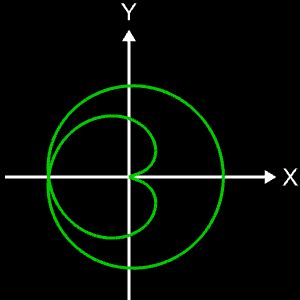
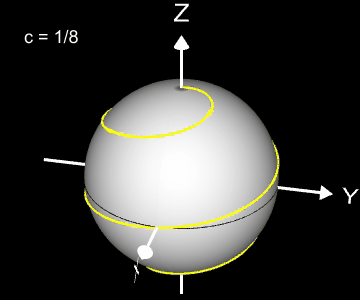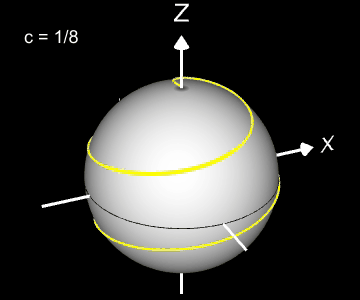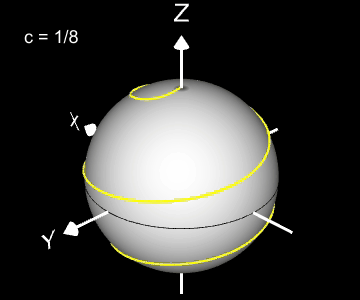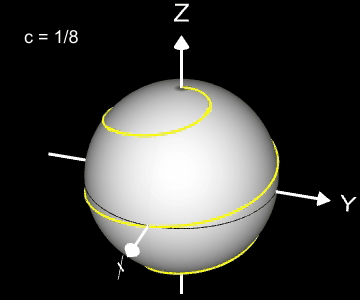
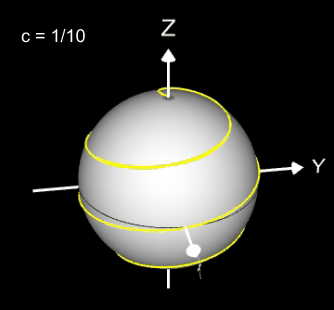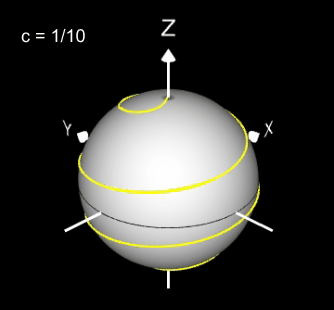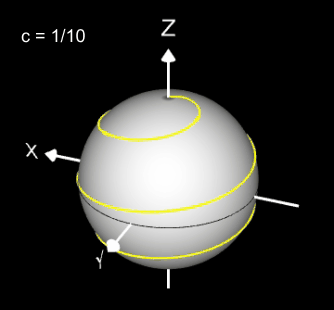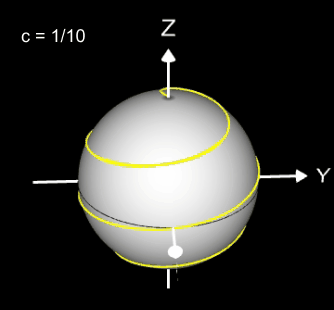
Kugelspirale
Eine weitere 3D Spirale ist die Kugelspirale. Diese windet entlang der Oberfläche einer Kugel, die sich z.B. aus der impliziten Gleichung x² + y² + z² = r² ergibt, wobei r der Radius der Kugel ist. Für die Kugelspirale gilt mit u ϵ [-r, r] :
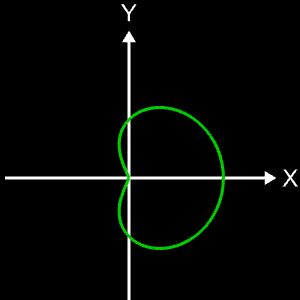
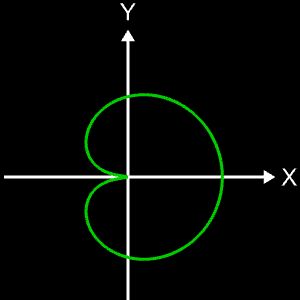
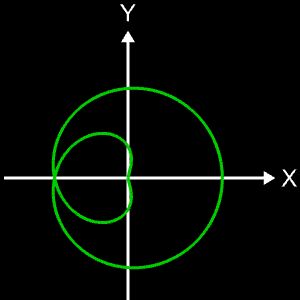
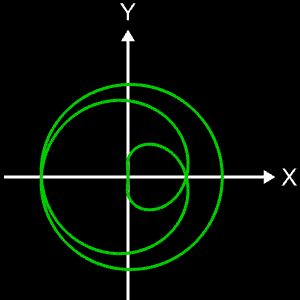
Die Projektion einr Kugelspirale in die x/y-Ebene erzeugt eine Clelia-Kurve [2]. In den folgenden Galerien sind für einige Werte von c die entstehende Kugelspiralen und die korrespondierende Cliela-Kurven dargestellt.
Die folgende Animation zeigt die entstehenden Clelia-Kurven, wenn c die Werte von 1 bis 0.05 durchläuft.
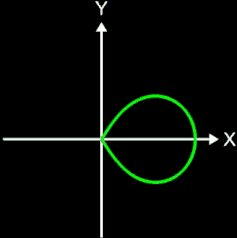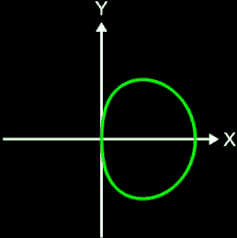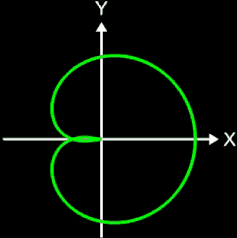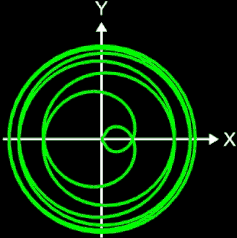
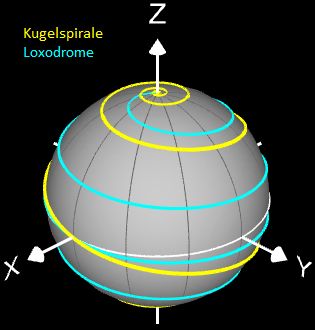
Abschließend sei noch angemerkt, dass man die Kugelspirale nicht mit der Loxodrome verwechseln darf. Diese letztere Spirale zeichnet sich dadurch aus, dass sie die Meridiane der Kugel stets im gleichen Winkel schneidet (s. auch Loxodrome). Zum Vergleich sind in den folgenden beiden Grafiken beide Spiralen dargestellt.
Helix auf beliebigen Rotationskörpern
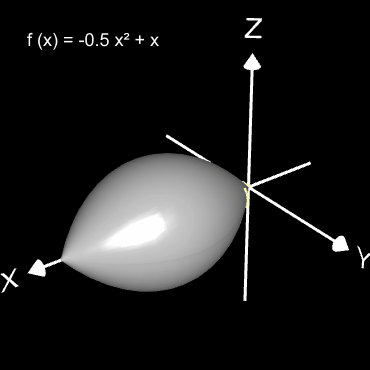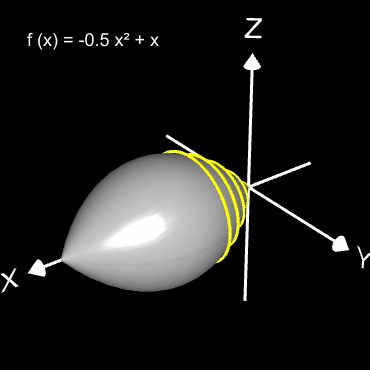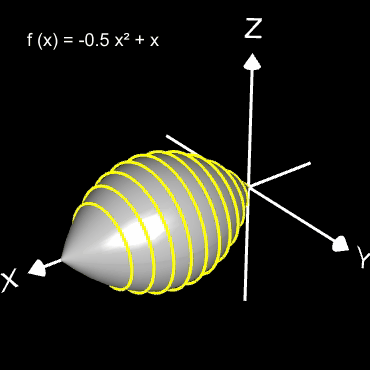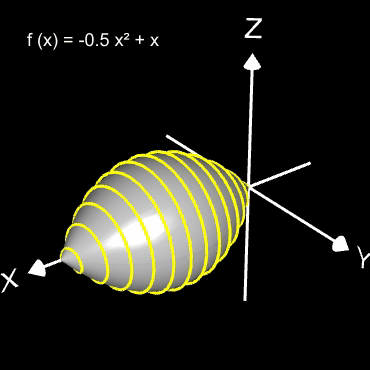
Ersetzt man den konstanten Radius r in der Parameterdarstellung der Helix durch die Randfunktion f eines Rotationskörpers, so erhält man einen spiralförmigen Verlauf auf der Oberfläche des Rotationskörpers:
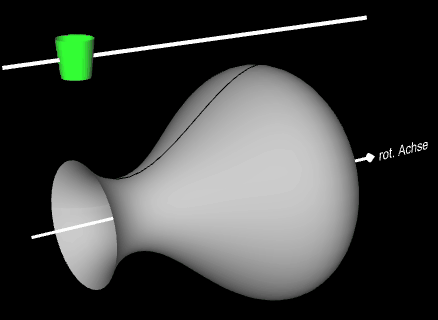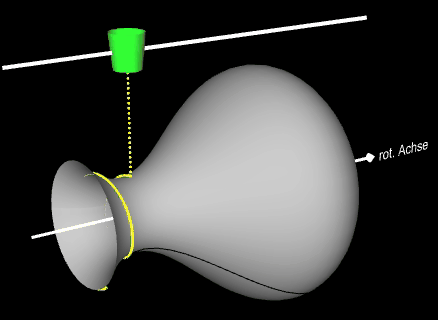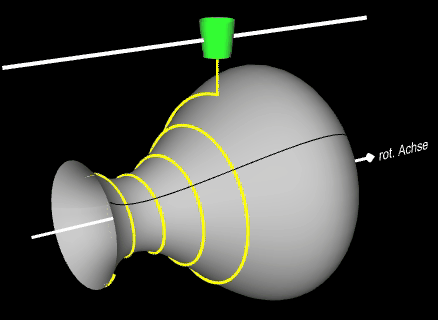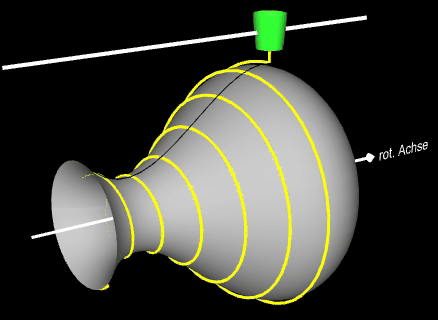
Im folgenden soll noch eine "Anwendung" einer Helix auf einem beliebigen Rotationskörper betrachtet werden.
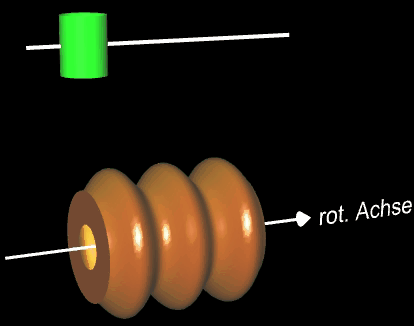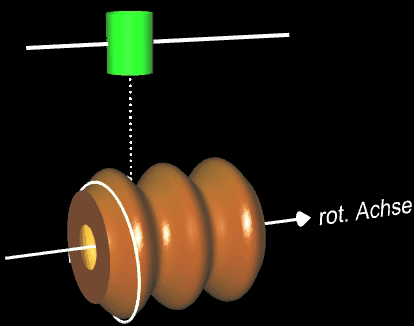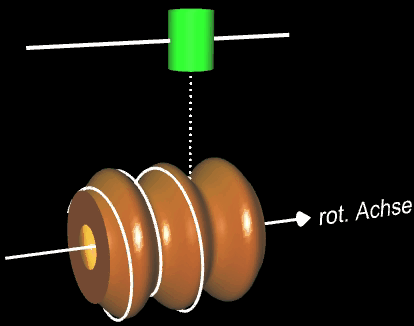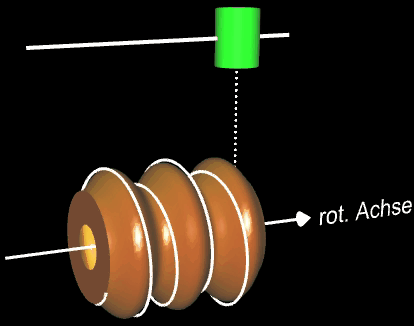
Auf eine Vase - Rotationskörper um die x-Achse mit der Randfunktion f (x) = -0.1 (2x³ -11x² +12x -9) mit x ϵ [0, 4] - soll eine farbige Helix längs der x-Achse aufgetragen werden. Während sich die Vase um die x-Achse dreht (um dies besser erkennen zu können, habe ich zwei dunkle"Längsnähte" auf der Vase angebracht), fährt oberhalb parallel zur x-Achse eine Farbspritzdüse (grün) entlang. Hierzu müssen die Translation der Düse und die Rotation der Vase so synchronisiert werden, dass sich das Ende der Helix stets oben und unterhalb der Düse befindet:
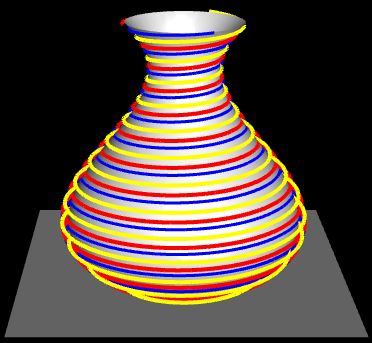
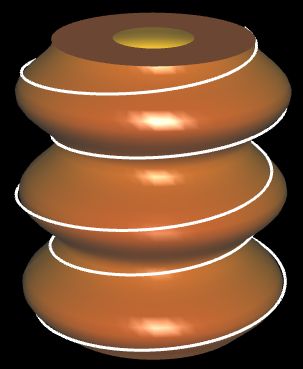
Das rechte Bild in der obigen Galerie zeigt eine "Ziervase" mit versetzt angeordneten farbigen Spirallinien.
Das gleiche Prinzip nutzend und mit der Randfunktion f (x) = 0.2 sin ² (6x) + 0.5 mit x ϵ [0, 1.5] entsteht ein "Baumkuchen", auf den eine Helix aus "Zuckerguss" aufgetragen wird:
Quellenverweise
[1] J. Heitzer (2002) Mathe-Welt "Spiralen", mathematik lehren, 111, S. 23-46