3D Zahnrad
Kaum etwas symbolisiert die menschliche Technik so sehr wie das Zahnrad. Das Prinzip der Kraftübertragung durch verzahnte Räder nutzt der Mensch schon seit der Antike.
Konstruktion eines 3D Zahnrads
Zunächst muss eine "Zahnradkurve" konstruiert werden.
Ausgangspunkt hierfür ist ein Kreis mit dem Radius a und der Parameterdarstellung
x (u) = a cos (u)
y (u) = a sin (u) mit u = 0 ... 2 π.
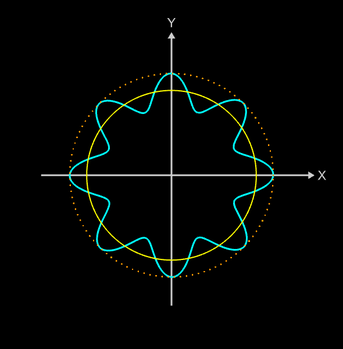
Auf den festen Radius a werden nun n "Zähne" mit der Amplitude b aufmoduliert, was zu folgender Radius-Funktion führt
r (u) = a + b sin (n • u) mit n = 0, 1, 2, 3, ...
Die entstehende Kurve hat mit einem Zahnrad noch wenig zu tun: der obere Teil der "Zähne" muss flacher verlaufen, die Flanken hingegen steiler.
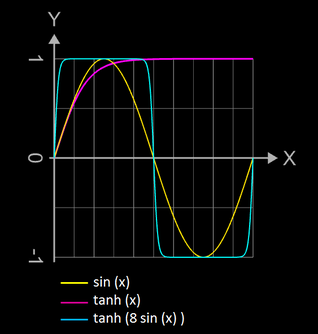
Dies kann recht einfach mit Hilfe der Funktion tanh und einem Faktor c >> 1 umgesetzt werden, wie das folgende Diagramm zeigt:
Angewandt auf das bisherige Modell ergibt sich
r (u) = a + tanh [ c • b sin (n • u) ]
x (u) = r (u) cos (u)
y (u) = r (u) sin (u) mit u = 0 ... 2 π (s. linkes Bild unten)
Die Amplitude der neuen Zähne muss noch mit einem Faktor d << 1 angepasst werden
r (u) = a + tanh [ c • b sin (n • u) ] • d
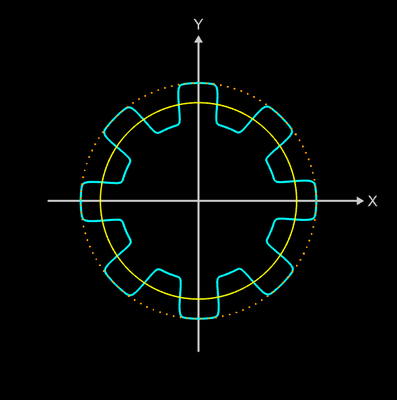
und ... fertig ist die Zahnradkurve (s. rechtes Bild):
Durch einen Vergleich der Parameter b, c und d erkennt man, dass sich die Zahnradkurve noch weiter vereinfachen lässt:
r (u) = a + tanh [ b • sin (n • u) ] • b
x (u) = r (u) cos (u)
y (u) = r (u) sin (u) mit u = 0 ... 2pi.
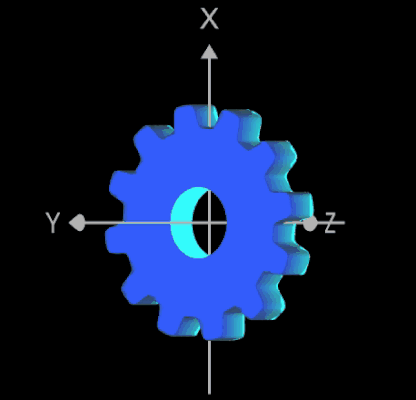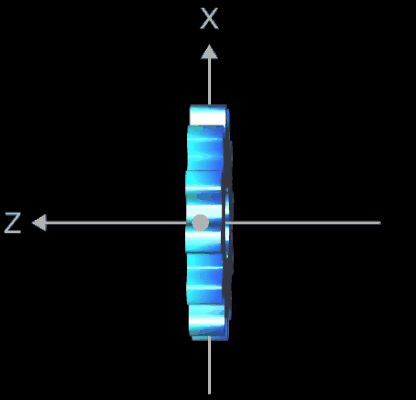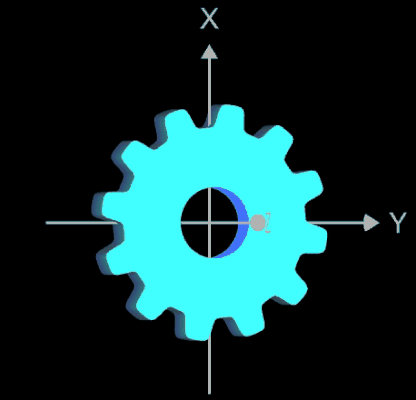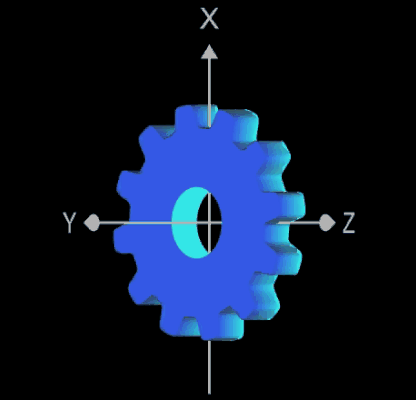
Das 3D-Modell des Zahnrads besteht aus den Komponenten
- planare Lochscheibe mit Zähnen
- senkrecht dazu stehenden Zahnflanken mit einer Höhe D
- zylindrische Bohrung mit dem Radius rB
die alle mit parametrischen Funktionen realisiert werden (v = 0, ..., 1):

Addiert man zum Parameter u noch einen weiteren Parameter t und animiert diesen, so dreht sich das Zahnrad (für die ntgegengesetzte Drehrichtung wird t subtrahiert).
Falls Sie als Besucher dieser Seite von Beruf Maschinenbauer / technischer Konstrukteur sind, mögen Sie mir bitte diese einfache Konstruktion verzeihen - ich weiß, dass die Konstruktion von Zahnrädern recht aufwendig ist und viele Parameter berücksichtigt werden müssen ...
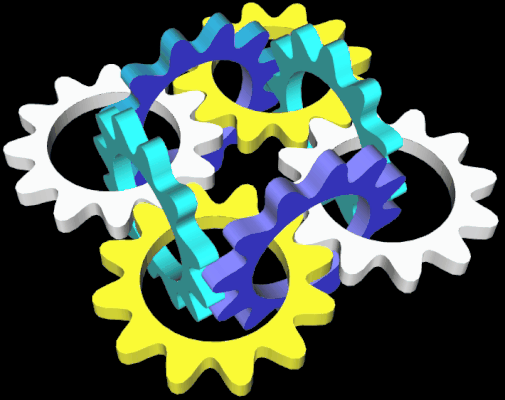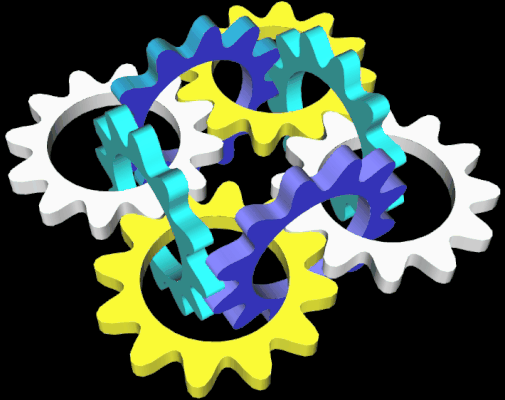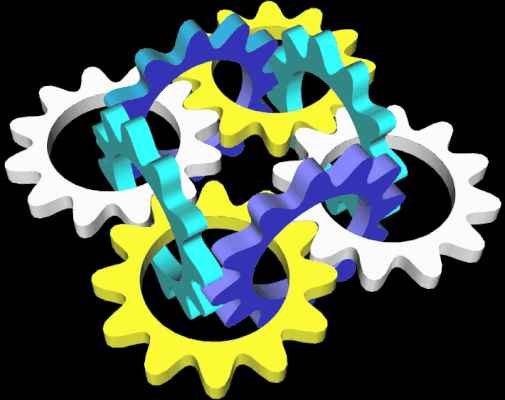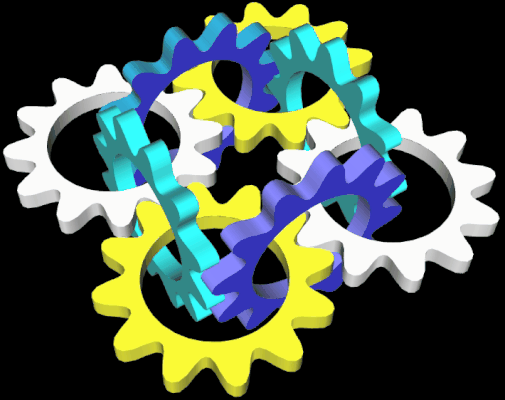
In der folgenden Galerie finden Sie ein paar Konstellationen mit meinem Zahnradmodell, die ich mit Graphing Calculator 3D erzeugt habe (die Ruckler entstehen bei der Erzeugung des animierten GIF-Bildes; ich wollte die Dateigröße nicht allzu groß werden lassen):
Nachfolgend sind noch Anordnungen aus Zahnrädern dargestellt, bei denen die Zahnradoberflächen nicht in einer gemeinsamen Ebene liegen.
Weitere Zahnradkonstellationen finden Sie bei 3D Nockenwelle und 3D Riementrieb.
Alternatives Zahnradmodell
Um ein Zahnrad mit der obigen Methode zu modellieren, benötigt man außer der Zahnradkurve r drei parametrische Funktionen für die Zahnradteile obere / untere Fläche und Zahnflanken sowie eine weitere parametrische Funktion (Zylinder) für die Bohrung. Für die Modellierung komplexerer Anordnungen, wie z.B. beim Planetengetriebe (s. Galerie unten) ergibt sich somit schon ein größerer Editieraufwand.
Mit Hilfe der Funktionen
erzeugt eine einzige parametrische Funktion
x = [1-min(int(|u|),1)] • (rB+r(v))•cos(v+t)+min(int(|u|),1) • [rB+r(v)-(|u|-1) • r(v)] • cos(v+t)
y = [1-min(int(|u|),1)] • (rB+r(v))•sin(v+t)+min(int(|u|),1) • [rB+r(v)-(|u|-1) • r(v)] • sin(v+t)
z = 0.5 • range(-1,1,u)
mit u = -2, ..., 2 und v = 0, ..., 2π das bis auf die Wand der Bohrung vollständige Zahnrad "in einem Guss":
Abschließend noch ein animiertes "künstlerisches" Objekt - ich nenne es "Verzahnt" ... :-)