3D Pyramide
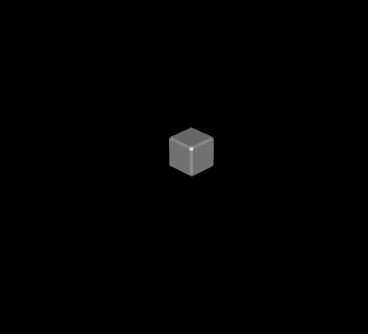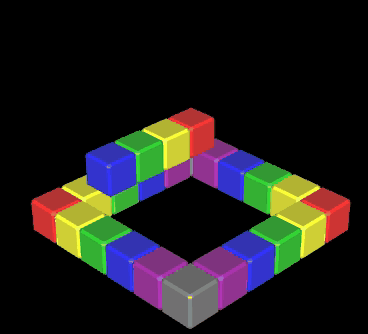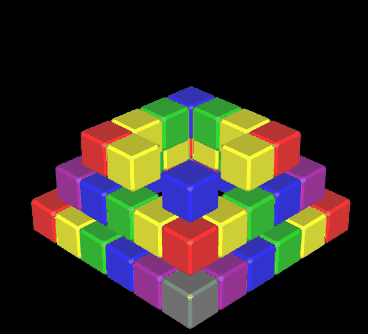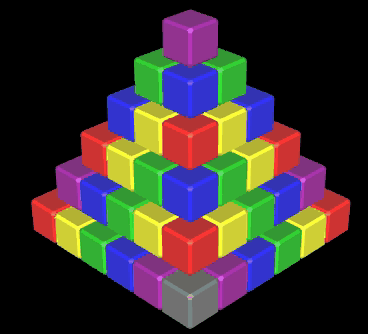
... eine kleine Spielerei aus der Zeit meiner ersten Schritte mit Graphing Calculator 3D, die eindrucksvoll die Leistungsfähigkeit des Programms zeigt (s.u.).
Mit einer Variable level kann die Höhe der Pyramide zwischen 0 (löschen) und 6 eingestellt werden. Auf Grund der Bauweise - jede Ebene besteht aus einem "Ring" von Würfeln (s. obige Animation) - ergibt sich die Anzahl w (k) benötigter Würfel für eine Pyramide der Höhe k ∈ |N gemäß
w (k) = 2 k² - 2 k + 1 = k² + (k-1)²
Für k ∈ |N ergibt sich die Folge der zentrierten Quadratzahlen 1, 5, 13, 25, 41, .... (Folge A001844 in OEIS) [1]. Für k = level = 6 werden somit 61 Würfel erzeugt.
Pro Würfel mit der Kantenlänge 2 und seinem Mittelpunkt (xc, yc, zc) ist eine Funktion definiert (s. auch Modellierung 3D Würfel):
f i (x, y, z, xc, yc, zc) = max (max (| x - 2 xc |, | y – 2 yc |), | z – 2 zc | ) -1
mit level ≥ L i = 1, ... 61
Dabei bestimmt L ϵ {1, …, 6} ab welcher Höhe der Würfel sichtbar sein soll.
Geplottet werden die Würfel mittels 61 impliziter Funktionen der Form
f i (x, y, z, ..., ..., ...) = 0
mit den jeweiligen Mittelpunktskoordinaten und der Farbe des Würfels.
Zeitaufwand
Pro Würfel zwei implizite Funktionen (Abfrage auf Sichtbarkeit anhand von level und Darstellung)
Eingabe der Funktionenliste: ~ 3 h :-(
Rechenzeit für 61 Würfel mit Auflösung 2: < 2 sec. :-))
Dabei werden pro Würfel 1177 Datenpunkte erzeugt.
Bei einer Auflösung von 3 werden pro Würfel 2905 Datenpunkte berechnet, die Rechenzeit für 61 Würfel liegt dann bei ~ 12 Sekunden.
Alternative Darstellung
Würde man einen Würfel als Super-Ellipsoid in Parameterdarstellung (s. Modellierung 3D Würfel) erzeugen, hätte man schon bei einer Auflösung von 2 scharfe Kanten, und die Rechenzeit würde sich somit deutlich reduzieren. Allerdings kämen auf Grund der parametrischen Darstellung noch einmal 2 Terme (Zeilen in der Funktionenliste) pro Würfel hinzu, d.h. zu den 122 Zeilen mit impliziten Funktionen kämen noch einmal 122 Zeilen hinzu - dies wollte ich mir aber nicht antun ... ;-)
Lediglich die beiden oberen Ebenen der Pyramide habe ich einmal als Super-Ellipsoide in Parameter-darstellung erzeugt:
Die Kanten sind sehr exakt, das Ganze wirkt aber sehr unnatürlich, und man sieht, dass es sich um eine Computergrafik handelt.
Nett anzuschauen und ohne großen Aufwand durch Ersetzen der obigen Funktion mit
f i (x, y, z, xc, yc, zc) = (x - 2 xc)4 + (y - 2 yc)4 + (z - 2 zc)4 - 1 ;level ≥ L
und gleicher Auflösung entstehenden recht "knuffige", fast echt wirkende Würfel:
Kugelpyramide und quadratische Pyramidalzahl
Eine ähnliche Anordnung wie oben von Objekten zu einer Pyramide sind Kugelpyramiden und die damit zusammenhängenden quadratischen Pyramidalzahlen [2]. Diese beziffern die Anzahl von Kugeln, mit denen man eine Pyramide quadratischer Grundfläche bauen kann.

Wie man in der folgenden Animation am Beispiel einer Pyramide der Höhe n = 4 erkennt, ergibt sich die vierte quadratische Pyramidalzahl P (4) = 30 als Summe der ersten vier Quadratzahlen.

Allgemein gilt:
Dies ergibt die quadratischen Pyramidalzahlen 1, 5, 14, 30, 55, 91, … (Folge A000330 in OEIS).
Diese Formel wurde bereits Ende des 16. Jahrhunderts hergeleitet, als es um das Zählen von Kanonenkugeln ging, die in einer quadratischen Pyramide angeordnet ("gestapelt") sind. Für interessierte Leser und um nicht aus der Übung zu kommen, finden Sie für die obige Summenformel der Pyramidalzahlen einen Beweis mittels Vollständiger Induktion. Klicken Sie hierfür bitte auf das Minibild in der rechten Spalte.

Im Zusammenhang mit quadratischen Pyramidalzahlen taucht auch das Kanonenkugel-Problem (engl. cannonball problem) auf [3], bei dem die Frage gestellt wird, welche Zahlen sowohl quadratisch als auch quadratisch-pyramidal sind.
Das Problem kann auch folgendermaßen formuliert werden: Gegeben sei eine quadratische Anordnung von m² Kanonenkugeln; bei welcher Quadratgröße können diese Kanonenkugeln auch in einer quadratischen Pyramide (s. Bild [4] rechts) angeordnet werden?
Gesucht sind somit Paare (n, m) als Lösung der diophantischen Gleichung
Schnell findet man die Lösungspaare (0, 0), (1, 1) und (24, 70):
Im Fall (24, 70) entspräche dies 4900 Kanonenkugeln.
Im Jahr 1875 postulierte der französische Mathematiker Édouard Lucas (1842 - 1891), dass die zuvor genannten drei Paare die einzig möglichen seien. Erst 1918 wurde der entsprechende Beweis hierfür erbracht [3].


