Kugelpyramide und quadratische Pyramidalzahl
Bei einer Kugelpyramide sind Kugeln gleichen Durchmessers zu einer Pyramide aufgestapelt:
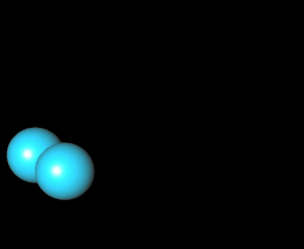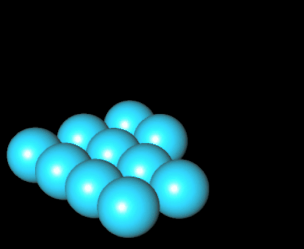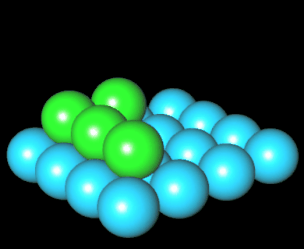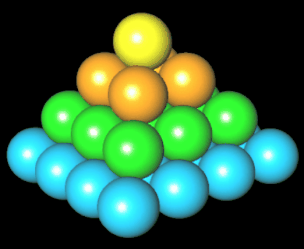
Die Anzahl von Kugeln, mit denen man eine Pyramide quadratischer Grundfläche bauen kann, geben die
quadratischen Pyramidalzahlen [1] an. Wie man in der folgenden Animation am Beispiel einer Pyramide der Höhe n = 4 erkennt, ergibt sich die vierte quadratische Pyramidalzahl P (4) = 30 als Summe der ersten vier Quadratzahlen.
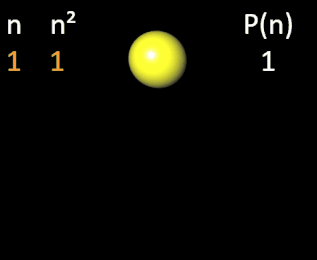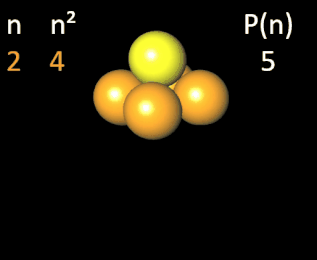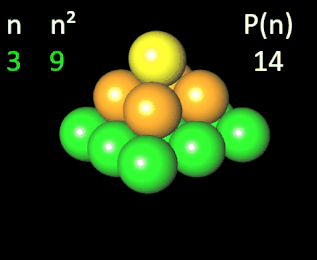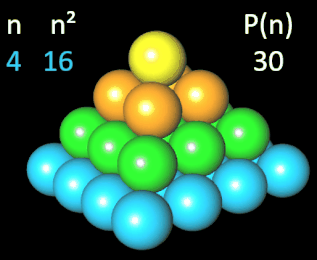
Allgemein gilt:
Dies ergibt die quadratischen Pyramidalzahlen 1, 5, 14, 30, 55, 91, … (Folge A000330 in OEIS).
Diese Formel wurde bereits Ende des 16. Jahrhunderts hergeleitet, als es um das Zählen von Kanonenkugeln ging, die in einer quadratischen Pyramide angeordnet ("gestapelt") sind. Für interessierte Leser und um nicht aus der Übung zu kommen, finden Sie für die obige Summenformel der Pyramidalzahlen einen Beweis mittels Vollständiger Induktion. Klicken Sie hierfür bitte auf das Minibild in der rechten Spalte.

Im Zusammenhang mit quadratischen Pyramidalzahlen taucht auch das Kanonenkugel-Problem (engl. cannonball problem) auf [2], bei dem die Frage gestellt wird, welche Zahlen sowohl quadratisch als auch quadratisch-pyramidal sind.
Das Problem kann auch folgendermaßen formuliert werden: Gegeben sei eine quadratische Anordnung von m² Kanonenkugeln; bei welcher Quadratgröße können diese Kanonenkugeln auch in einer quadratischen Pyramide (s. Bild [3] rechts) angeordnet werden?
Gesucht sind somit Paare (n, m) als Lösung der diophantischen Gleichung
Schnell findet man die Lösungspaare (0, 0), (1, 1) und (24, 70):
Im Fall (24, 70) entspräche dies 4900 Kanonenkugeln.
Im Jahr 1875 postulierte der französische Mathematiker Édouard Lucas (1842 - 1891), dass die zuvor genannten drei Paare die einzig möglichen seien. Erst 1918 wurde mittels eliptischer Funktionen der entsprechende Beweis hierfür erbracht [2], in neuerer Zeit auch als elementarer Beweis [4].
Quellenverweise
[1] https://de.wikipedia.org/wiki/Quadratische_Pyramidalzahl
[2] https://en.wikipedia.org/wiki/Cannonball_problem
[3] https://commons.wikimedia.org/wiki/File:Rye_Castle,_Rye,_East_Sussex,_England-6April2011_(1).jpg
[4] Q. Huan, P. Yuan (2019) An elementary proof of a result Ma and Chen,
arXiv:1903.00121v1 [math.NT] 1 Mar 2019

