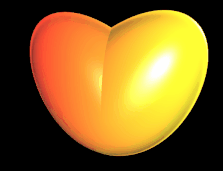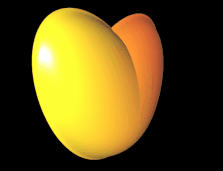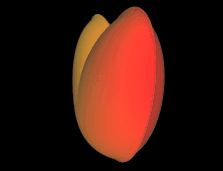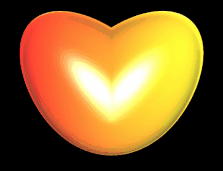3D Herz
Im Unterricht hatten wir schon einige Objekte als Rotationskörper konstruierrt, als die Schülerinnen mich fragten, ob man denn auch ein 3D-Herz erzeugen könne. Schnell konnten wir klären, dass zum einen das gewünschte 3D-Herz kein Rotationskörper ist und zum anderen die bis dato behandelten Funktionstypen nicht ausreichen, um die "Kerbe" im Herz zu erzeugen.
Zumindest fand ich nach kurzer Internet-Recherche eine geeignete Formel in impliziter Form [1]
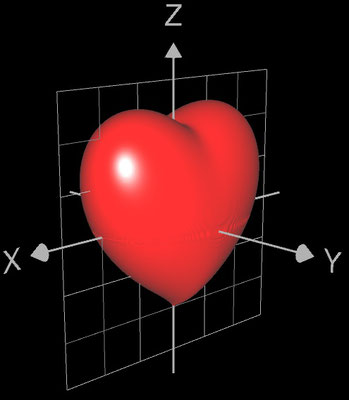
(x² + 9/4 y² + z² - 1) ³ - x² z³ - 9/80 y² z³ = 0 ♥
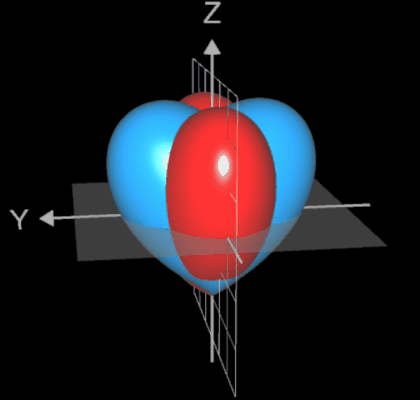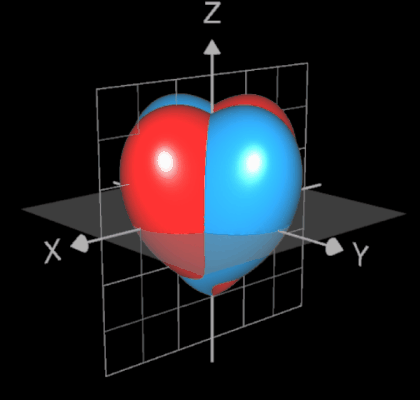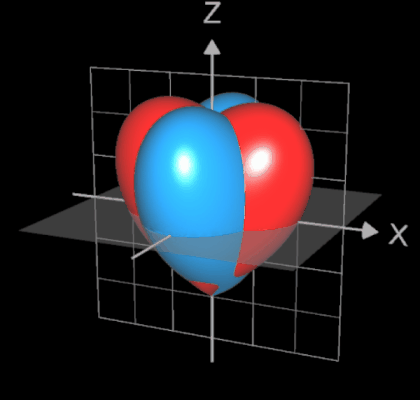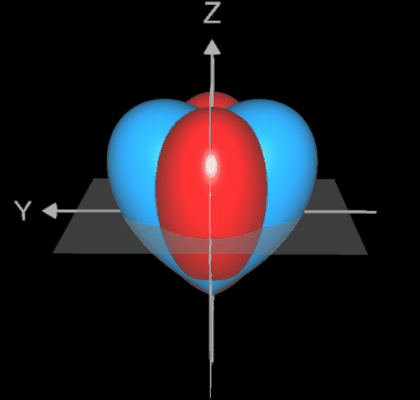
und konnte das Herz mit GC3D darstellen (s.o.). Es handelt sich dabei um eine Algebraische Kurve [2] vom Grad 6.
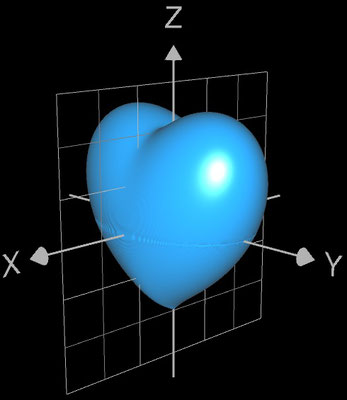
Bei späteren Recherchen fand ich eine etwas andere implizite Darstellung deutlich älteren Datums [3]:
(2 x² + y² + z² - 1) ³ - 1/10 x² z³ - y² z³ = 0 ♥
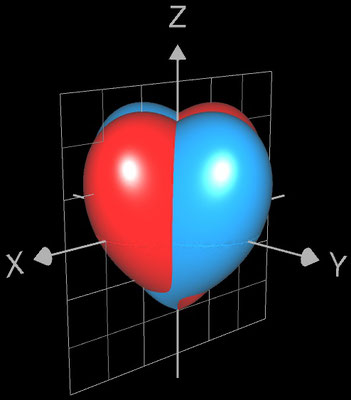
Interessant ist die Position des entstehenden Herzens (♥) im Koordinatensystem: es ist gegenüber dem vorigen Herz (♥) um 90° gedreht.
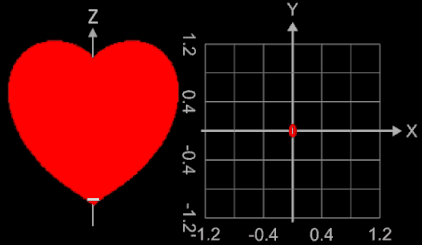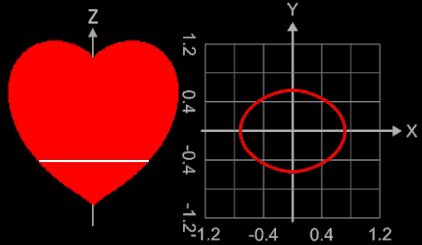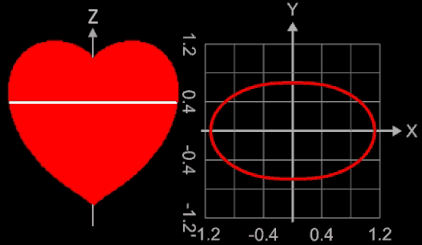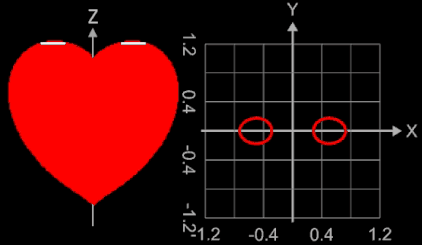
Betrachtet man die Konturlinien (Ränder der Querschnittsflächen senkrecht zur z-Achse) ausgehend von der Herzspitze bei z = -1 nach oben, so sind diese zunächst ellipsenförmig mit Hauptachse in y-Richtung, ändern sich dann in ellipsensähnliche Formen mit Hauptachse in x-Richtung. Bei z = 0 liegt eine echte Ellipse vor, dann entstehen Formen ähnlich einer Cassini-Kurve.
Etwas unbefriedigend bei beiden Herzen ist die wellige Oberfläche. Dies ist ein Problem des Graphing Calculator 3D, das oftmals bei Impliziten Funktionen auftaucht. Wählt man eine hohe Auflösung, so verbessert sich zwar die Darstellung, jedoch führt dies zum eine zu sehr langen Rechenzeiten und man erreicht zum anderen irgendwann die maximale Speichergröße von Graphing Calculator 3D.
Welche weiteren Möglichkeiten gibt es, ein 3D Herz mathematisch zu modellieren?
Eine erste Idee ist es, eine zweidimensionale Kardioide ("Herzkurve") mit einem Halbkreis als Sphärisches Produkt darzustellen und die "Dicke" mit einem Faktor anzupassen (für eine Erklärung hierzu und ein Beispiel mit einer Kardioide siehe unter Spezielle 3D Flächen/Supershape).
Das Herz rechts basiert auf der Funktion
h1 (ω) = | ω | cos (ω)
h2 (ω) = | ω | sin (ω) mit - π ≤ ω ≤ π
Die weiteren 3D Herzen wurden alle als Supershape erzeugt, wobei sowohl die horizontale als auch die vertikal modulierende Funktion mit Hilfe einer
Superformel SF ( a, b, m1, m2, n1, n2, n3 ) umgesetzt sind.
Zum eigenen Experimentieren kann auch die in Spezielle 3D Flächen/Supershape
angegebene Graphing Calculator 3D-Datei Supershape.gc3 verwendet werden.
SFh (1, 4, -2.6, -2.6, 2.5, 2,
1.5)
SFm
( 1, 1, 1, 1, 2, 2, 2)
SFh (1, 4, -2.6, -2.6, 2.5, 2, 1.5)
SFm ( 1, 1, 2, 2, 1, 1, 1 )
SFh (1, 4, -2.6, -2.6, 2.5, 2, 1.5)
SFm ( 1, 20, 1, 1, 1, 0.4, 0.4 )
SFh (1, 2, -2.6, -2.6, 1, 2,
1.1)
SFm (1, 1, 1, 1, 2, 2, 2)
SFh (1, 4, -2.6, -2.6, 2.5, 2,
1.5)
SFm
( 0.5, 0.5, 1, 1, 2, 2, 2 )
SFh (1, 2, -2.6, -2.6, 1, 2,
1.1)
SFm
( 0.5, 0.5, 1, 1, 2, 2, 2 )
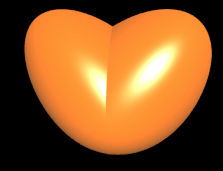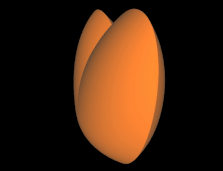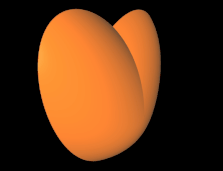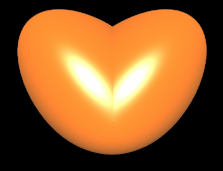
Die beiden letzten Herzen (gelb und blau) wurden als Supershape auf einem Torus generiert, wie es in
Spezielle 3D Flächen/Supershape erläutert wird.
Beim folgenden "Lollipop-Herz" wurde dieses in gelb und rot nacheinander geplottet, wobei die roten Streifen dadurch entstehen, dass auf die z-Komponente des roten Herzen der Term 0.02 sin (20u) addiert wurde.
Eine weitere Möglichkeit ein 3D Herz zu erzeugen besteht darin, eine "Herzkurve" in parametrischer Form als Rohr/Röhre darzustellen (s. dazu Funktionsgraph als Rohr/Röhre). Die folgende Galerie zeigt die entstehenden Herzen für die Funktionen
- blaues Herz [4], u = 0 ... 60
- rotes Herz [5], u = 0 ... 2π
Bei den letzten beiden roten Herzen wurde für die Ummantelung der Herzkurve ein elliptischer Querschnitt verwendet.
Weitere Herzkurven, mit denen sich u. a. die obigen Ummantelugen erzeugen lassen, finden sie im Bereich 2D Mathe auf der Unterseite Herzkurven.
Abschließend noch ein "wellenförmiges Herz", das sich als Plot einer Funktion mit zwei Variablen ergibt gemäß:
Quellenverweise
[1] https://tpenguinltg.wordpress.com/2014/02/15/representing-the-heart-shape-precisely/
[2] https://de.wikipedia.org/wiki/Algebraische_Kurve
[3] G. Taubin (1993) An Accurate Algorithm for
Rasterizing Algebraic Curves,
Second ACM /IEEE
Symposium on Solid Modeling and Applications Proceedings,May 1993, 221-230