3D Fliehkraftregler
In einer gemeinsamen Firma produzierte James Watt (1736 - 1819) zusammen mit Matthew Boulton (1728 - 1809) Dampfmaschinen. Ein Problem bestand darin, dass zum Erreichen einer konstanten Drehzahl die Dampfzufuhr laufend manuell eingestellt werden musste. Im Jahr 1788 entdeckte Boulton den Fliehkraftregler beim Windmühlenbau und setzte ihn zur Drehzahlregelung der Dampfmaschinen ein [1].
Watt / Boulton-Regler
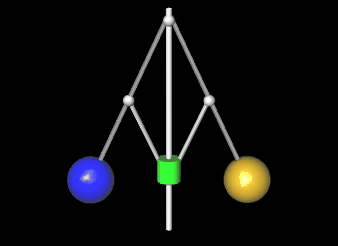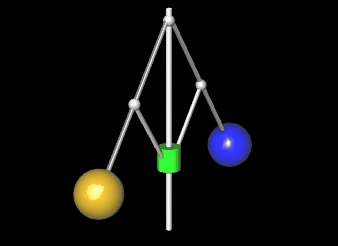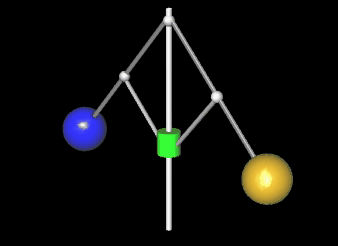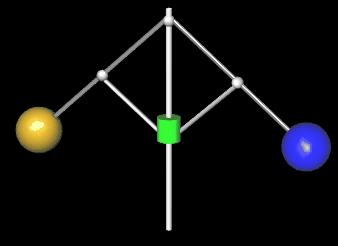
An einer mit der Winkelgeschwindigkeit ω rotierenden Drehachse sind zwei Hebel der Länge L beweglich befestigt, an deren Enden sich zwei Kugeln der Masse M befinden [2]. Im Abstand a vom Drehpunkt sind an den Hebeln zwei weitere kurze Stangen der Länge a befestigt, die eine auf der Achse gleitende Hülse der Masse m heben oder senken. Je größer die Winkelgeschwindigkeit ist, desto größer wird der Winkel α zwischen Achse und Hebel und desto höher steigt die Hülse.
![Watt / Boulton Fliehkraftregler [2]](https://image.jimcdn.com/app/cms/image/transf/none/path/scee86bccd27a6ab2/image/i227557b3d3ddbd0d/version/1582972986/image.png)
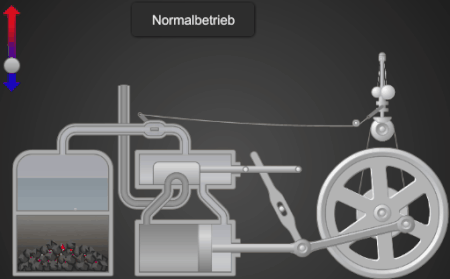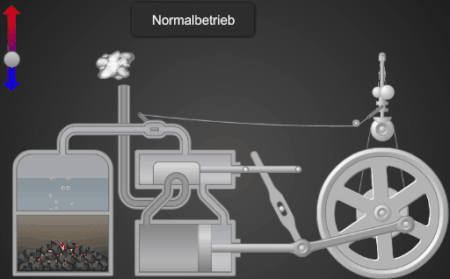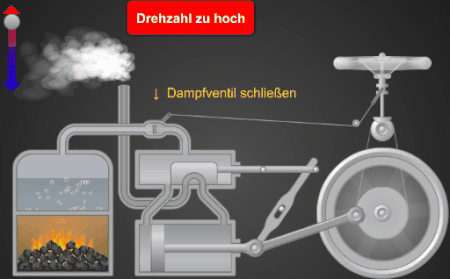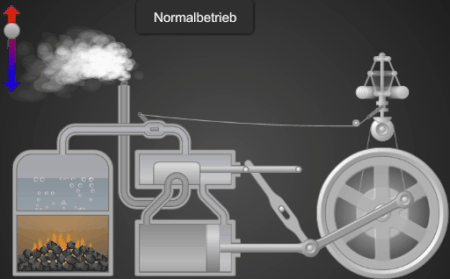
Diese Höhenänderung wird über ein Hebelsystem zur Regelung der Dampfzufuhr bei der Dampfmaschine genutzt, s. folgende Animation [3].
Für die obige Animation des Fliehkraftreglers wird der Winkel α zwischen Mittel- und Gewichtsstange benötigt. Aus diesem können dann weitere Größen, wie z.B. die Höhe h des Gleitzylinders und die räumliche Position der Mittelpunkte der Gewichtskugeln hergeleitet werden.
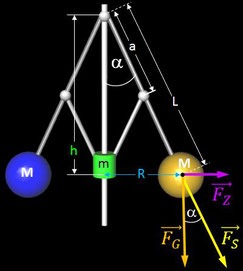
Im Gleichgewichtsfall ist - unter Vernachlässigung des Gewichts der Hülse mit der Masse m und der Stangen - die vektorielle Summe der Gewichtskraft F⃗G der Kugelmasse M und der an der Stange ziehenden Kraft F⃗S gleich der Zentrifugalkraft F⃗Z . Daraus ergibt sich:
Mit der Umdrehungszahl N in 1/min folgt hieraus:
In der Praxis nachteilig beim Watt/Boulton-Regler ist die Tatsache, dass sich der Winkel α schon bei relativ kleiner Drehzahl N dem Grenzwinkel von 90° annähert und die Höhendifferenz Δh sich nur für einen relativ kleinen Drehzahlbereich brauchbar zur Regelung verwenden lässt. In der Abblidung rechts ist dies für ein Beipiel dargestellt.
Bezieht man die Masse m der Hülse beim obigen Regler mit ein, so ergibt sich nach Herleitung unter Berücksichtigung der auftretenden Drehmomente [4] für den Winkel α:
Insbesondere wenn man die Masse m der Hülse signifikant erhöht, so ergibt sich ein deutlich größerer Bereich für die Regelung, wie dies in der Abbildung rechts exemplarisch dargestellt ist.
Porter-Regler
Genau diesen Effekt macht sich der Porter-Fliehkraftregler [5] zunutze.
![Fliehkraftregler nach Porter [5]](https://image.jimcdn.com/app/cms/image/transf/dimension=1920x400:format=jpg/path/scee86bccd27a6ab2/image/i65bdc1070fdb4125/version/1582974379/image.jpg)
Zum einen befindet sich auf der Hülse eine zusätzliche schwere zentrale Last. Zum anderen sind die Hebel anders angeordnet, und es gilt a = L. Somit ergibt sich für den Winkel α:
und für die Höhe h (N in 1/min):
d.h. die zur Regelung benötigte Höhe ist (1 + m/M)-mal größer als beim Watt / Boulton-Regler und eignet sich somit auch für höhere Drehzahlen (vgl. Abbildung rechts mit den obigen Diagrammen).
Eine Übersicht anderer Bauformen für Regler mit mathematischer Betrachtung findet man z.B. bei [4].
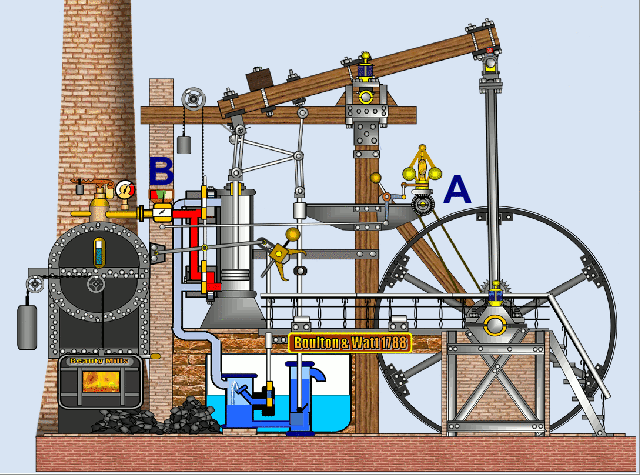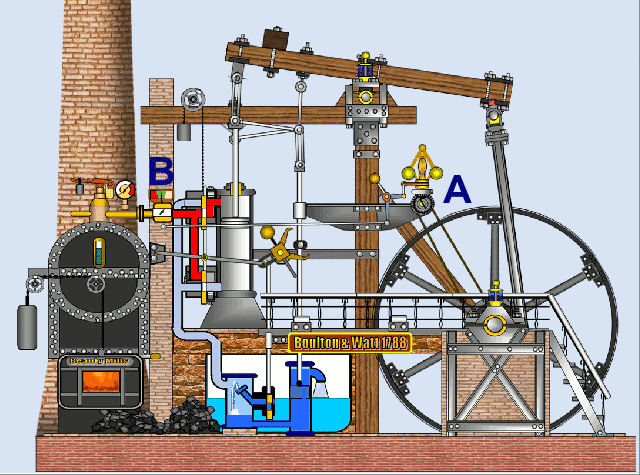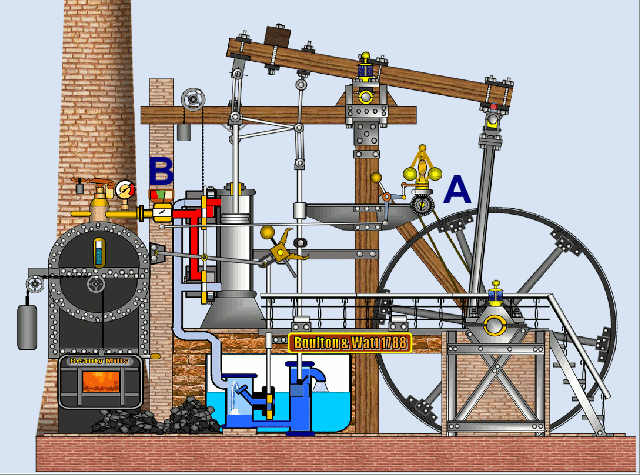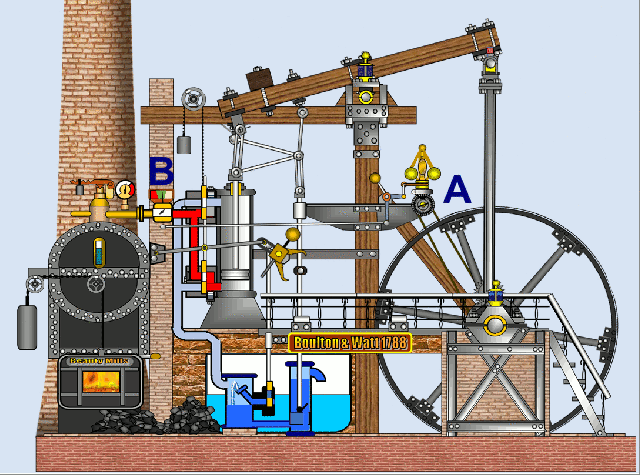
Abschließend noch ein animiertes Modell einer Dampfmaschine, das mit EXCEL und VBA [6] erstellt wurde. Hier "öffnet / schließt" der Watt / Boulton-Regler A über ein Gestänge das Dampfventil B.
Quellenverweise
[1] https://de.wikipedia.org/wiki/Matthew_Boulton
[2] Robert H. Thurston, A History of the Growth of the Steam-Engine (1886), S. 115,
http://www.gutenberg.org/files/35916/35916-h/35916-h.htm
[3] https://www.edumedia-sciences.com/de/media/642-dampfmaschine
[4] https://de.scribd.com/document/186855870/Governor-Student