3D Apfel

Eine Animation mit einer Rundumansicht des Apfels findet man unter Rotationen im Raum.

Der Apfel wird mit einer parametrischen Funktion und den Modellparametern R, r, h, k, d, D, L, s sowie einer Funktion für den Stiel erzeugt:

x (u,v) = cos (u) [R + r cos (v)] + d cos (D u)

y (u,v) = sin (u) [R + r cos (v)] + s (v / π)¹⁰

z (u,v) = h r sin (v) + k cos(v) + L stiel (v)

mit - π ≤ u, v ≤ π.

Ausgangspunkt ist ein Dorntorus (gelber Anteil), dessen Höhe mittels h gestreckt ist (linkes Bild).

Mit dem grünen additiven Anteil der z-Komponente und k wird eine "konische" Form erzeugt (rechtes Bild)

Die entstandene Form wird mit dem additiven Anteil der x-Komponente (orange) (wahlweise auch y-Komponente) deformiert: sie erhält "Beulen", deren Amplitude durch d und deren Anzahl durch D bestimmt ist.

Die Funktion stiel (v) wird zur z-Komponente addiert, um einen Stiel zu erzeugen:

Sie muss so beschaffen sein, dass sie nahe bei v = π (obere Mulde des Apfels) exponentiell ansteigt; auf diese Weise entsteht eine Art Röhre. Hierzu gibt es unterschiedliche Ansätze; einige Beispiele sind im folgenden Diagramm dargestellt.

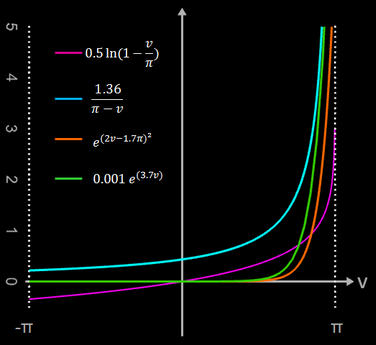
Um den Stiel schief zu stellen, wird bei der x- oder y-Komponente noch der oben angegebene Term (lila) addiert.Für Werte von v nahe π strebt dieser wegen des hohen Exponenten (gerade Zahl, mindestens 10) gegen 1 bzw. gegen s, sonst ist der Wert fast 0, wodurch eine Verzerrung der x-Werte im Bereich des Stiels erreicht wird und dieser somit schief steht.

Die folgende Tabelle enthält die Parameter für zwei Modelle, von denen das obere den oben abgebildeten Apfel erzeugt. Hierbei wurde der Bereich für v auf -3.1 bis 3.1 eingegrenzt, da der Stiel sonst gegen ∞ strebt.

Stiel-Funktion	R	r	h	k	d	D	L	s	v_min	v_max
1 / (π - v)	5	4.7 ... 5.0	6.6	2	0.25	5	1.36	1.25	-3.1	3.1
- ln (1 - v / π)	5	4.7 ... 5.0	5.8	2	0.25	5	2.4	1.14	-3.1	3.1

Abschließend zum Vergleich noch ein realer (https://commons.wikimedia.org/wiki/File:Apfel-Topaz.jpg) und ein mit dem 3D-Modell Apfel: