Explizite 3D Flächen (Funktionsgraphen)
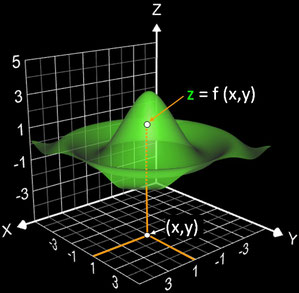
Explizite Flächen (Flächen in expliziter Darstellung) sind Funktionsgraphen einer Funktion f zweier Veränderlicher
Jedem Paar (x, y) bzw. Punkt (x | y) wird genau ein Wert z zugeordnet. Die explizite Fläche A enthält somit alle Funktionswerte von f:
A = { (x | y | z) | z = f (x, y) }
(vgl. Implizite Flächen; dort besteht die Fläche aus den Nullstellen einer Funktion in
impliziter Darstellung).
Wenn überhaupt ist die Untersuchung der Eigenschaften von Funktionen zweier Veränderlicher in der Schule Gegenstand in Mathematik-Leistungskursen aber definitiv an der Uni / Hochschule in Vorlesungen zur Analysis / Höhereren Mathematik.
Funktionen zweier Veränderlicher werden hier jedoch nicht weiter betrachtet; es werden lediglich einige Beispiele mit verschiedenen Darstellungsvarianten gezeigt.
Hingegen sind Funktionen in Parameterdarstellung wesentlich "leistungsfähiger" im Sinne, dass sie interessante Flächen erzeugen (s. Parameterflächen) und sich mit ihnen vielfältige 3D Objekte modellieren lassen (s. 3D Mathe). Insbesondere entfällt die Beschränkung der Funktionseigenschaft von f , nach der jedem Paar (x, y) genau ein Wert z zugeordnet ist; somit können in z-Richtung mehrere Teilbereiche der Fläche übereinander liegen.
Beispiele
f (x, y) = x³ - 3 x y²
f (x, y) = 2 sin (x) sin (y)
f (x, y) = 2 sin (x) sin (y)
Contour Plot
f (x, y) = | x y |
mit Höhenlinien
f (x, y) =
5 x² exp (-0.5 (x²+y²))
f (x, y) =
-√ |x| - √ |y| + 3
f (x, y) =
sin (y + cos (x)) / (y²+0.2)
f (x, y) =
3 sin ((x²+y²)²) / (x²+y²)²