3D Supershape

Eine weitere Superquadrik, das Supershape, beruht auf der Superformel von Gielis. Zur Herleitung wird zunächst das sphärische Produkt zweier Kurven definiert, wobei ich mich bei der Notation an Barr's Arbeit [1] halte. Auch das Superellipsoid und der Supertoroid basieren auf dem sphärischen Produkt. Eine kleine Übersicht findet man in [2].

Das sphärische Produkt zweier 2D-Kurven

ist definiert als

Dabei definiert der Vektor s eine geschlossene 3D-Fläche. Dies kann man sich geometrisch so vorstellen, dass eine horizontale Kurve h vertikal  längs der Funktion m verschoben wird, wobei m₁ (η) die Kurve h skaliert (man sagt dazu auch "moduliert"), während m₂ (η) die vertikale Schiebebewegung vorgibt. Somit beeinflusst ω die entstehende 3D-Fläche horizontal, η hingegen vertikal.

Im folgenden sind noch zwei weitere Beispiele für ein sphärisches Produkt dargestellt, wobei bei beiden die modulierende Kurve ein Halbkreis ist, gegeben durch

m₁ (η) = r cos (η)

m₂ (η) = r sin (η)    mit  - ½ π ≤ η ≤ ½ π.

Zur 3D Superformel gelangt man, indem man für m einen Halbkreis mit dem Radius r_m, für h einen Kreis mit dem Radius r_h nimmt und einen der Radien oder beide durch eine bzw. zwei Superformeln sf₁, sf₂ ersetzt
(s. Diverse Themen/Superformel).

Die Graphing Calculator 3D-Datei im Download-Bereich leistet genau das; hierzu ein Beispiel:

Zunächst legt man die Superformeln sf₁ und sf₂ fest und lässt sie sich anzeigen.

• sf₁ : a = 1,  b = 1,  m₁ = m₂ = 5,  n₁ = 0.5,  n₂ = 0.5,  n₃ = 0.5   
• sf₂ : a = 1,  b = 1,  m₁ = m₂ = 2,  n₁ = 1,  n₂ = 1,  n₃ = 1  

Mit einem Slider stellt man den Typ der entstehenden 3D Superformel ein:

Hier noch ein weiteres Beispiel mit den Superformeln

• sf₁ : a = 1,  b = 1,  m₁ = 2,  m₂ = 10,  n₁ = -1.5,  n₂ = 1,  n₃ = 1  
  
• sf₂ : a = 0.8,  b = 3,  m₁ = m₂ = 6,  n₁ = -0.25,  n₂ = 1,  n₃ = 1 
  

und den entstehenden Objekten (Typ 0 bis Typ 3):

Im folgenden noch ein paar weitere Beispiele von Supershapes (das Problem dabei ist, dass ich mich kaum entscheiden kann, welches denn nun gezeigt werden soll - sobald man die Reglern des Programms bewegt, entstehen ja stets neue Formen - ein weiterer Grund, es mit Graphing Calculator 3D einmal selbst zu versuchen):

Die x-, y- und z-Komponente des Supershapes können noch mit einem Vektor [ r_x, r_y, r_z ] multipliziert werden, wobei das Supershape dann in x-, y-, z-Richtung für r-Werte > 1 gestreckt, für r-Werte < 1 gestaucht wird.

Bei der folgenden "Blumengalerie" wurde davon Gebrauch gemacht (r<1 für die z-Komponente), um flache Blüten zu erzeugen.

Weitere Beispiele mit dieser Technik sind 3D Herzen; Sie finden diese unter 3D Mathe/3D Objekte/3d Herz.

Eine Variante zur Erzeugung von Supershapes besteht darin, anstelle des spärischen Produkts einen Torus zu verwenden, wobei der äußere Radius R sowie der innere Radius r des Torus durch die Superformeln sf₁ und sf₂ ersetzt werden:

Torus:

x (u, v) = cos (v) [ R + r cos (u) ]                  x (u, v) = cos (v) [ sf₁ (v) + sf₂ (u) cos (u) ]

y (u, v) = sin (v)  [ R + r cos (u) ]        →       y (u, v) = sin (v)  [ sf₁ (v) + sf₂ (u) cos (u) ]      mit  0 ≤ u, v ≤ 2π

z (u,v) = r sin (u)                                            z (u,v) = sf₂ (u) sin (u)

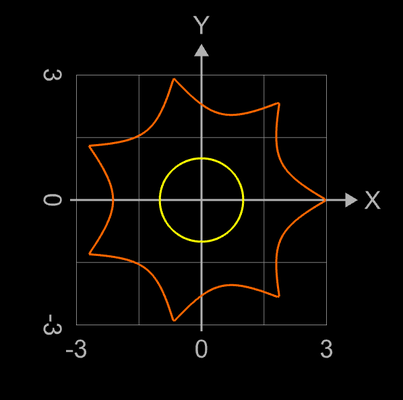
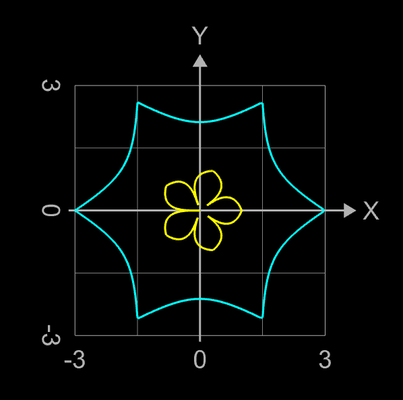
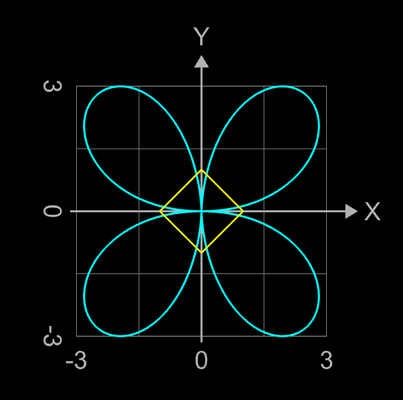
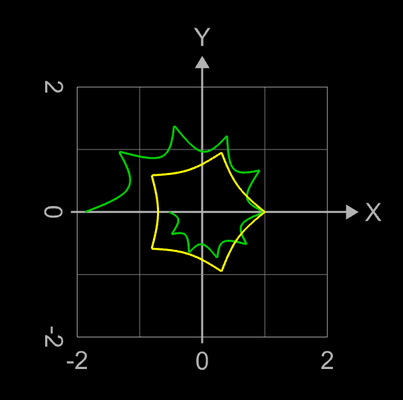
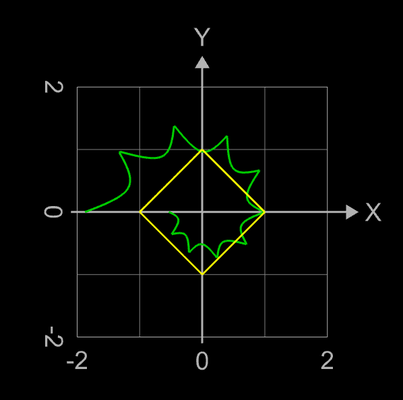
Somit bestimmen sf₁ die äußere Form (Umriss) des Torus und sf₂ seinen Querschnitt.

Einige Besipiele sind in der nachfolgenden Bildergalerie zusammengestellt. Diese wurden mit der oben genannten Graphing Calculator 3D-Datei erzeugt, bei der das sphärische Produkt durch die obigen Toruskomponenten ausgetauscht wurde. Die 2D-Diagramme zeigen dann die äußere Form sowie den Querschnitt (in gelb) des entstehenden Torus.

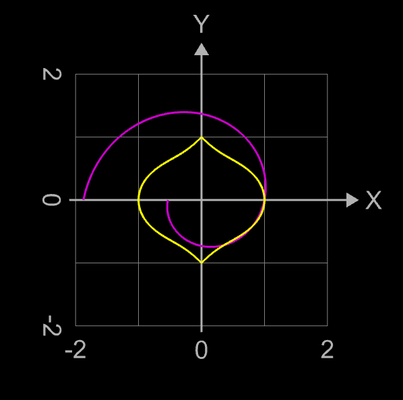
Bei den obigen "Spiralen" wurde die ursprüngliche Superformel sf₁ (φ) noch mit e ^{c φ} multipliziert
(hier: c = 0.2) (vgl. 2D-Mathe/2D-Superformel). 

Quellenverweise

[1]   Superquadrics and Angle-Preserving Transformations   (PDF)

[2]   On Spherical Product Surfaces in E3   (PDF)

Download