Übergangskurven
Mit Hilfe von Übergangskurven (in parametrisierter oder expliziter Darstellung) lassen sich zwei Kurven verbinden. Eine typische
Anwendung findet man im Straßen- und Gleisplanung, wobei z.B. Streckenelemente wie Geraden und Kreisbögen mit Hilfe einer Klothoiden an andere Streckenelemente anschließen (s. Trassierung). Eine ähnliche Problemstellung mit Geraden und Kreisbögen als Übergang finden Sie bei Kreise verbinden.
Implizite Übergangskurven
Im Bereich des Computerdesigns verwendet man als Übergangskurven vorzugsweise implizite Kurven, um die geometrische Stetigkeit (Begriff aus der Geometrischen Modellierung [1]) zu realisieren, wobei insbesondere die G2-Stetigkeit angestrebt wird, d.h. dass unabhängig von der Darstellungsart (parametrisiert, implizit, explizit) Übergangskurve und Objektkurve im Berührpunkt dieselbe Tangente und dieselbe Krümmung haben.
Als Beispiel hierfür dienen zwei Kreise in impliziter Darstellung (s. Animation):
f1 (x, y) = (x - x1)² + y² - r1²
f2 (x, y) = (x – x2)² + y² - r2²
liefert z.B. die einfache Konstruktion [2]
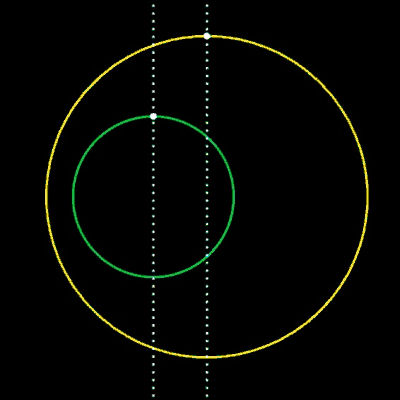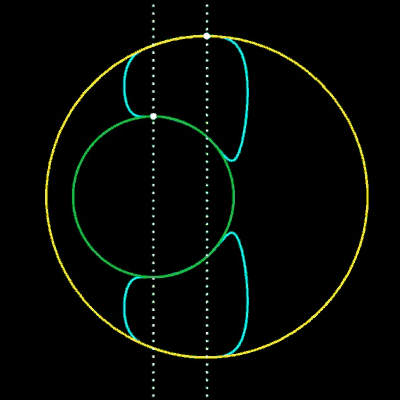
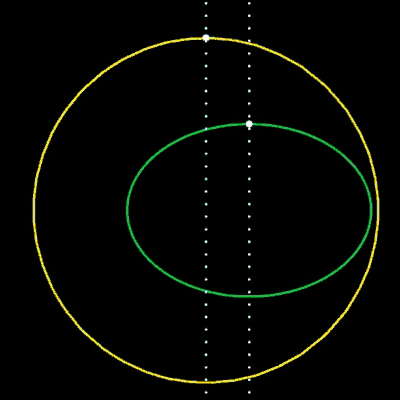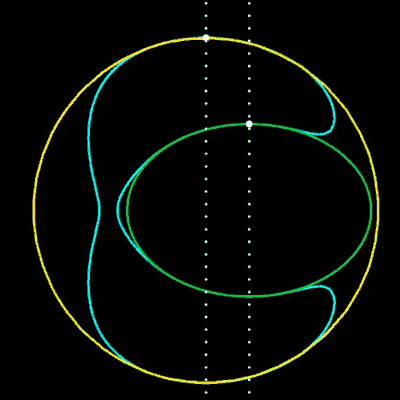
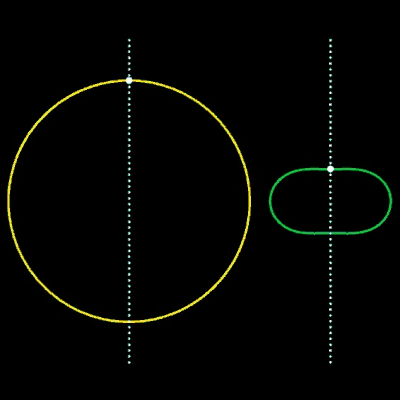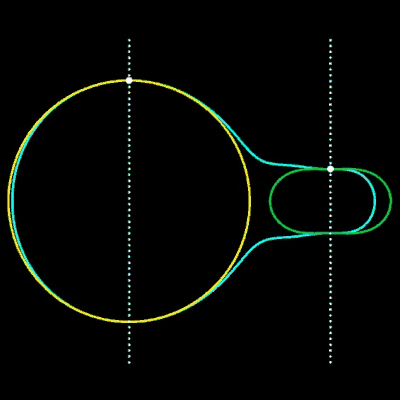
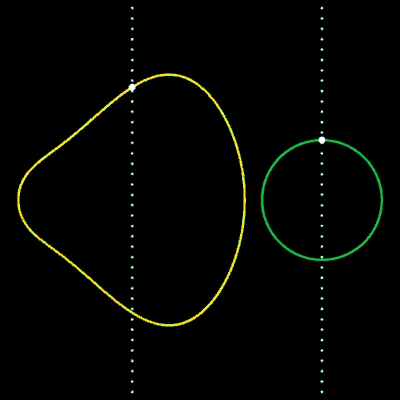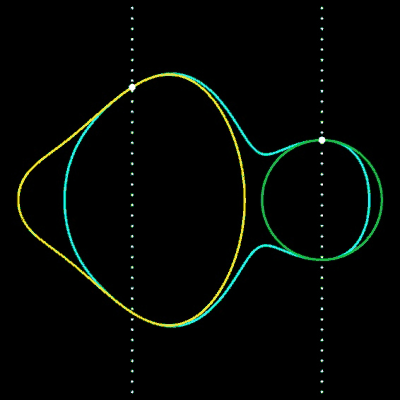
F (x, y) = (1 - µ) f1 f2 + µ (g1 g2)³
krümmungsstetige Übergangskurven zwischen beiden Kreisen. Die beiden Geraden
g1 (x, y) = x - x1 = 0
g2 (x, y) = x - x2 = 0
bestimmen die Berührpunkte P1 und P2 (•) der cyan-farbenen Übergangskurven an den Kreisen, wobei als Übergangskurven nur die mittleren Kurventeile dienen.
Hierbei ist der Parameter µ ein Design-Parameter. Wären Kreise und Übergangskurve Straßen, so könnte ein Fahrzeug ohne Ruck entlang der Übergangskurve von einem auf den anderen Kreisbogen fahren.
Für die Animation wurden folgende Größen gewählt: x1 = -2, r1 = 2, x2 = 3, r2 = 1, µ = 0.07 … 0.17.
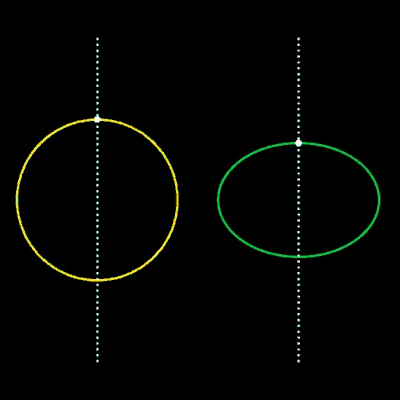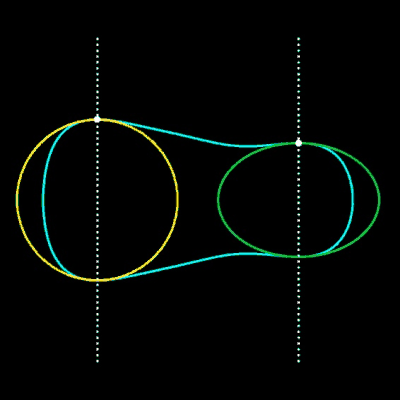
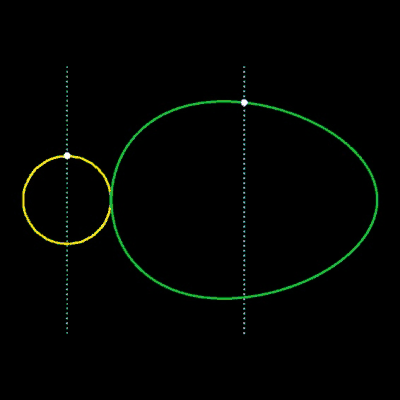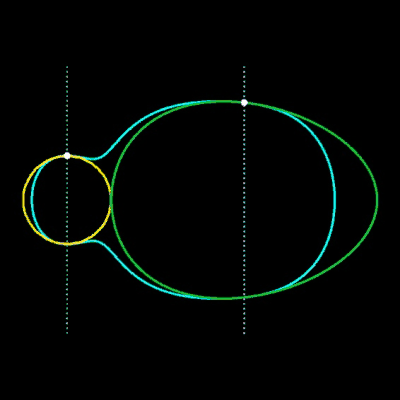
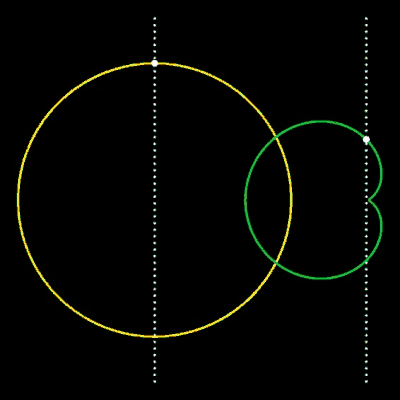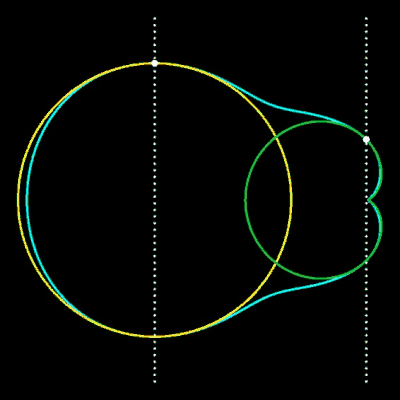
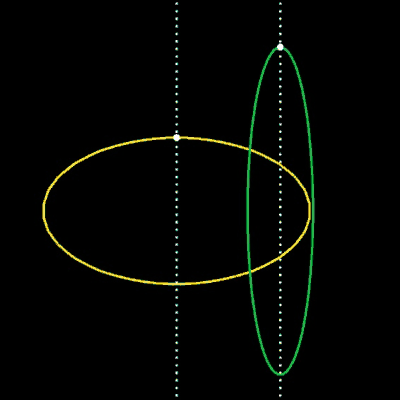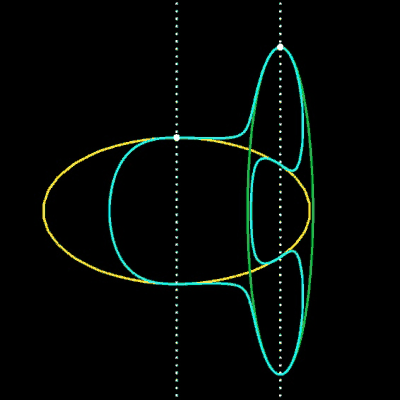
Die obige Übergangsfunktion F lässt sich auch auf andere implizite Kurven übertragen. Einige Beispiele hierfür finden Sie in den folgenden Grafiken.
Übergangskurve Kreis <> Kreis
Kreis1: f1 (x, y) = (x - x1)² + y² - r1²
Kreis2: f2 (x, y) = (x – x2)² + y² - r2²
Übergangskurve Kreis <> Ellipse 1
Kreis: f1 (x, y) = (x - x1)² + y² - r1²
Ellipse: f2 (x, y) = a (x – x2)² + y² - r2
Übergangskurve Kreis <> Ellipse 2
Kreis: f1 (x, y) = (x - x1)² + y² - r1²
Ellipse: f2 (x, y) = a (x – x2)² + y² - r2
Übergangskurve Kreis <> Ei
Kreis: f1 (x, y) = (x - x1)² + y² - r1²
Ei: f2 (x, y) = a-² (x - x2)² + b-² y² (1+c (x - x2))
Übergangskurve Kreis <> Cassini
Kreis: f1 (x, y) = (x - x1)² + y² - r1²
Cassini: f2 (x, y) = ((x - x2)² + y²)² - 2c² ((x - x2)² -
y²)
-
(a4 - c4)
Übergangskurve Kreis <> Kardiode
Kreis: f1 (x, y) = (x - x1)² + y² - r1²
Kardiode: f2 (x,y) = ((x - x2)² + y²)²
+ 4a (x -
x2)((x - x2)² + y²) - 4a² y²
Übergangskurve Objekt <> Kreis
Objekt: f1 (x, y) = (x - x1)² + y² + sin (-2 (x - x1)) - 2.5
Kreis: f2 (x, y) = (x – x2)² + y² - r2²
Übergangskurve Ellipse <> Ellipse
Ellipse1: f1 (x, y) = 0.3 (x - x1)² + y² - r1
Ellipse2: f2 (x, y) = 5 (x – x2)² + 0.2 y² - r2