Verfolgungsproblem (Käfer, Mäuse)

Vier Käfer sitzen in den Ecken eines Quadrates (s. Grafik rechts) und laufen mit gleicher Geschwindigkeit gleichzeitig los. Käfer 1 läuft in Richtung Käfer 2, Käfer 2 in Richtung Käfer 3, Käfer 3 in Richtung Käfer 4 und dieser in Richtung Käfer 1. Auf welchem Weg, welchen Kurven bewegen sich die Käfer?

Dieses Problem stellte M. Gardner 1957 u.a. in der Zeitschrift Scientific American vor [1]. Es ist jedoch nicht neu, denn solcherlei Verfolgungs-probleme wurden bereit Ende des 19. Jahrhunderts diskutiert, wenn auch zunächst mit einem gleichseitigen Dreieck statt einem Quadrat.

Im Laufe der Zeit änderten sich auch die "Teilnehmer", wie z.B. Hunde, Jungen, Käfer, Mäuse, Teilchen. In [2] findet sich ein ausführlicher historischer Überblick über solche zyklischen Verfolgungsprobleme.

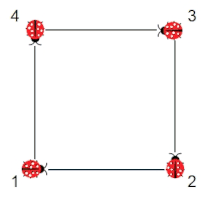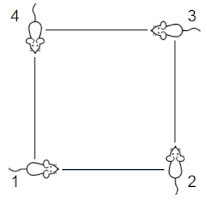
Verfolgungsproblem (Käfer, Mäuse) Ausgangssituation — Verfolgungsproblem (Käfer, Mäuse)

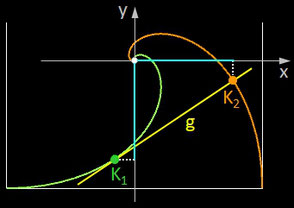
Für das zuvor beschriebene Problem soll nun die Bahnkurve eines Käfers bestimmt werden. Der Mittelpunkt des Quadrats mit einer Kantenlänge 2 befinde sich im Ursprung eines Koordinatensystems, die Positionen der Käfer zu Beginn seien die Eckpunkte (-1 | -1), (1 | -1), (1 | 1) und (-1 | 1) des Quadrats.

Zu einem beliebigen Zeitpunkt befinde sich Käfer 1 im Punkt K₁(x | y). Käfer 2 befindet sich dann aus Symmetriegründen im Punkt K₂(-y | x) (s. Grafik rechts).

Die Gerade g (K₁K₂) ist die Tangente in K₁ an die gesuchte Kurve von Käfer 1. Mit der Steigung der Tangente ergibt sich somit die Differentialgleichung (DGL)

Mit Polarkoordinaten gilt x = r ∙ cos(φ) und y = r ∙ sin(φ).

zur Bestimmung der Bahnkurve von Käfer 1

Mithin ist

Einsetzen in die obige DGL ergibt dann eine DGL für r in Abhängigkeit von φ, die es zu lösen gilt:

Setzt man für die Bestimmung der Konstanten C die Anfangsbedingung r = √2 und φ = 5/4π für Käfer 1 ein, so erhält man schließlich die Bahnkurve von Käfer 1 – eine logarithmische Spirale:

Die nebenstehende Animation zeigt die Lösung des Problems mit vier Käfern, die sich auf vier kongruenten Logarithmischen Spiralen aufeinander zu bewegen und sich im Mittelpunkt des Quadrats treffen.

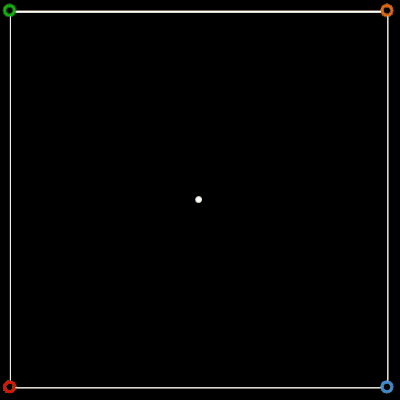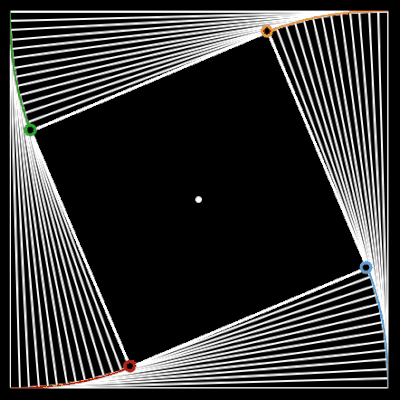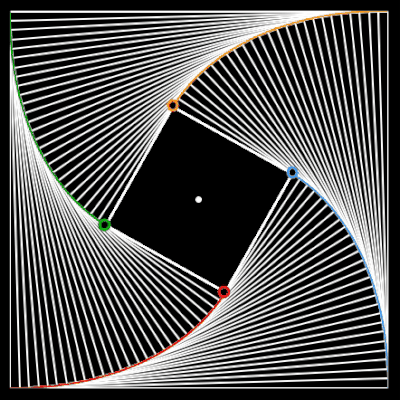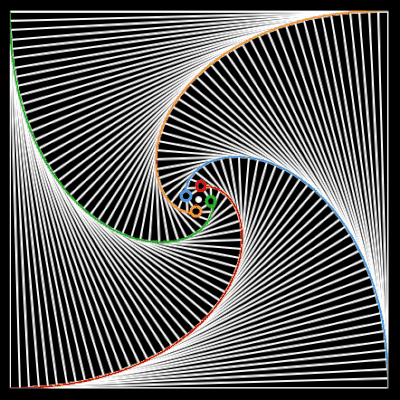
Verbindet man zu einem beliebigen Zeitpunkt die Orte der Käfer durch Geraden, so entsteht ein verkleinertes Ausgangspolygon (Quadrat). Die Folge dieser immer kleiner werdenden Quadrate bildet einen Wirbel (engl. whirl) [ ], wobei die Ecken der Quadrate die Bahnen (Logarithmische Spiralen) bilden (s. folgende linke Animation). Eine ähnliche Figur kann mit der Gielis-transformierten Logarithmischen Spirale

mit m = 4.10404 erzeugt werden (s. folgende rechte Animation sowie 2D Mathe/ 2D Superformel - 2).

Die Herausgeber des Scientific American erkannten die Popularität der Thematik und widmeten dieser ein entsprechendes Titelbild (s. rechte Grafik in folgender Galerie).

entstehender Wirbel beim Verfolgungsproblem mit n=4 Käfern (Mäusen)

Wirbelbildung bei Gielis-transformierter Logarithmischer Spirale mit rationalem m

Titelseite des Scientific American Juli 1965

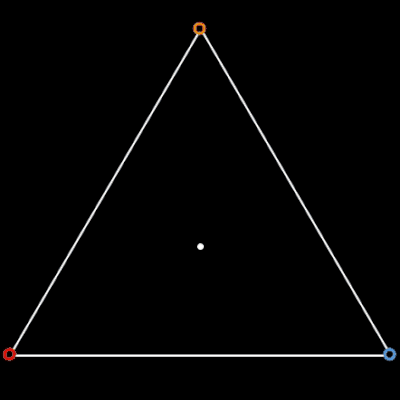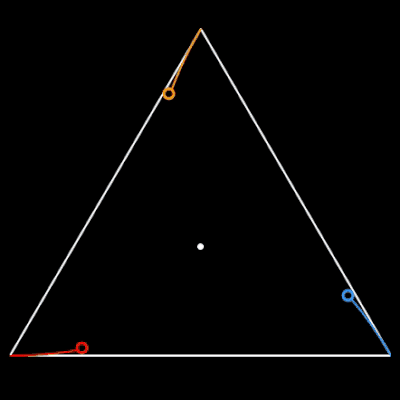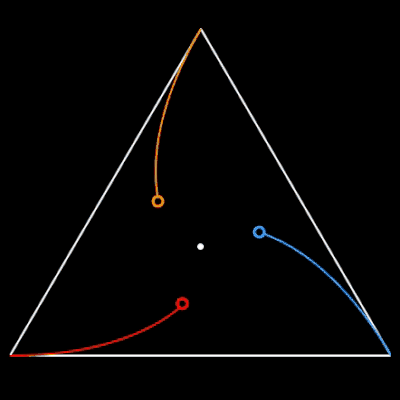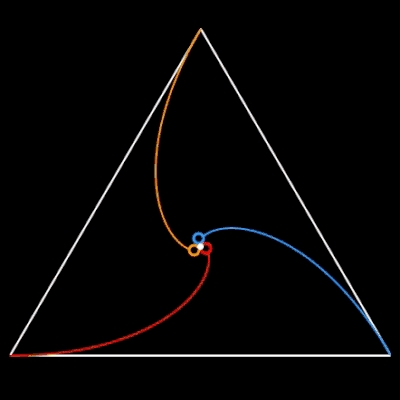
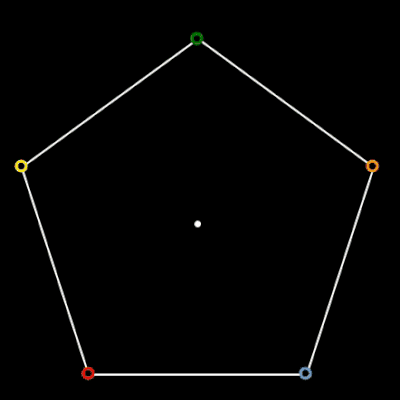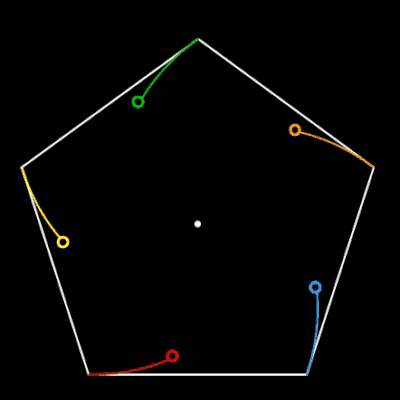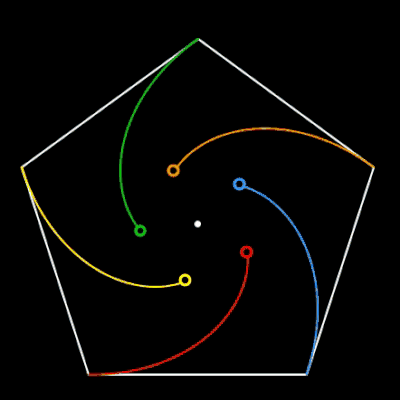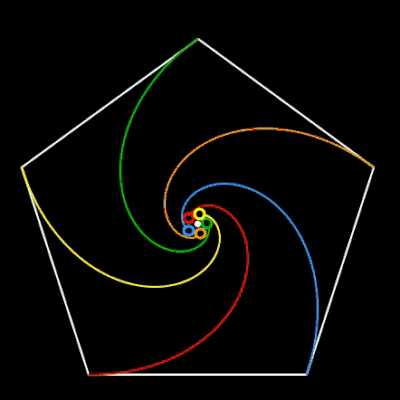
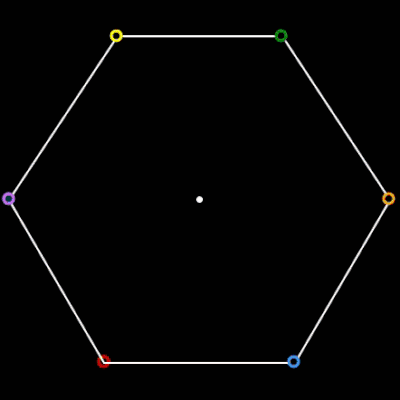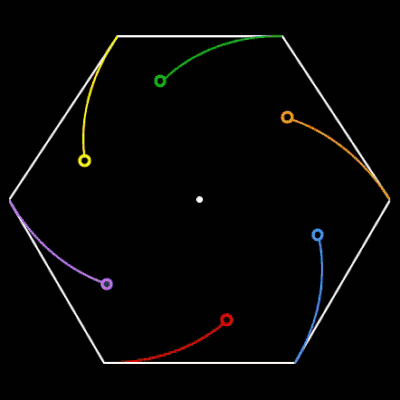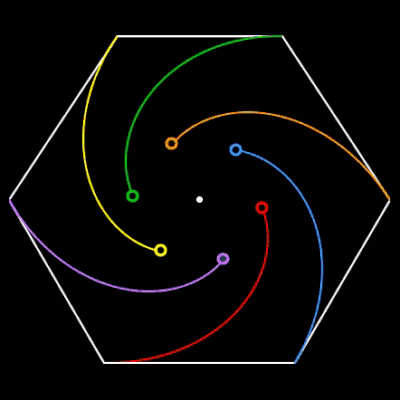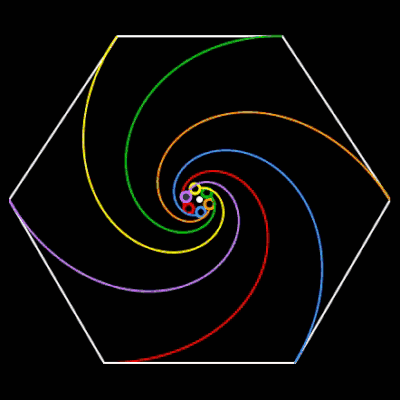
Für n = 3, 5 und 6 sich verfolgende Objekte auf den Ecken des jeweiligen n-Polygons habe ich das zyklische Verfolgungsproblem einmal mit EXCEL nachgestellt:

Aufgrund von Anwendungen in der Robotik und der Verfügbarkeit leistungsfähigerer Computer hat das Interesse am n-Käfer-Problem und verschiedenen Verallgemeinerungen (z.B. unregelmäßige Polygone, unterschiedliche Geschwindeigkeiten der Käfer) in den letzten beiden Dekaden anscheinend wieder zugenommen, siehe z.B. [4] bis [9].

Quellenverweise

[1] M. Gardner (1957) Mathematical Games. Nine titillating puzzles, the answers to which will be given
next month, Sci. Am. 197, 140–146 (doi:10.1038/scientificamerican1157-140)

[2] P. J. Nahin (2012) Chases and Escapes: The Mathematics of Pursuit and Evasion,
Princeton University Press, S. 106 – 110, https://muse.jhu.edu/book/30498

[3] https://mathworld.wolfram.com/Whirl.html

[4] S. J. Chapman, J. Lottes, L. N. Trefethen (2011) Four bugs on a rectangle,
Proc. Roy. Soc. A (2011) 467 881-896, doi: 10.1098/rspa.2010.0506

[5] K. S. Galloway, E. W. Justh, P. S. Krishnaprasad (2013), Symmetry and reduction in collectives: Cyclic
pursuit strategies, Proc. Roy. Soc. A 469.2158, DOI:10.1098/rspa.2013.0264

[6] T. J. Richardson (2001) Non-mutual captures in cyclic pursuit, Annals of Math. and Art. Intel. 31(1-4)
127–146, DOI:10.1023/A:1016670220800

[7] T. J. Richardson (2001) Stable polygons of cyclic pursuit, Ann. Math. Art. Intel. 31(1–4) 147–172,
DOI:10.1023/A:1016678406688

[8] J. Yu, S. M. LaValle, D. Liberzon (2008) Rendezvous without coordinates,
47th IEEE Conference on Decision and Control, CDC, Cancun, Mexico

[9] J.A. Marshall (2005) Coordinated Autonomy: Pursuit Formations of Multivehicle Systems, PhDThesis,
University of Toronto, Ontario, Canada, http://individual.utoronto.ca/marshall/docs/phdthesis.pdf