Klothoide (Cornu-Spirale, Euler-Spirale)
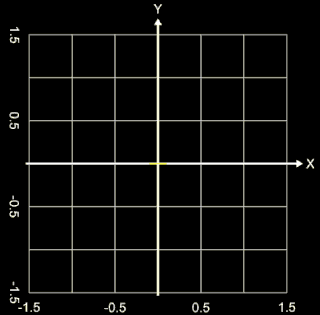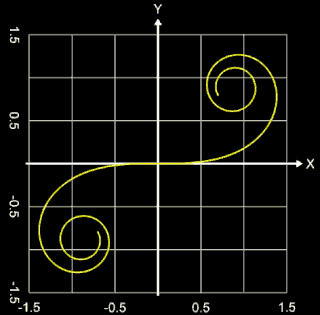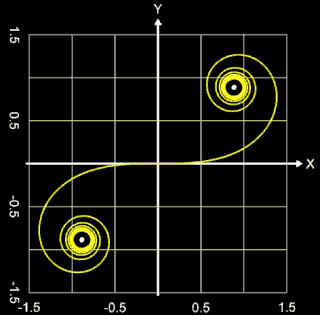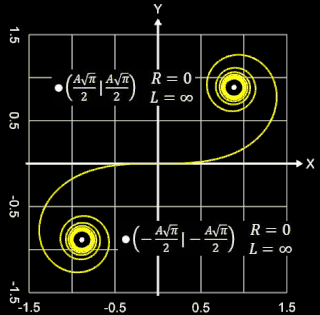
Die Klothoide (griechisch κλώθω für "spinnen"), auch Cornu- oder Euler-Spirale genannt, ist eine ebene Kurve, die dadurch eindeutig bestimmt ist, dass an jeder Stelle der Kurve die Krümmung proportional zur Länge ihres Bogens bis zu der Stelle ist. Die Klothoide wird auch "Spinnkurve" genannt, da mit zunehmender Länge L die beiden Konvergenzpunkte
"umsponnen" werden.
Wie bereits oben erwähnt, ist bei einer Klothoide die Krümmung κ
proportional zum durchlaufenden Bogen L:
d.h. je länger der Klothoidenbogen wird, umso stärker ist er gekrümmt - was gleichbedeutend ist mit - umso kleiner wird der Radius R des Krümmungskreises wie in der Animation rechts
dargestellt (zum Begriff Krümmung und Krümmungskreis s. auch die entsprechenden Abschnitte unter Trassierung).
Die positive Konstante A ist der Klothoidenparameter.
Im folgenden wird die Gleichung für die Klothoide hergeleitet ...

Für jeden Punkt P der Klothoide mit dem dortigen Radius R und der Länge L vom Ursprung bis zu P gilt
Dazu betrachte man die folgende Grafik. Differentiell gilt hier
Integration der letzten Gleichung führt zu
Weiterhin gilt (s. Grafik)
Durch Integration erhält man schließlich die x- und y-Koordinaten der Klothoide mit der Länge L:
Die beiden Integrale sind nicht geschlossen lösbar, es handelt sich hier um Fresnel-Integrale, die "exakt" nur numerisch gelöst werden können (s. Fresnel-Integrale).
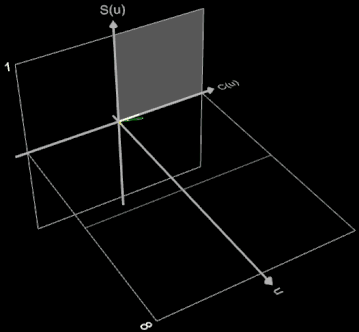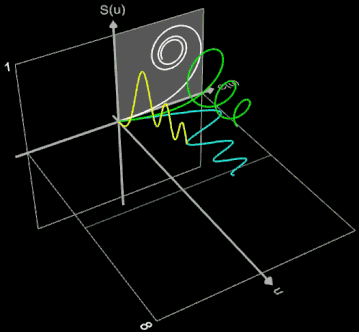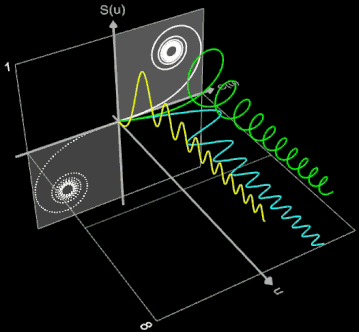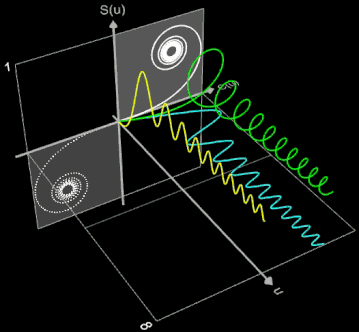
Zur weiteren Veranschaulichung diene die nebenstehende Animation. Die Integrationsvariable u in den Fresnel-Integralen
die die Punkte der Klothoide ergeben, wird als dritte räumliche Koordinate eingeführt. Somit ist die entstehende Cornu-Spirale eine Raumkurve im S(u)-C(u)-u-Koordinatensystem. Durch Parallelprojektion dieser Raumkurve in die S(u)-u-Ebene und in die C(u)-u-Ebene entstehen die Funktionsgraphen für S(u) und C(u). Die Parallelprojektion der Raumkurve in die S(u)-C(u)-Ebene ergibt die Klothoide (weiß). Für negative Werte von u ist die Klothoide im dritten Quadranten fortgesetzt (gepunktet).
Einheitsklothoide und Ähnlichkeit
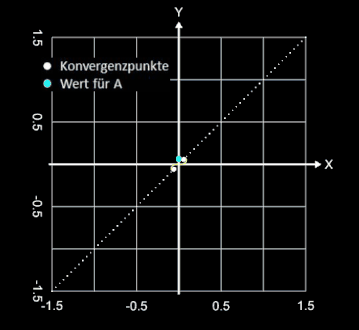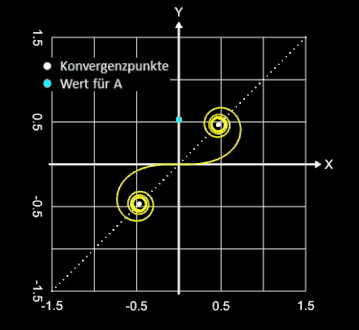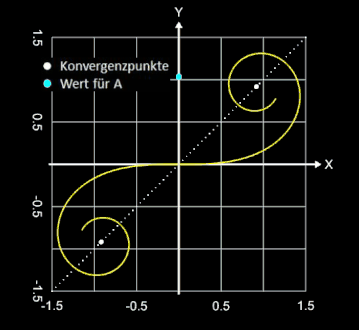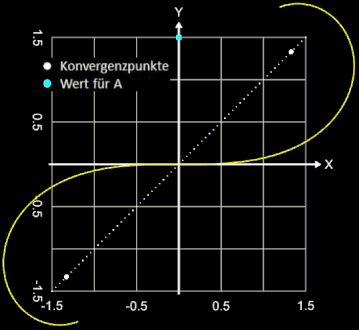
Mit A = 1 und folglich L • R = 1 ergibt sich die sogenannte Einheitsklothoide (s. oberste Grafik auf dieser Seite). Die Einheitsklothoide ist das Pendant zum Einheitskreis.
Jede Klothoide ist der Einheitsklothoide geometrisch ähnlich [ ], wobei A der Ähnlichkeitsfaktor (Vergrößerungsfaktor) ist (s. Grafik rechts).
Diese Tatsache machte man sich früher zunutze, indem man die Einheitsklothoide tabellierte und dann die benötigten Werte geeignet skalierte. Es genügte also, den Parameter A zu bestimmen und dann sämtliche Maßzahlen damit zu multiplizieren. Die Winkel bleiben bei der Skalierung erhalten.
Ein komplettes Beispiel von 1951 für die Berechnung einer Klothoide als Übergangbogen im Straßen-verkehr (s. Trassierung) mit Hilfe von Tabellen findet man in [2]. Heute ist diese Vorgehensweise nicht mehr nötig, da mit Hilfe von Software beliebige Klothoiden direkt berechnet werden können; Klothoiden sind als Objekte heutzutage in jeder CAD-Software vorhanden.
Allgemeine Klothoide
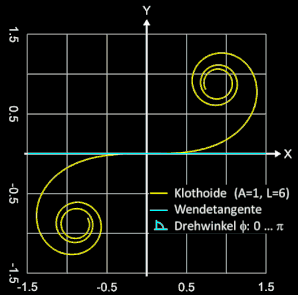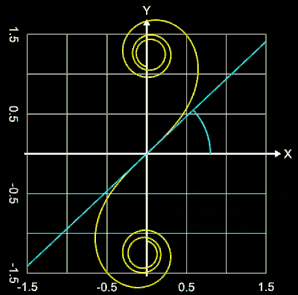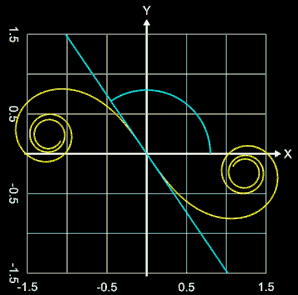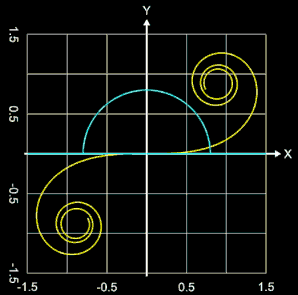
Die bis dato betrachtete Klothoide hat in (0 | 0) einen Wendepunkt. Ihr "Startwinkel" θ (= Winkel der Wendetangente) ist 0°. Um auch andere Winkel für θ zu realisieren, werden die oben hergeleiteten Gleichungen für die x- und y-Parameter der Klothoide entsprechend angepasst:
In der folgenden Animation rechts durchläuft θ die Werte 0 ... 180° bzw. 0 ... π in Bogenmaß.
Um eine "allgemeine" Klothoide mit den Basisparametern A und L darzustellen, werden die beiden obigen Gleichungen nochmals erweitert:
Hierbei bedeuten:
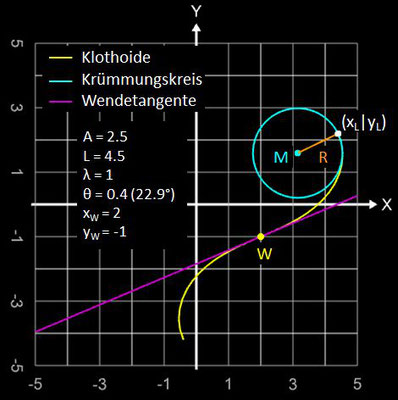
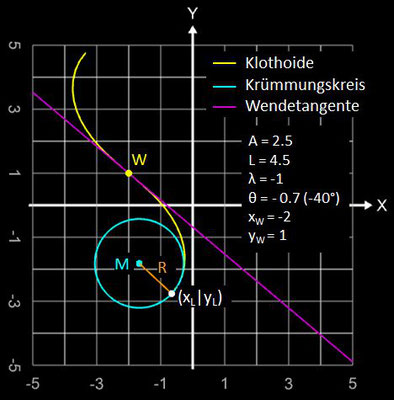
xw : x-Koordinate des Wendepunktes
yw : y-Koordinate des Wendepunktes
λ : Orientierung ("Spinnrichtung") der Klothoide (-1: im Uhrzeiger,sinn, 1: gegen Uhrzeigersinn)
θ : positiver Startwinkel (Winkel der Wendetangente) (-π … π)
Dazu hier zwei Beispiele:
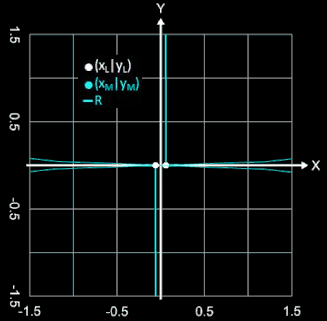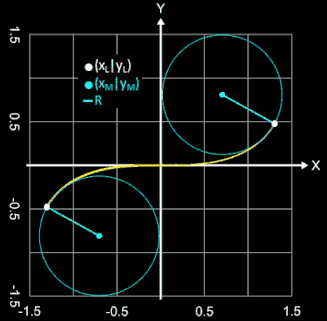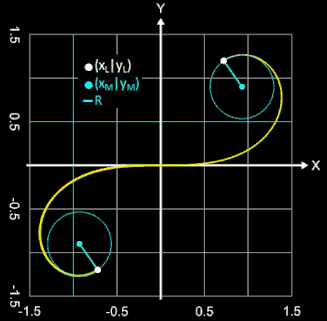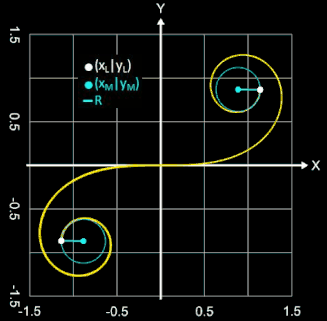
Die Datei für den Graphing Calculator 3D unten im Download-Bereich berechnet und stellt die allgemeine Klothoide mit A, L und obigen Parametern dar und ebenso den Krümmungskreis mit Radius R an einem Ende der Klothoide sowie die Wendetangente. Die hierfür erforderlichen Formeln ergeben sich zu:
• Radius R des Krümmungskreises:
• Mittelpunkt M (xM | yM) des Krümmungskreises:
• Radius R als Vektor zwischen M und (xL | yL):
• Wendetangente:
• Tangente in (xL | yL):
Klothoide mit alternativer Parametrisierung
Eine interessante Alternative zur Berechnung der Koordinaten eine Klothoide findet man bei [5]. Als numerische Lösung für ein zuvor aufgestelltes Anfangswertproblem gelangen die Verfasser zu folgendem Iterations-verfahren mit i = 0, ..., N-1:
mit xL ≈ xN und yL ≈ yN.
Wichtig bei diesem Iterationsverfahren ist die Wahl hinreichend großer Werte für N. Zum einen sind die Abweichungen von den exakten Werten xL und yL der Klothoide mit der Länge L umso geringer, je größer der Wert für N ist. Zum anderen kann es bei großen Längen L der Klothoide und nicht hinreichend großem N zu "Artefakten" kommen.
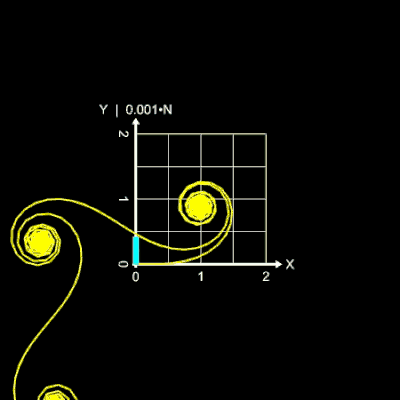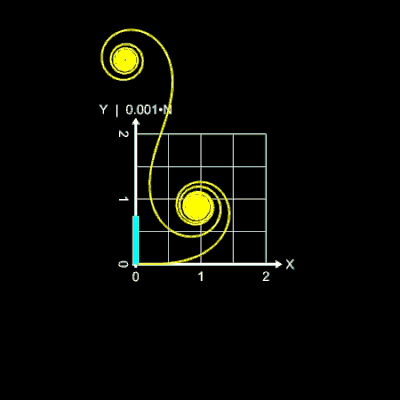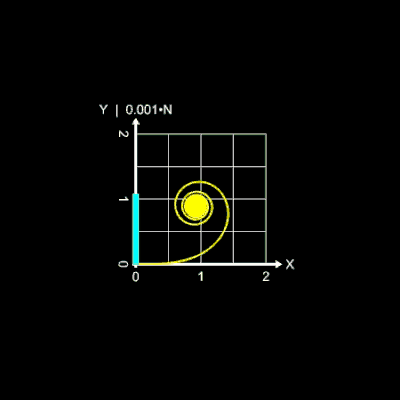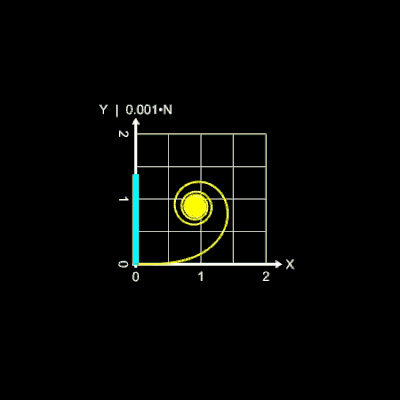
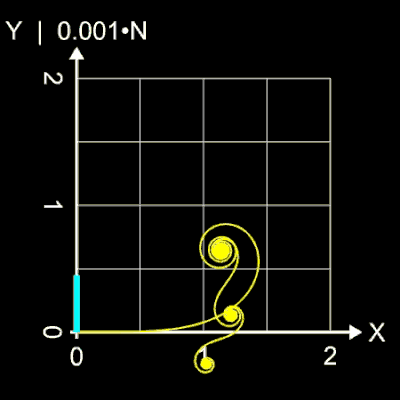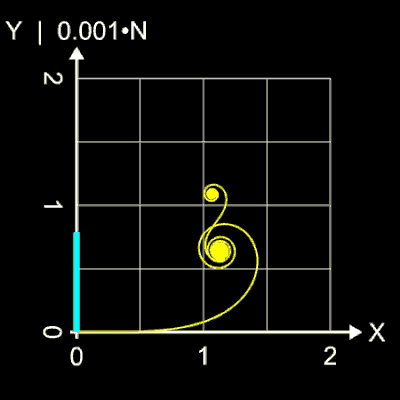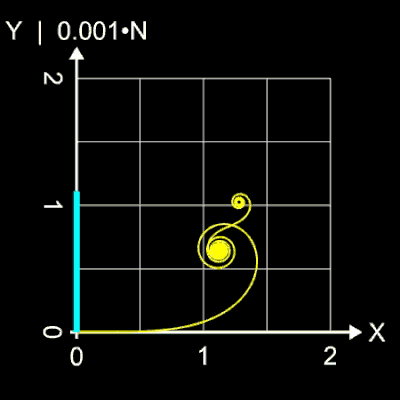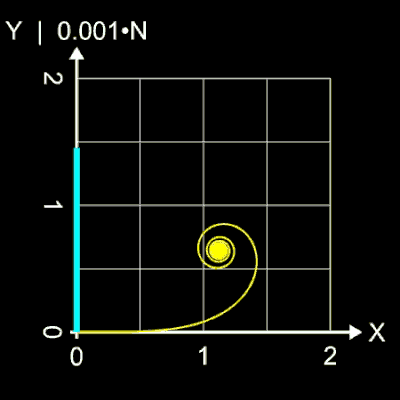
Die folgende linke Animation zeigt dies am Beispiel des positiven Astes der Einheitsklothoide mit L = 80. Hier durchläuft die Anzahl N der Iterationsschritte die Werte von 400
bis 1400, dargestellt durch den blauen Balken auf der y-Achse. Erst ab einem Wert von N = 1200 nähert sich die Klothoide der korrekten Form.
Bei Verwendung des Verfahrens für Polynomiale Cornu-Spiralen zeigt sich auf Grund der höheren Potenzen der Effekt bei gleichen Werten von N schon für deutlich kleinere Werte von L. Dies zeigt die rechte Animation am Beispiel der Polynomialen Cornu-Spirale mit dem Polynom p (t) = t³/3 mit L = 20.
Auf Grund der deutlich geringeren Komplexität der Iterationsvorschrift ist das Verfahren um ein Vielfaches schneller als die numerische Berechnung der Fresnel-Integrale, wie z.B. mit der Summierten Simpson-Regel (s. Numerische Integration).
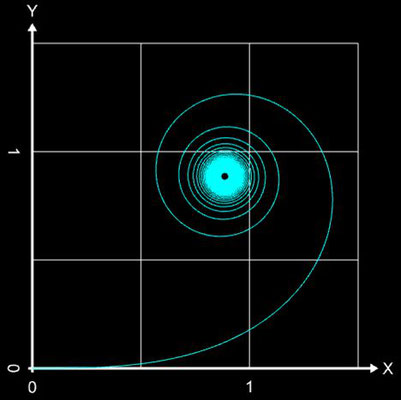
So wurde beispielsweise für A = 1 und L = 50 die Klothoide im folgenden linken Bild (gelb) mit der "alternativen Parametrisierung" in ca. 1 Sekunde berechnet (2000 Bildpunkte). Mit N = 106 beträgt die Abweichung z.B. für die x-Koordinate xL - xN ≈ 0.000442. Die "identische" Klothoide im mittleren Bild (cyan) wurde per numerischer Lösung der Fresnel-Integrale berechnet. Um die gleiche Genauigkeit zu erzielen, wurde dazu in der Summierten Simpson-Regel der Wert für n auf 745 gesetzt. Die Rechenzeit betrug 154 Sekunden (!).
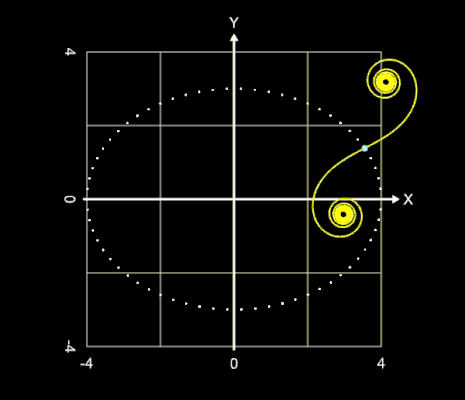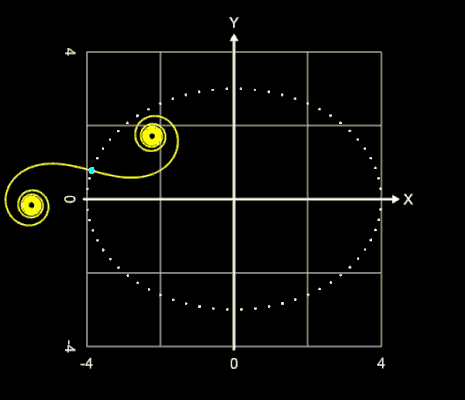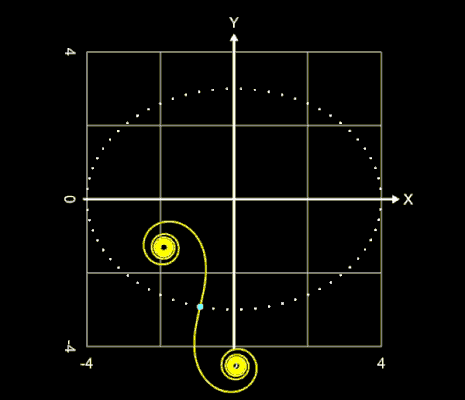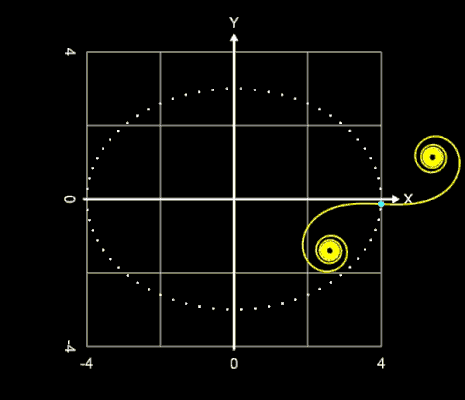
Die Animation in der obigen Galerie ist ein "Live-Mittschnitt" und zeigt eindrucksvoll die Geschwindigkeit beim Berechnen/Plotten einer Klothoide mit der alternativen Parametrisierung. Hierbei sind A = 1.5 und L = 20, die Größe φ wurde animiert (φ = 0 … 2π) und es wurde θ = φ gesetzt. Der Wendepunkt (xW | yW) bewegt sich auf einer Ellipse mit xW = 4 cos (φ), yW = 3 sin(φ).
Setzt man das Verfahren bei der Berechnung von Klothoiden im Straßenbau ein (s.u.), so sollte man N = 106
verwenden, damit z.B. für A = T = L = 3000 m die Abweichungen im Millimeterbereich liegen. Die Rechenzeit auf meiner Kombination aus Hardware und dem Graphing Calculator 3D (s. Tools) beträgt dann 6 Sekunden.
Hier hat mit einer Rechenzeit unter 1 Sekunde die numerische Berechnung der Fresnel-Integrale eindeutig die Nase vorn, ebenso wie die Anwendung von Näherungsformeln (s.u.) mit einer Rechenzeit im Millisekundenbereich.
Eine Verallgemeinerung der Klothoide / Cornu-Spirale erhält man, indem man in den Integralen die Argumente der Sinus- und Cosinus-Funktion durch ein Polynom ersetzt; dies führt zur polynomialen Cornu-Spirale.
Näherungsformeln für die Anwendung im Straßenbau
Klothoiden werden insbesondere als Übergangsbögen zwischen Geraden und Kreisbögen im Straßenbau eingesetzt (s. auch Trassierung, unterer Seitenabschnitt). Heutzutage sind Klothoiden als Objekte in jeder CAD-Software vorhanden. Darüber hinaus gibt es speziell angepasste Software-Module, wie z.B. für den Straßenbau. Bevor dies so weit war, wurden Klothoiden auch mit Näherungsformeln berechnet. Dazu ersetzt man die Sinus- und Cosinus-Funktionen in den Fresnel-Integralen durch ihre Potenzreihen, integriert und erhält mit T = L² / 2A² die folgenden Reihenentwicklungen für die x- und y-Werte der Klothoide:

Die Grafik rechts zeigt die mit dieser Reihe (6 Glieder) erzeugte Näherung im Vergleich mit einer "echten" Einheitsklothoide. Durch die Reihenentwicklung im Punkt (0|0) kommt es ab L = 3 zu größeren Abweichungen.
Für den Straßenbau ist dies jedoch nicht weiter tragisch, da dort - bezogen auf die Einheitsklothoide - nur Abschnitte mit L zwischen ungefähr -1.08 und 1.08 in Betracht kommen, d.h. es muss gelten [3], [4]: 3.15° ≤ τ ≤ 28° bzw.
Bei Verwendung einer Näherungslösung für die Klothoide durch eine Reihe reicht es hier vollkommen aus, nur vier Glieder zu verwenden. So beträgt z.B. für A = T = L = 3000 m die Abweichung im Punkt (xL | yL) zur "echten" Klothoide nur ∆x = 0.017 mm sowie ∆y = 0.0008 mm.
Selbst bei nur drei Reihengliedern liegt die Abweichung bei
∆x = 4.9 mm und ∆y = 0.3 mm.
Die Berechnung ist schnell, und es genügt dazu ein Taschenrechner.
Setzt man für die Berechnung von Klothoiden im Straßenbau die alternative Parametrisierung ein, so sollte man N = 106 verwenden, damit z.B. für A = T = L = 3000 m die Abweichungen im Millimeterbereich liegen. Die Rechenzeit auf meiner Kombination aus Hardware und dem Graphing Calculator 3D (s. Tools) beträgt dann 6 Sekunden.
Hier hat mit einer Rechenzeit unter 1 Sekunde die numerische Berechnung der Fresnel-Integrale eindeutig die Nase vorn.
Quellenverweise
[1] https://de.wikipedia.org/wiki/%C3%84hnlichkeit_(Geometrie)
[2] E. Bachmann, Die Klothoide als Übergangskurve im Straßenbau, Schweizerische Zeitschrift für
Vermessung, Kulturtechnik und Photogrammetrie, Band 49 (1951), S. 137 ff,
http://doi.org/10.5169/seals-208340
[3] Bundesministerium für Verkehr, Bau- und Stadtentwicklung, Richtlinien für die
Anlage von Landstraßen
RAL (2012), Kap. 5 Linienführung, S.37
[4] Bundesministerium für Verkehr, Bau- und Stadtentwicklung, Richtlinien für die Anlage von
Autobahnen
RAA (2008), Kap. 5 Linienführung, S.27
[5] M. E. Vázquez-Méndez, G, C. Urcera, The Clothoid Computation: A Simple and Efficient Numerical
Algorithm, Journal of Surveying Engineering, 142(3), (2016),
https://www.researchgate.net/publication/292669884
Download