Die Kardioide (Cardioid)
Die Kardioide oder Herzkurve (von griechisch καρδία
„Herz“) ist eine ebene algebraische Kurve 4. Ordnung, die ihren Namen wegen ihrer Form erhielt. Die ersten Untersuchungen und auch die Namensgebung fanden gegen Ende des 17.
Jahrhunderts statt [1].
Konstruktion der Kardioide
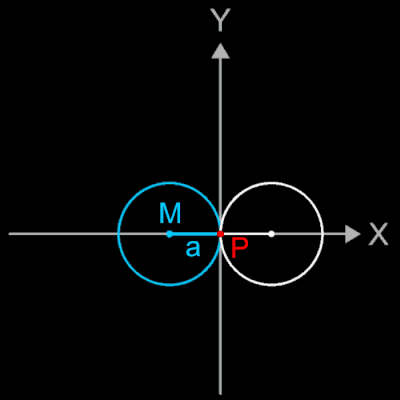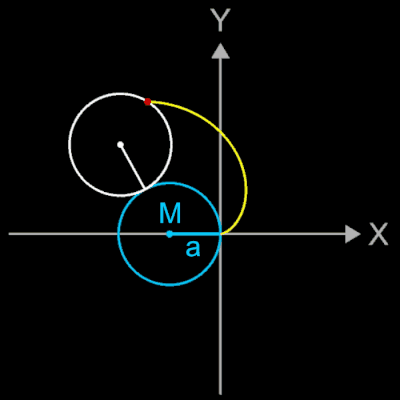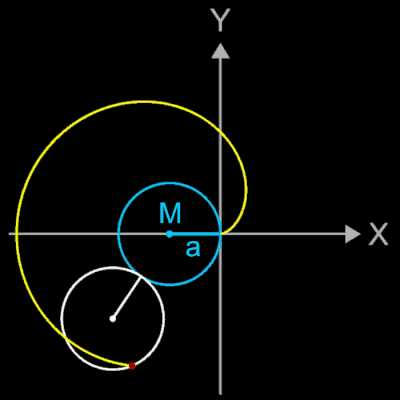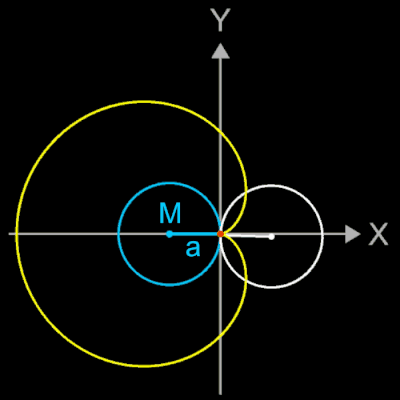
Lässt man auf der Außenseite eines gegebenen festen Kreises mit Mittelpunkt M und Radius a einen weiteren Kreis mit dem gleichen Radius abrollen (s. Animation rechts), und betrachtet man dabei einen bestimmten Punkt P auf dem abrollenden Kreis, so beschreibt P eine spezielle Epizykloide, die Kardioide (––––).
Ist a der gemeinsame Radius der erzeugenden Kreise mit den Mittelpunkten (-a | 0) und (a | 0), φ der Rollwinkel und der Nullpunkt der Startpunkt (s. Bild), so erhält man die
Parameterdarstellung:
x ( φ ) = 2 a ( 1 − cos (φ) ) ⋅ cos (φ) ,
y ( φ ) = 2 a ( 1 − cos (φ) ) ⋅ sin (φ) , 0 ≤ φ < 2 π
Hieraus ergibt sich die Darstellung in Polarkoordinaten:
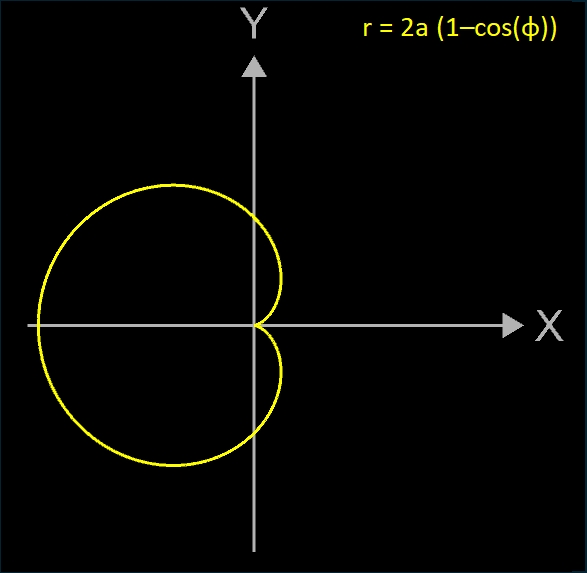
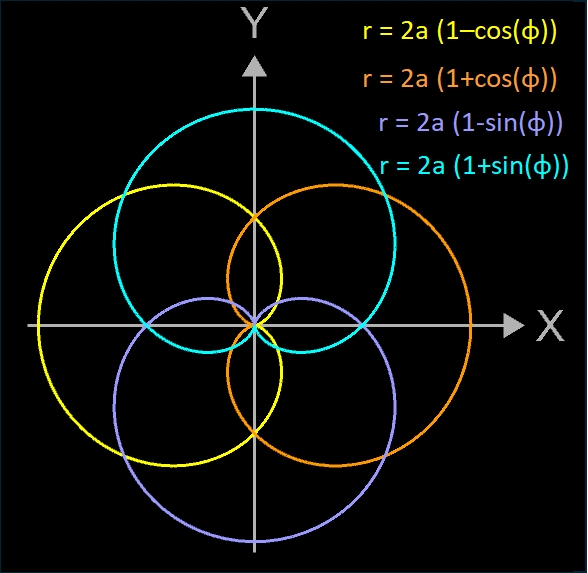
r ( φ ) = 2 a ( 1 − cos (φ) )
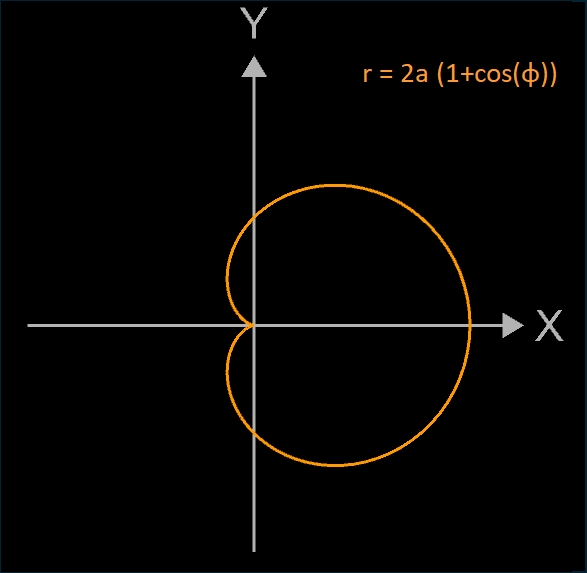
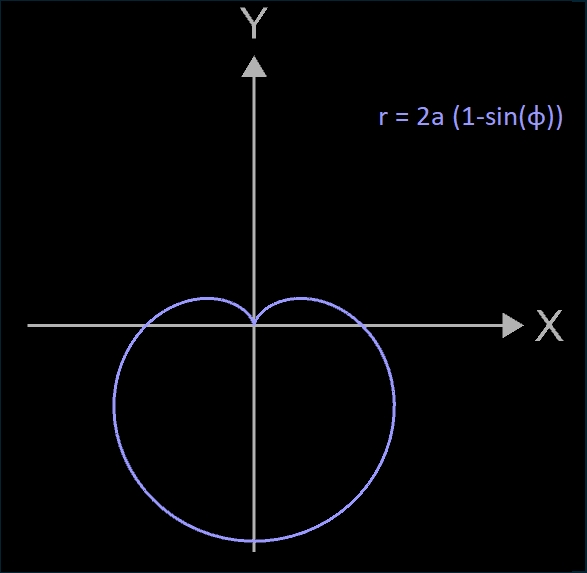
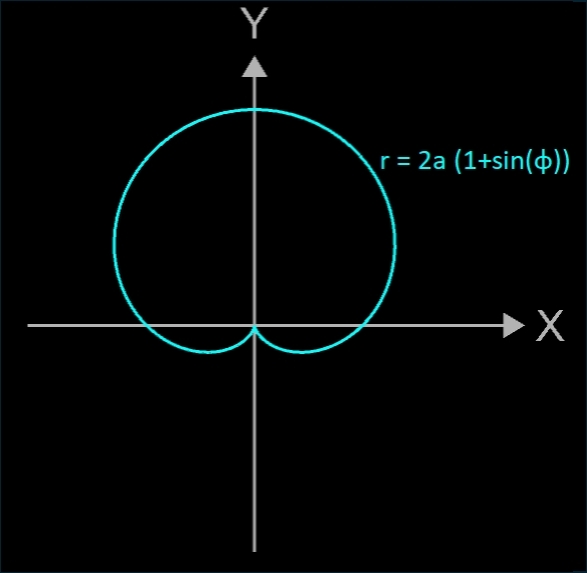
Durch Anpassen der Funktionsgleichungen lassen sich 4 Lagen der Kardioide erzeugen (s. Galerie rechts).
Die Berechnung der Länge L des Funktionsgraphen sowie der Fläche A unter der Kurve bestimmt man mit Hilfe der Integralrechnung: