Fläche unter parametrischer Funktion
Ist die Funktion in parametrischer Form gegeben durch
x = fx (t) , y = fy (t) , so beträgt die Fläche A unter f
und fx (ta) = a und fy (tb) = b für ta ≤ t ≤ tb.
Fläche unter Ellipse
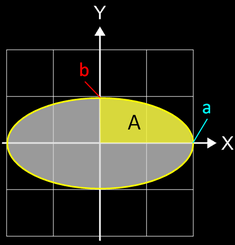
Die Fläche einer Ellipse mit x = fx (t) = a cos (t) und y = fy (t) = b sin (t) soll bestimmt werden.
Die Fläche besteht aus 4 Teilflächen, die alle gleich groß wie A im Intervall [0, a] sind. Für A gilt x = 0 →
ta =
π
/ 2 , x = a
→
tb = 0
und
fx ' (t) = - a sin(t).
Die entsprechende Datei für den Graphing Calculator 3D (s. unten im Download-Bereich) liefert z.B. für a = 2 und b =1 das Ergebnis mit einer Genauigkeit von 14 Nachkommastellen:
Fläche unter Zykloide
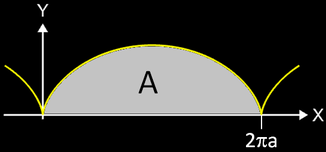
Für eine Zykloide mit der parametrischen Funktion
x = fx (t) = a ( t - sin (t) ) und y = fy (t) = a ( 1 - cos (t) )
soll die Fläche A im Intervall [0, 2π] bestimmt werden
(diese wurde auch zur Berechnung des Volumens eines American Football, s. Volumen mit parametrischer Funktion verwendet).
Es gilt: x = 0 → ta = 0 x = 2 π a → tb = 2 π und fx ' (t) = a ( 1 - sin (t) ).
Für z.B. a = 1 liefert Graphing Calculator 3D das Ergebnis mit einer Genauigkeit von 13 Nachkommastellen.
Fläche unter Archimedischer Spirale
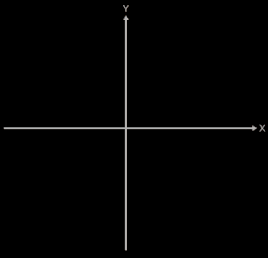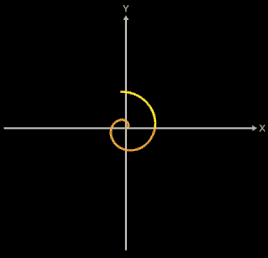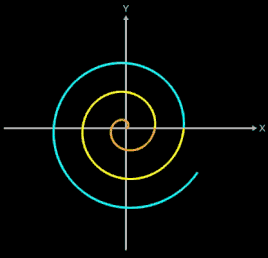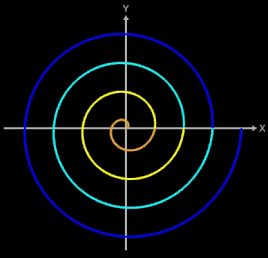
Es soll die Fläche unter einer Archimedischen Spirale bestimmt werden.
Diese entsteht, wenn - ausgehend von einem Kreis mit
x = r
• cos (φ)
und y
=
φ
• sin (φ)
- der Radius r proportional zum Drehwinkel φ
zunimmt: r = a • φ
mit a>0. Somit wird sie erzeugt mit der parametrischen Funktion
x = fx (t) = a • φ • cos (φ) und y = fy (φ) = a • φ • sin (φ).
Für eine erste Umdrehung (n = 1) mit
φ = 0 ... 2
π gilt:
φ = 0 → φa = 0 φ = 2 π → φb = 2 π
fx ' (φ) = a ( cos (φ) - φ sin (φ)
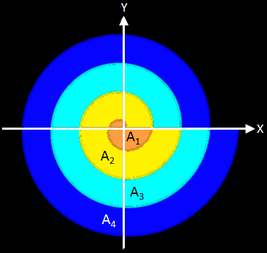
Für weitere Umdrehungen ergibt sich für die Gesamte Fläche unter der Spirale folgendes Schema:
n = 2:
n = 3:
n = 4:
und schließlich allgemein für n Umdrehungen:
Download

