Fläche unter Funktion in Polarkoordinaten
Flächen werden auf Grund ihrer Anwendung oft auch in Polarkoordinaten [1] dargestellt; in der Regel vereinfacht sich der Funktionsterm dabei deutlich.
Ist r = f (φ) die Kurve einer Funktion in Polarkoordinaten, dann gilt für die Fläche A unter der Kurve und zwischen den beiden Radiusvektoren φ0 und φ1 ( φ0 < φ1 ) [2]:
Fläche der Kardioide in Polarkoordinaten
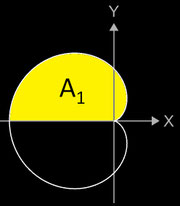
Bei der Berechnung der Kardioide mit der Gleichung r = f (φ)
= a •
(1-cos(φ)
kann man die Symmetrie zur x-Achse ausnutzen:
Archimedische Spirale in Polarkoordinaten
Die Gleichung einer Archimedischen Spirale in Polarkoordinaten lautet r = f (φ) = a • φ.
Für den Bereich von
φ = 0 ...
2π
(erste vollständige Umdrehung) ergibt sich für die Fläche:
Die Berechnung des Integrals ist ein Kinderspiel im Vergleich zum Integral, das sich ergibt, wenn die Archimedische Spirale durch eine parametrische Funktion in kartesischen Koordinaten erzeugt wird (vgl. Archimedische Spirale unter Fläche unter parametrischer Funktion).
Die Flächenberechnung nach obiger Gleichung ist nur dann korrekt, falls
φ1 -
φ0 ≤
2π
gilt!
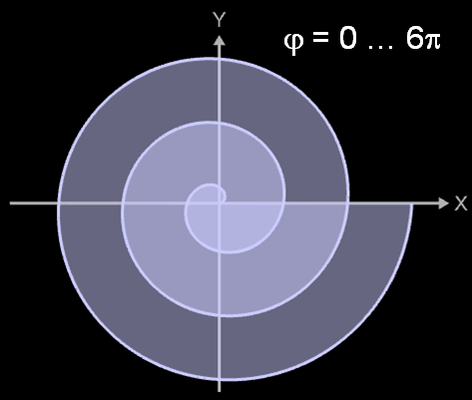
Soll z.B. die Fläche nach 3 Umdrehungen, also für φ = 0 ... 6π, bestimmt werden, so ist zu beachten, dass Winkelbereiche mehrfach "überstrichen" werden, was in der folgenden Bildsequenz zu erkennen ist.
Hier wird die Fläche unter der Spirale stets mit dem gleichen Farbton (hellgrau) gefüllt. Dadurch, dass innenliegende Bereiche mehrfach überstrichen werden (Bereich φ = 0 ... 2π dreimal, φ = 2π ... 4π zweimal), sind diese Bereiche heller:
Für die Fläche nach 3 vollständigen Umdrehungen ergibt sich A demnach nicht (!) einfach zu
Dieser Wert ist wegen der mehrfachen Überstreichungen von
φ deutlich zu groß. Vielmehr sind
φ0 und
φ1 entsprechend anzupassen, so dass sich als korrekte Lösung für die Fläche A (s. Grafik) ergibt:

Dies macht Polarkoordinaten so "tricky" ... ;-)
Zum Vergleich wird hier noch die Fläche mit der Summenformel für die Archimedische Spirale berechnet (s. Archimedische Spirale unter Fläche unter parametrischer Funktion):
Mit n = 3 ergibt sich:

Die Datei im Download-Bereich für den Graphing Calculator 3D berechnet die Fläche unter einer Archimedischen Spirale zwischen
φ0 = 0 und beliebigem
φ1 und stellt die bei der Flächenberechnung zu berücksichtigenden Bereiche für
φ grafisch dar.
Die Grafik zeigt eine Animation für φ1 = 0 ... 3π.
Quellenverweise
[1] https://de.wikipedia.org/wiki/Polarkoordinaten
[2] Sharma, A. K. (2005), Application Of Integral Calculus, Discovery Publishing House, S. 4 - 5
Download