Phase Plots komplexer Funktionen - Galerie 3

 

Auf dieser Seite finden Sie Phasen-Plots (Phasen-Porträts) für eine Vielzahl komplexer Funktionen f  mit dem Definitionsbereich D ⊂ ℂ und Wertebereich W ⊂ ℂ   

f : B ⊂ D ⊆ ℂ → W ⊆ ℂ : z ↦ w

Falls nicht anders angegeben, gilt für den dargestellten Bereich
B = [-3, 3] x [-3, 3].

 

Die Funktionen sind nach ihrem Typ sortiert; durch Anklicken eines Typs im Kasten springen Sie direkt zu diesem. Weitere Funktionstypen finden Sie in Galerie 1 und Galerie 2.

 

Um die Ladezeiten kurz zu halten, wurden die JPG-Grafiken mit einer Auflösung von 1024 x 1024 Pixel bei 95% Qualität gespeichert.

 

Interessierte Leser(innen) können für eigene Darstellungen und Experimente auf einen Shader und weitere Informationen im Download-Bereich unten auf der Seite zugreifen.

Funktionstypen
  • Polynome
  • Rationale Funktionen
  • Exponentialfunktionen
  • Wurzelfunktionen
  • Trigonometr. Funktionen
  • Arcus-Funktionen
  • Hyperbolische Funktionen
  • Area-Funktionen

Klicken Sie auf ein Bild für eine vergrößerte Ansicht und Anzeige von Einfärbe-Modell (Typ) und Bereich B. Für eine weitere Vergrößerung klicken Sie auf die Bildschirmlupe , mit den  Pfeiltasten ←  → am linken / rechten Bildschirmrand bewegen Sie sich innerhalb der Galerie.


•  Gemischte Funktionstypen

  • Phase Plot, Funktion 23, Typ=0, B=[-8, 4]x[-6, 6]
  • Phase Plot, Funktion 23, Typ=1, B=[-8, 4]x[-6, 6]
  • Phase Plot, Funktion 23, Typ=2, B=[-8, 4]x[-6, 6]
  • Phase Plot, Funktion 23, Typ=4, B=[-8, 4]x[-6, 6]

  • Phase Plot, f(z)=exp(z) sin(z), Typ=0, B=[-4, 4]x[-4, 4]
  • Phase Plot, f(z)=exp(z) sin(z), Typ=4, B=[-4, 4]x[-4, 4]

  • Phase Plot, Funktion 30, Typ=0, B=[-2, 2]x[-2, 2]
  • Phase Plot, Funktion 30, Typ=1, B=[-2, 2]x[-2, 2]
  • Phase Plot, Funktion 30, Typ=2, B=[-2, 2]x[-2, 2]
  • Phase Plot, Funktion 30, Typ=0, B=[-1.1, 1.1]x[-1.1, 1.1]

  • Phase Plot, f(z)=asec(z)(z²-cos(z)), Typ=0, B=[-2, 2]x[-2, 2]
  • Phase Plot, f(z)=asec(z)(z²-cos(z)), Typ=1, B=[-2, 2]x[-2, 2]
  • Phase Plot, f(z)=asec(z)(z²-cos(z)), Typ=2, B=[-2, 2]x[-2, 2]
  • Phase Plot, f(z)=asec(z)(z²-cos(z)), Typ=4, B=[-2, 2]x[-2, 2]
  • Phase Plot, f(z)=asec(z)(z²-cos(z)), Typ=6, B=[-2, 2]x[-2, 2]

  • Phase Plot, f(z)=Re(z+1)²)+i•Re((z-1)²), Typ=0, B=[-5, 5]x[-5, 5]
  • Phase Plot, f(z)=Re(z+1)²)+i•Re((z-1)²), Typ=1, B=[-5, 5]x[-5, 5]
  • Phase Plot, f(z)=Re(z+1)²)+i•Re((z-1)²), Typ=2, B=[-5, 5]x[-5, 5]
  • Phase Plot, f(z)=Re(z+1)²)+i•Re((z-1)²), Typ=4, B=[-5, 5]x[-5, 5]
  • Phase Plot, f(z)=Re(z+1)²)+i•Re((z-1)²), Typ=6, d=2, B=[-5, 5]x[-5, 5]

Mandelbrot-Menge

  • Mandelbrot-Menge k=3
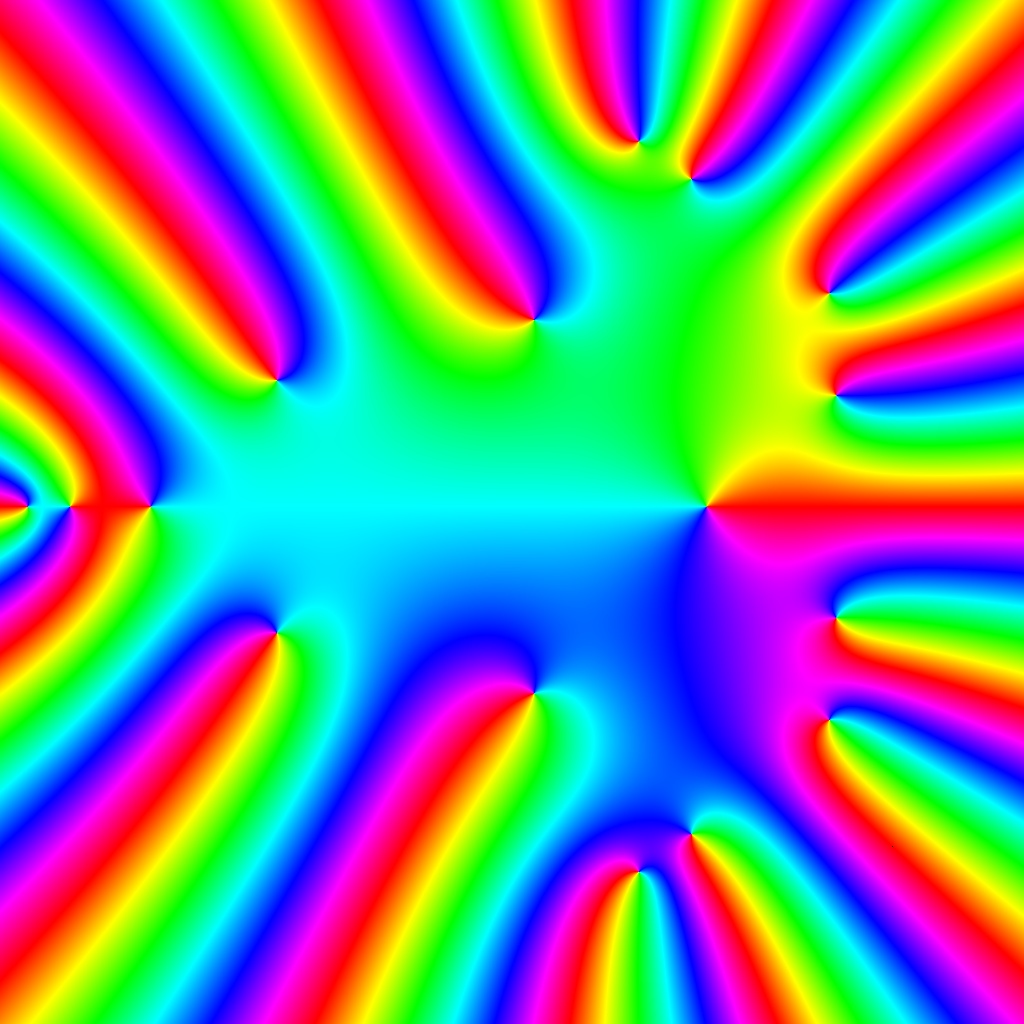
  • Mandelbrot-Menge k=5
  • Mandelbrot-Menge k=7
  • Mandelbrot-Menge k=9
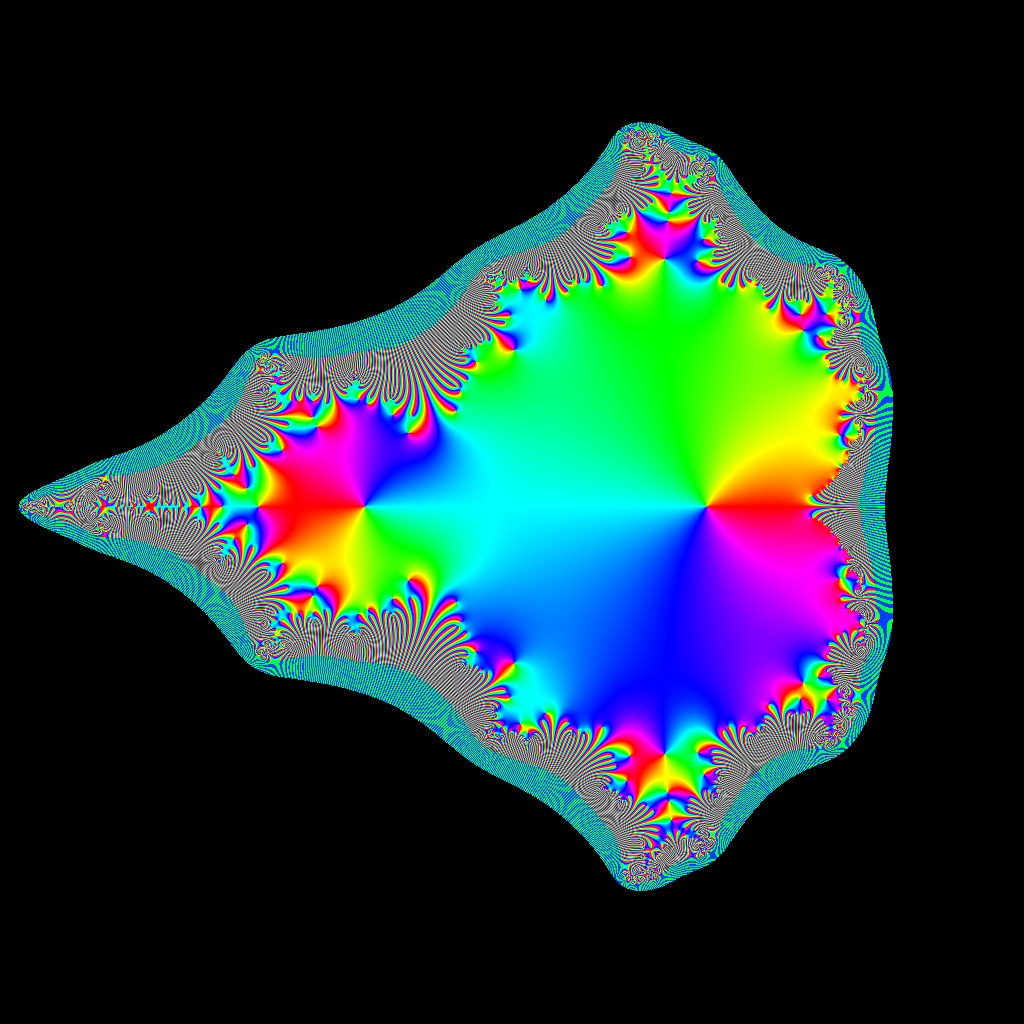
  • Mandelbrot-Menge k=12
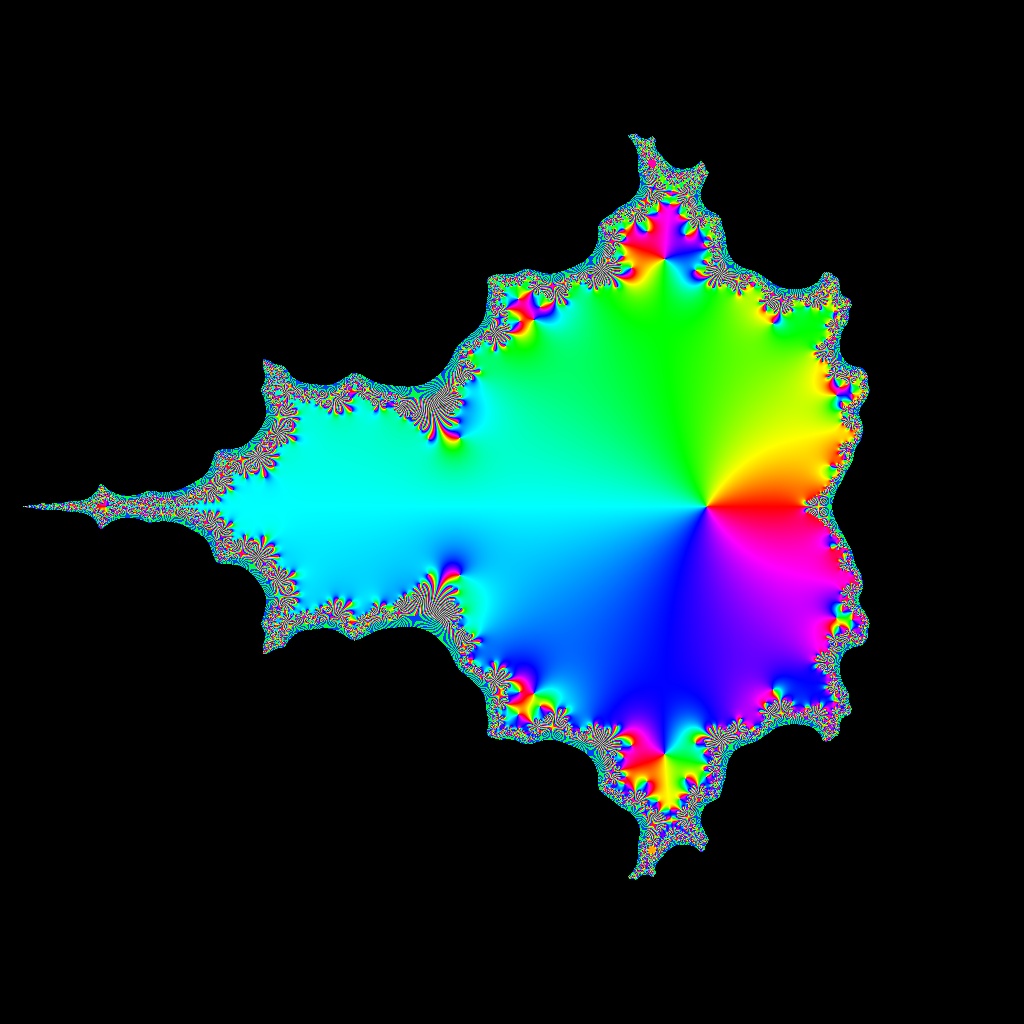
  • Mandelbrot-Menge k=15
  • Mandelbrot-Menge k=20
  • Mandelbrot-Menge k=204

Julia-Menge

  • Julia-Menge c=-0.1-0.66 i, k=8
  • Julia-Menge c=-0.1-0.66 i, k=20
  • Julia-Menge c=0.7 i, k=20
  • Julia-Menge c=0.37+0.1 i, k=20
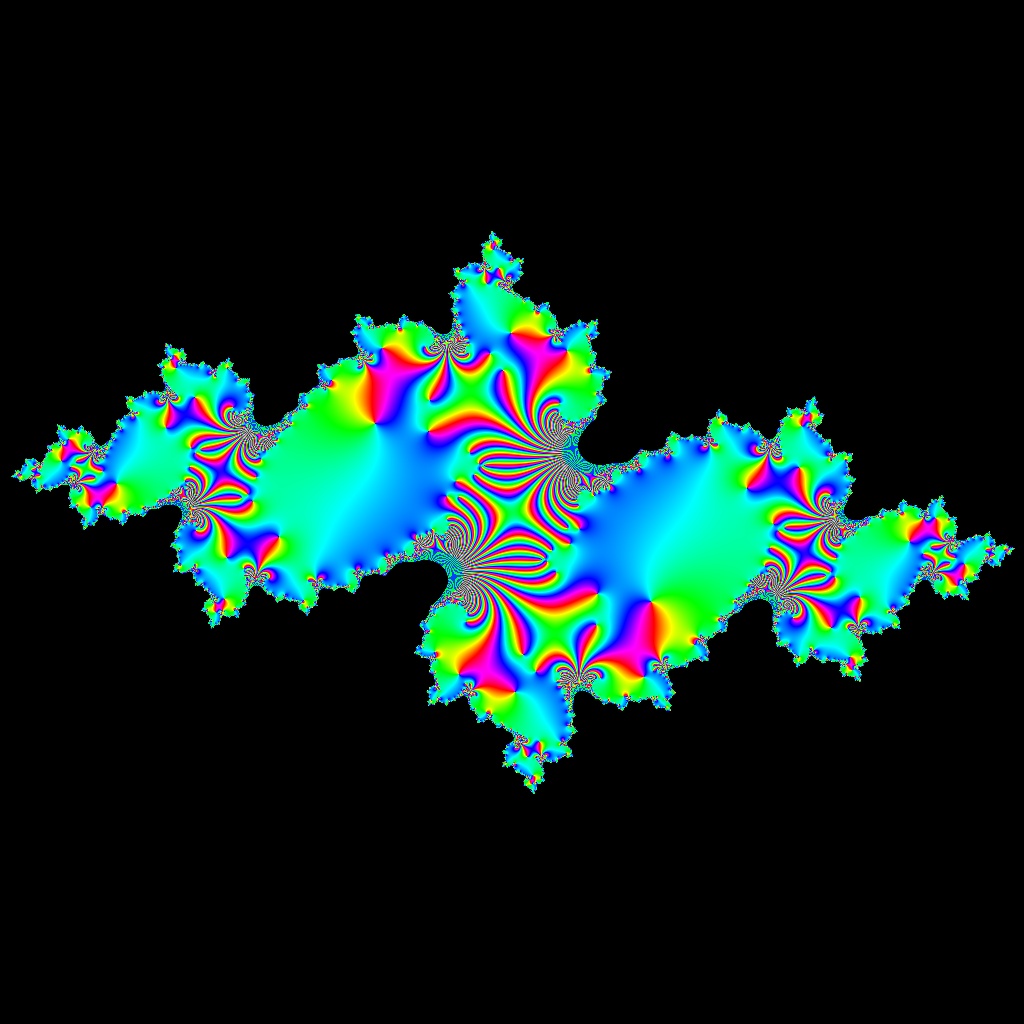
  • Julia-Menge c=-0.75,+0.22 i, k=20
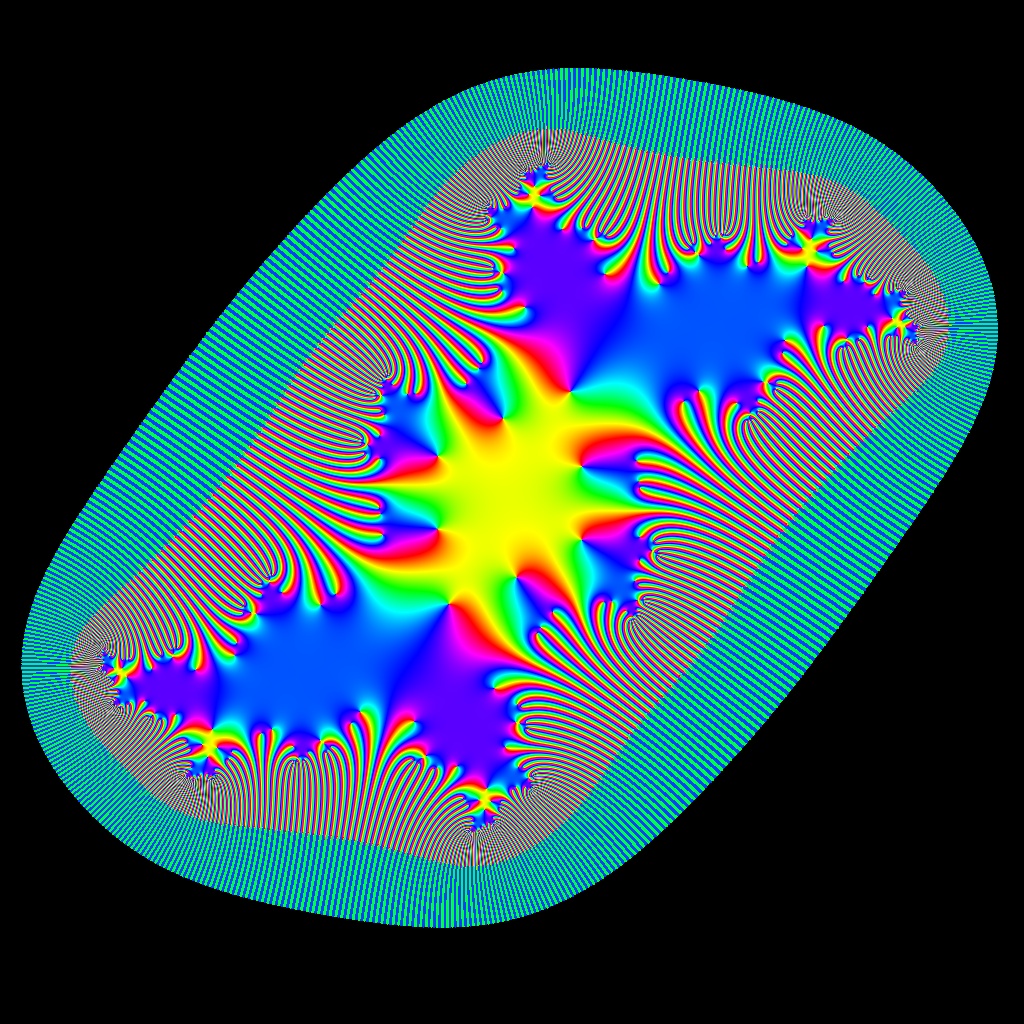
  • Julia-Menge c=-0.117-0.779 i, k=10
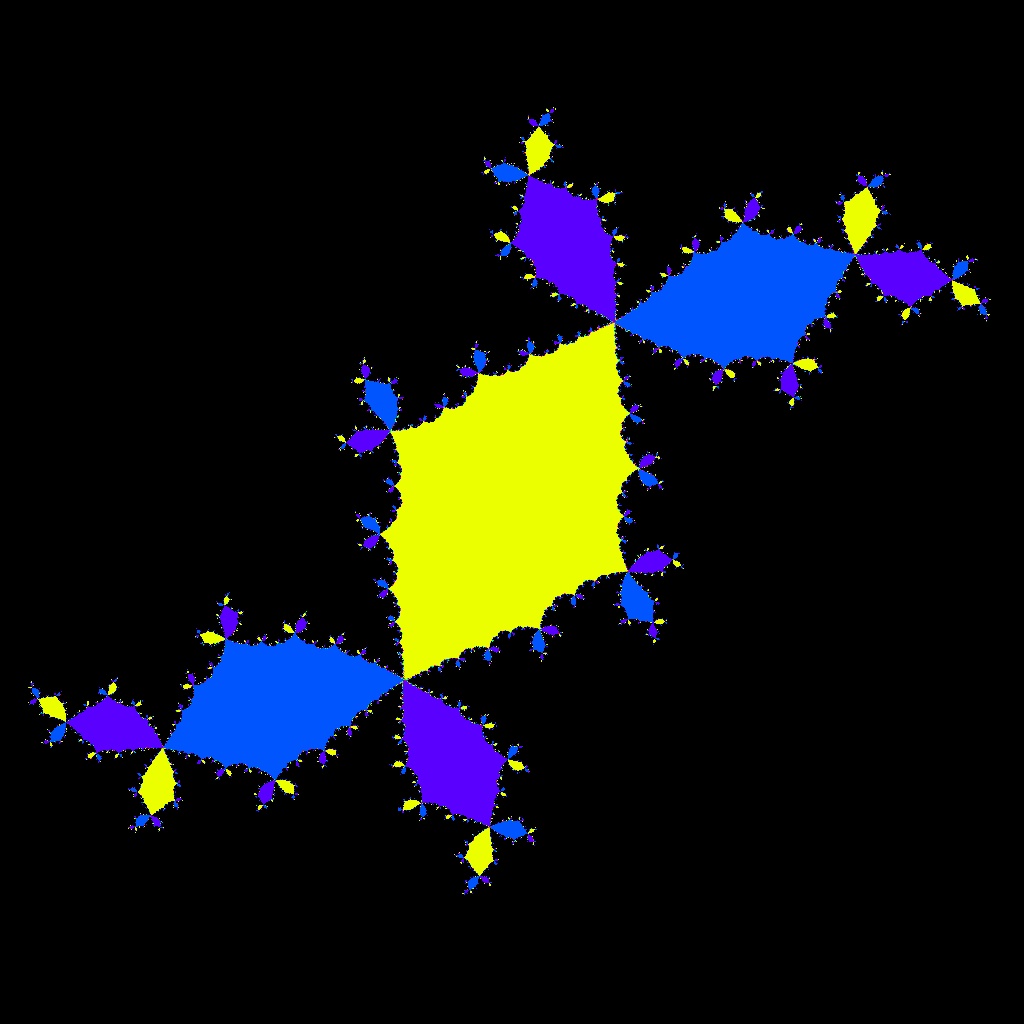
  • Julia-Menge c=-0.117-0.779 i, k=40
  • Julia-Menge c=-1, k=8
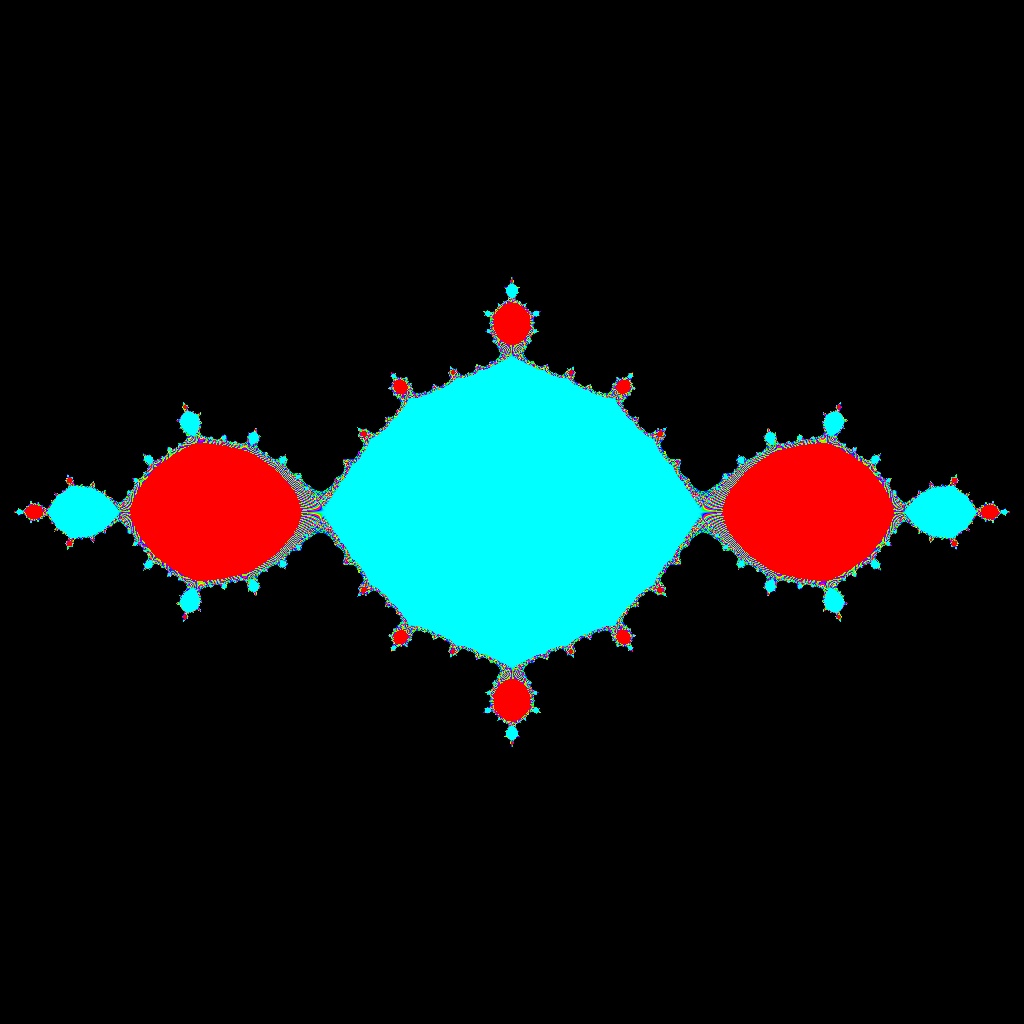
  • Julia-Menge c=-1, k=20

Newton-Verfahren für z3 – 1 = 0, 

s. auch hier

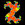
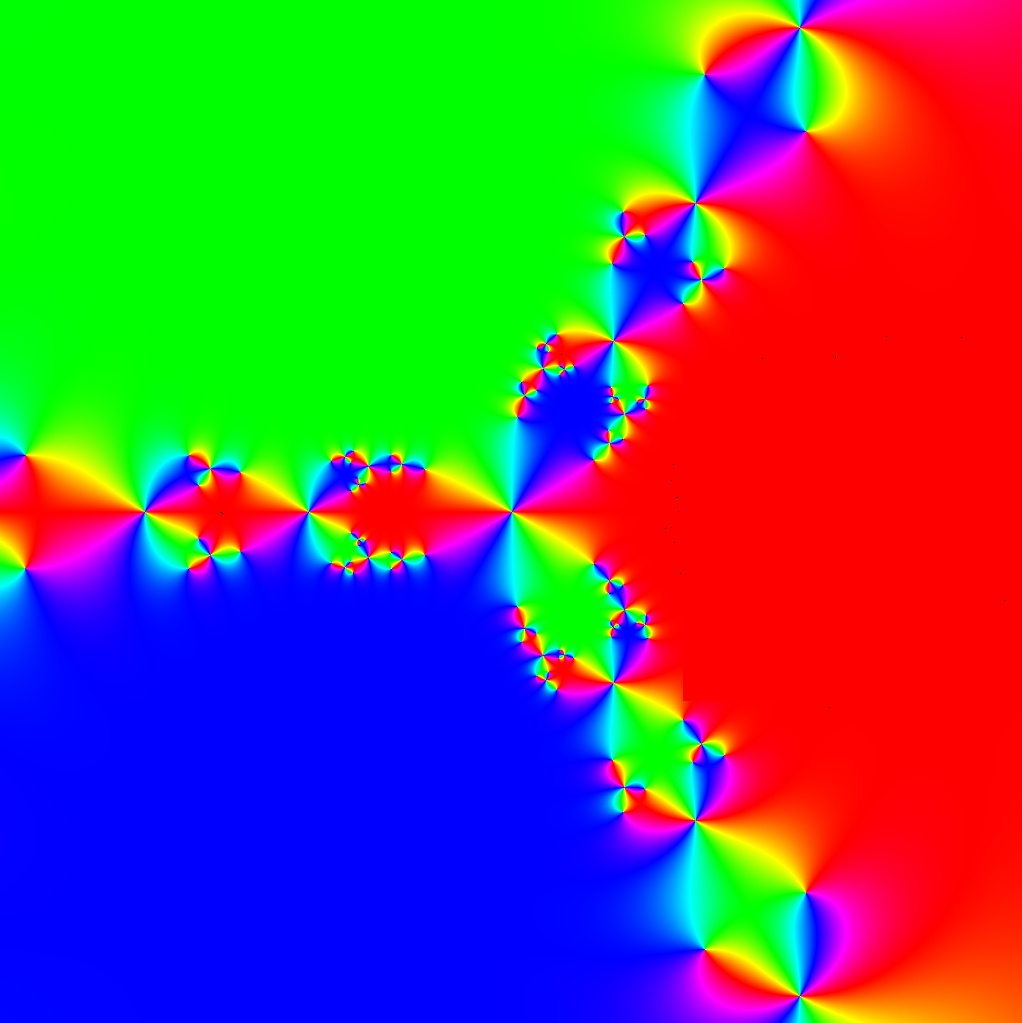
  • Newton-Verfahren z<sup>3</sup>-1=0, k=4, Typ=0
  • Newton-Verfahren z<sup>3</sup>-1=0, k=4, Typ=1
  • Newton-Verfahren z<sup>3</sup>-1=0, k=4, Typ=2

Newton-Verfahren für z3 – 1 = 0,

  • Newton-Verfahren z<sup>3</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>1</sub>, Typ=0
  • Newton-Verfahren z<sup>3</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>2</sub>, Typ=0
  • Newton-Verfahren z<sup>3</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>3</sub>, Typ=0

Newton-Verfahren für z4 – 1 = 0,
s. auch hier

  • Newton-Verfahren z<sup>4</sup>-1=0, k=4, Typ=0
  • Newton-Verfahren z<sup>4</sup>-1=0, k=4, Typ=1
  • Newton-Verfahren z<sup>4</sup>-1=0, k=4, Typ=2

Newton-Verfahren für z4 – 1 = 0

  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>1</sub>, Typ=0
  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>2</sub>, Typ=0
  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>3</sub>, Typ=0
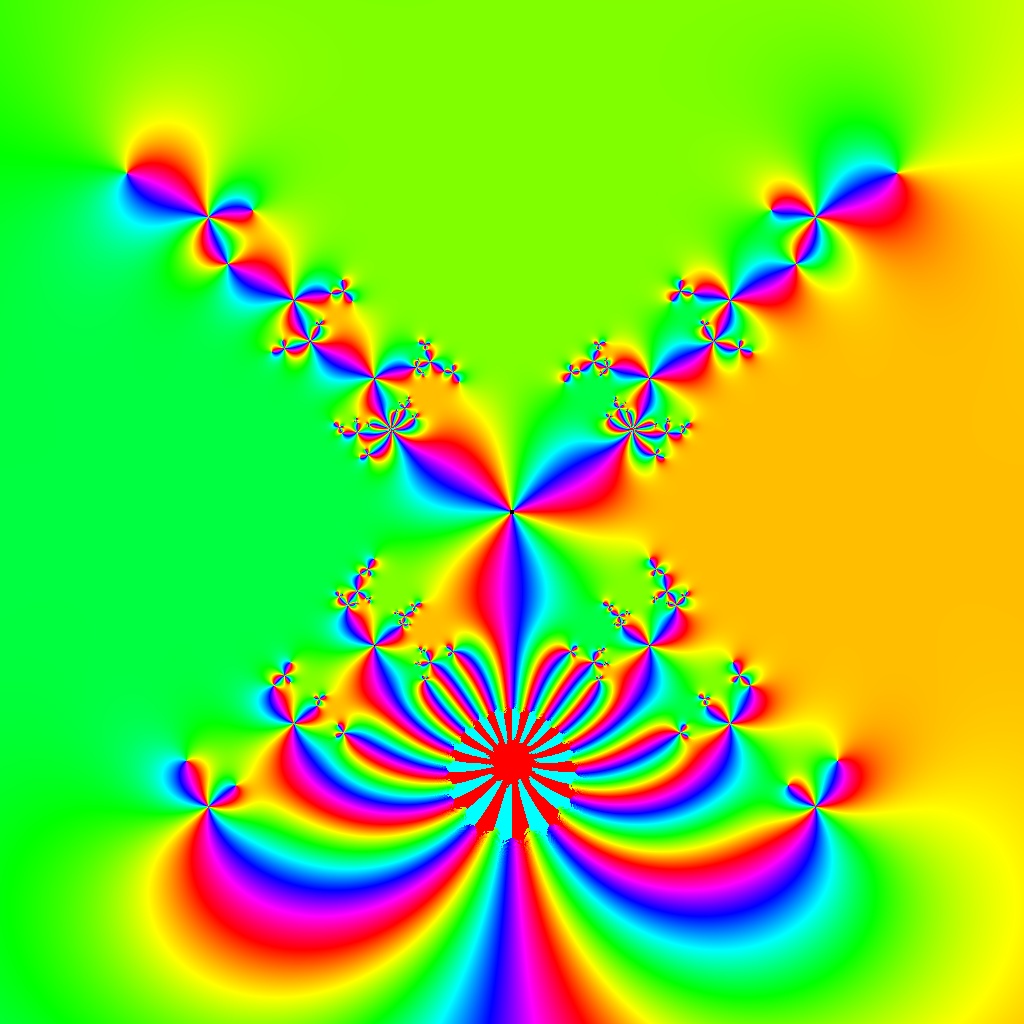
  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>4</sub>, Typ=0
  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>1</sub>, Typ=1
  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>2</sub>, Typ=1
  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>3</sub>, Typ=Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>3</sub>, Typ=1
  • Newton-Verfahren z<sup>4</sup>-1=0, Residuen f<sub>4</sub>(z)-ξ<sub>4</sub>, Typ=1

  • f(z)=ln(cos(z<sup>5</sup>-z<sup>-5</sup>))
  • f(z)=ln(cos(z<sup>5</sup>-z<sup>-5</sup>)), Zoom a
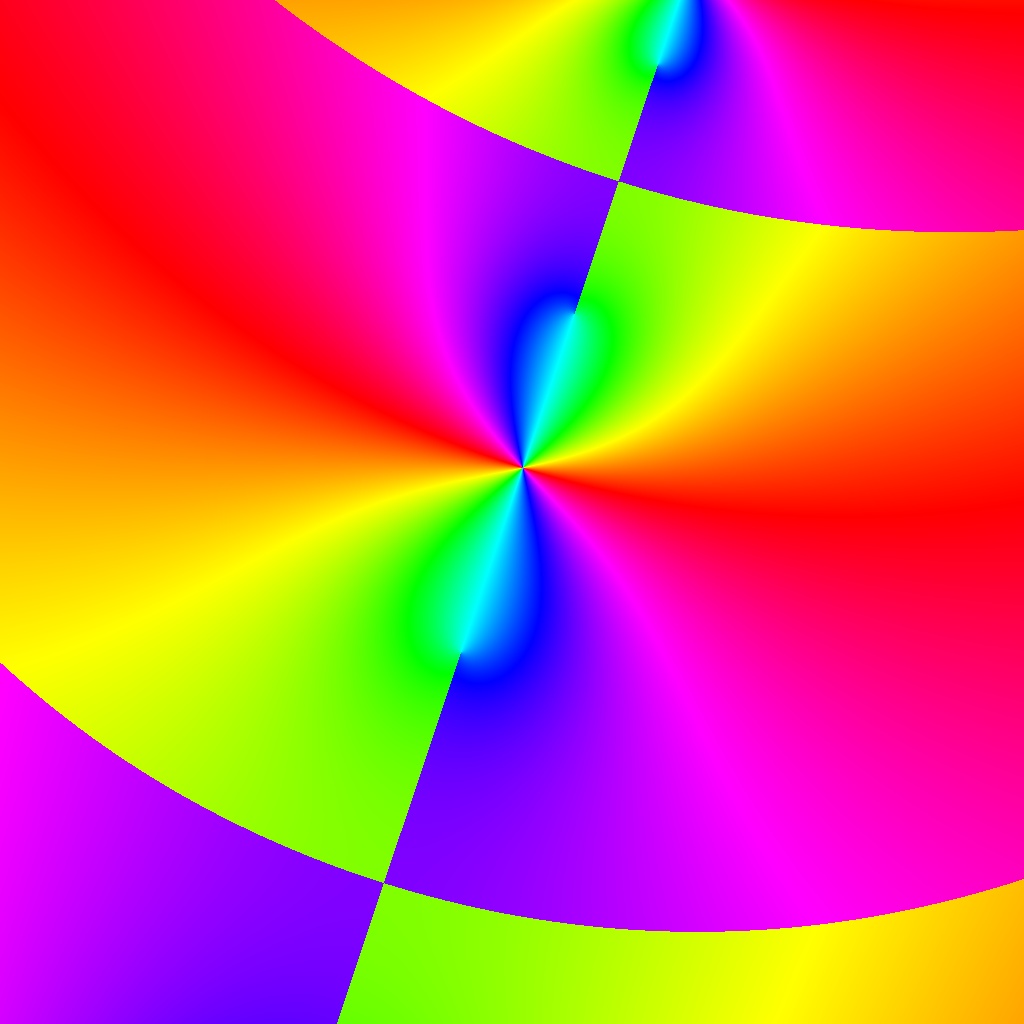
  • f(z)=ln(cos(z<sup>5</sup>-z<sup>-5</sup>)), Zoom b

Finites Blaschke-Produkt

  • Blaschke-Produkt, m1,..,m12=1, zeta=1
  • Blaschke-Produkt, m1,..,m12=2, zeta=1
  • Blaschke-Produkt, m1,..,m12=1, zeta=random
  • Blaschke-Produkt, m1,..,m12=2, zeta=random

Finites Blaschke-Produkt

  • Blaschke-Produkt m=1, zeta=random, r=5, nmax=50, B=[-4, 4]x[-4,4]
  • Blaschke-Produkt m=3, zeta=random, r=3, nmax=100, B=[-4, 4]x[-4,4]
  • Blaschke-Produkt m=3, zeta=random, r=4, nmax=5, B=[-4, 4]x[-4,4]
  • Blaschke-Produkt m=3, zeta=random, r=4, nmax=7, B=[-2, 2]x[-3, 1]
  • Blaschke-Produkt m=4, zeta=random, r=5, nmax=50, B=[-10, 10]x[-10,10]
  • Blaschke-Produkt m=1, zeta=random, r=3, nmax=200, B=[-10, 10]x[-10,10]


•  Reihen

vgl. auch mit Komplexe Folgen und Reihen

  • Phase Plot f(z)=nsum z^n, n=10, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=0
  • Phase Plot f(z)=nsum z^n, n=100, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=0
  • Phase Plot f(z)=nsum z^n, n=100, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=1
  • Phase Plot f(z)=nsum z^n, n=100, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=2

vgl. auch mit Komplexe Folgen und Reihen

  • Phase Plot f(z)=nsum nz^n, n=10, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=0
  • Phase Plot f(z)=nsum nz^n, n=100, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=0
  • Phase Plot f(z)=nsum nz^n, n=10, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=1
  • Phase Plot f(z)=nsum nz^n, n=10, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=2
  • Phase Plot f(z)=nsum nz^n, n=10, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=4

  • Phase Plot f(z)=nsum n^2 z^n, n=10, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=0
  • Phase Plot f(z)=nsum n^2 z^n, n=100, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=0
  • Phase Plot f(z)=nsum n^2 z^n, n=100, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=1
  • Phase Plot f(z)=nsum n^2 z^n, n=100, B=[-1.2, 1.2]x[-1.2, 1.2], Typ=4

 

vgl. auch mit Komplexe Folgen und Reihen

 

  • Phase Plot f(z)=nsum 1 div z^n, n=10, B=[-1.5, 1.5]x[-1.5, 1.5], Typ=0
  • Phase Plot f(z)=nsum 1 div z^n, n=100, B=[-1.5, 1.5]x[-1.5, 1.5], Typ=0
  • Phase Plot f(z)=nsum 1 div z^n, n=100, B=[-1.5, 1.5]x[-1.5, 1.5], Typ=1
  • Phase Plot f(z)=nsum 1 div z^n, n=100, B=[-1.5, 1.5]x[-1.5, 1.5], Typ=2

vgl. auch mit Komplexe Folgen und Reihen

  • Phase Plot f(z)=nsum of (z div z+1)^n, nmax=40, Typ=0
  • Phase Plot f(z)=nsum of (z div z+1)^n, nmax=40, Typ=1
  • Phase Plot f(z)=nsum of (z div z+1)^n, nmax=40, Typ=2
  • Phase Plot f(z)=nsum of (z div z+1)^n, nmax=40, Typ=4

    

vgl. auch mit Komplexe Folgen und Reihen

  • Phase Plot f(z)=nsum z^n, nmax=5, Typ=0
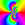
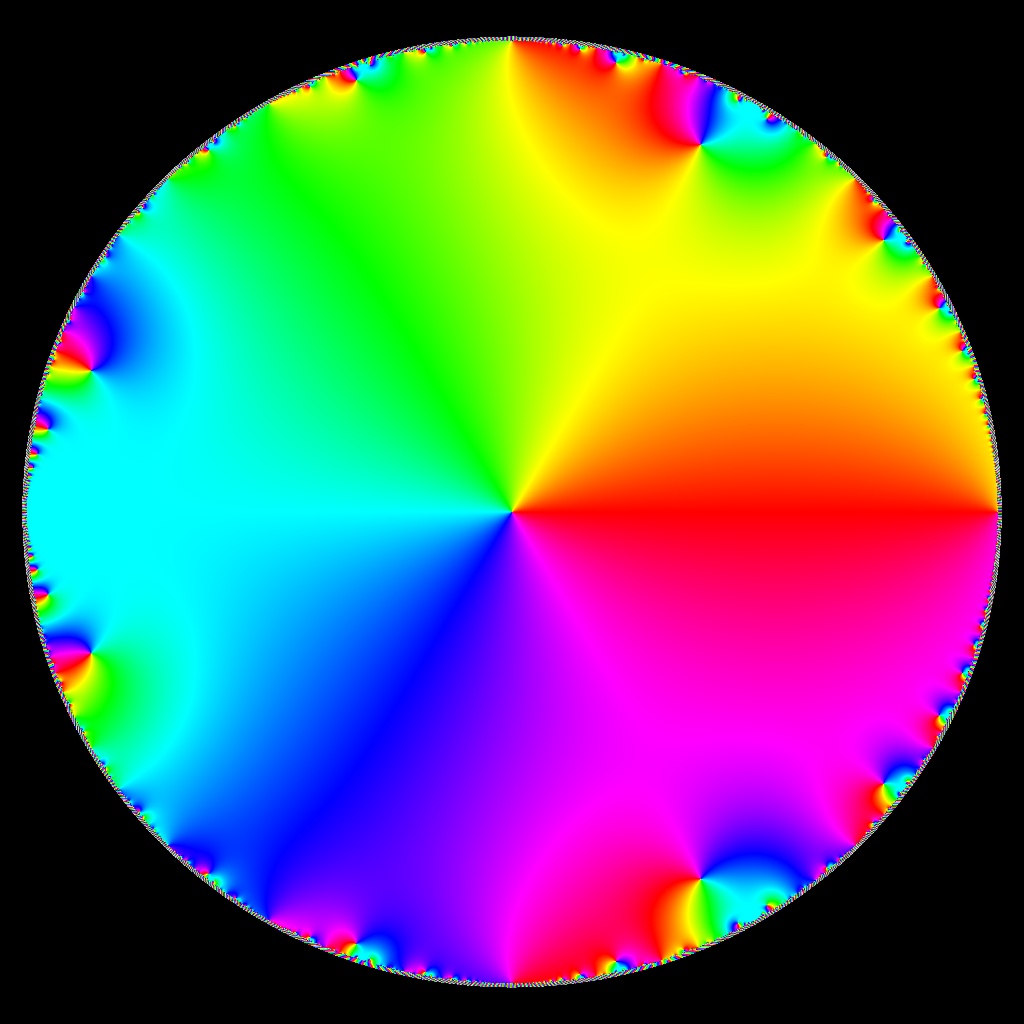
  • Phase Plot f(z)=nsum z^n, nmax=100, Typ=0
  • Phase Plot f(z)=nsum z^n, nmax=100, Typ=1
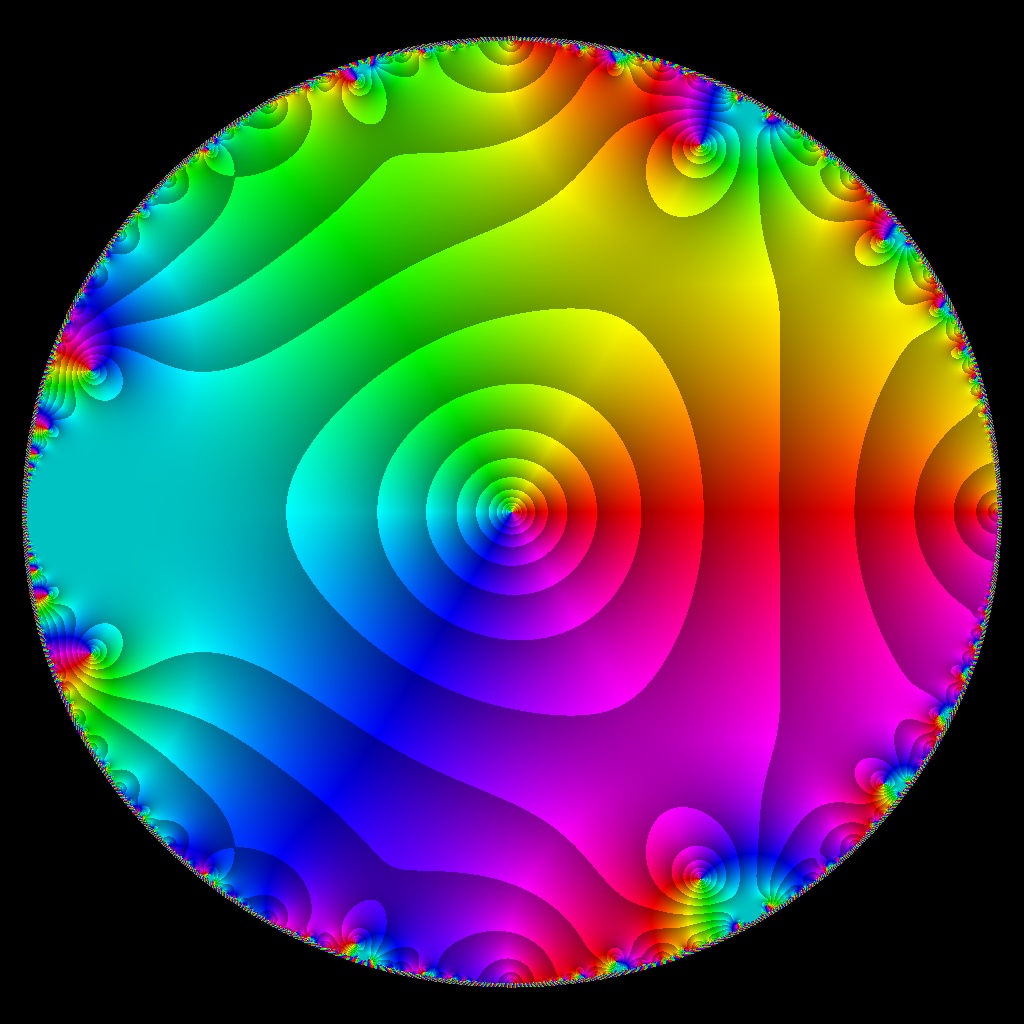
  • Phase Plot f(z)=nsum z^n, nmax=100, Typ=2

 

vgl. auch mit Komplexe Folgen und Reihen

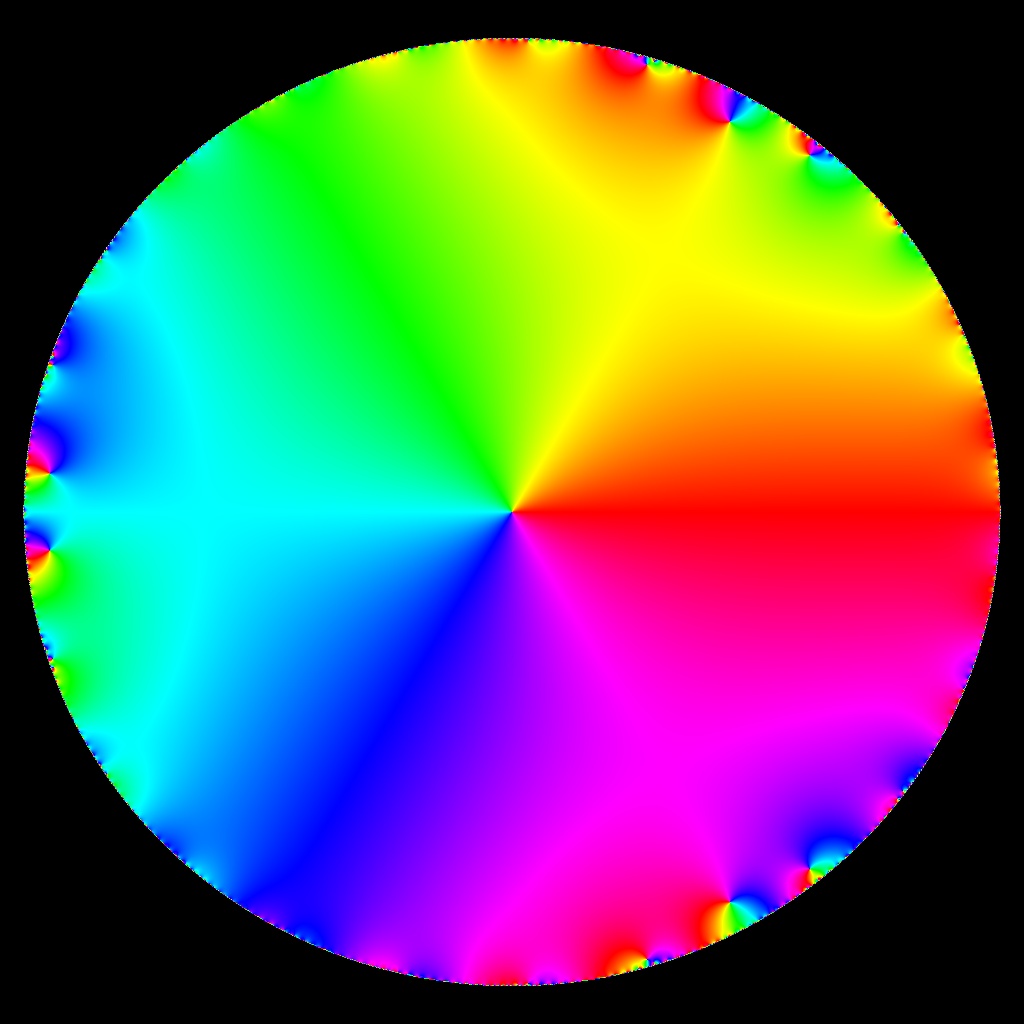
  • Phase Plot f(z)=nsum z^n!, nmax=8, Typ=0
  • Phase Plot f(z)=nsum z^n!, nmax=8, Typ=1
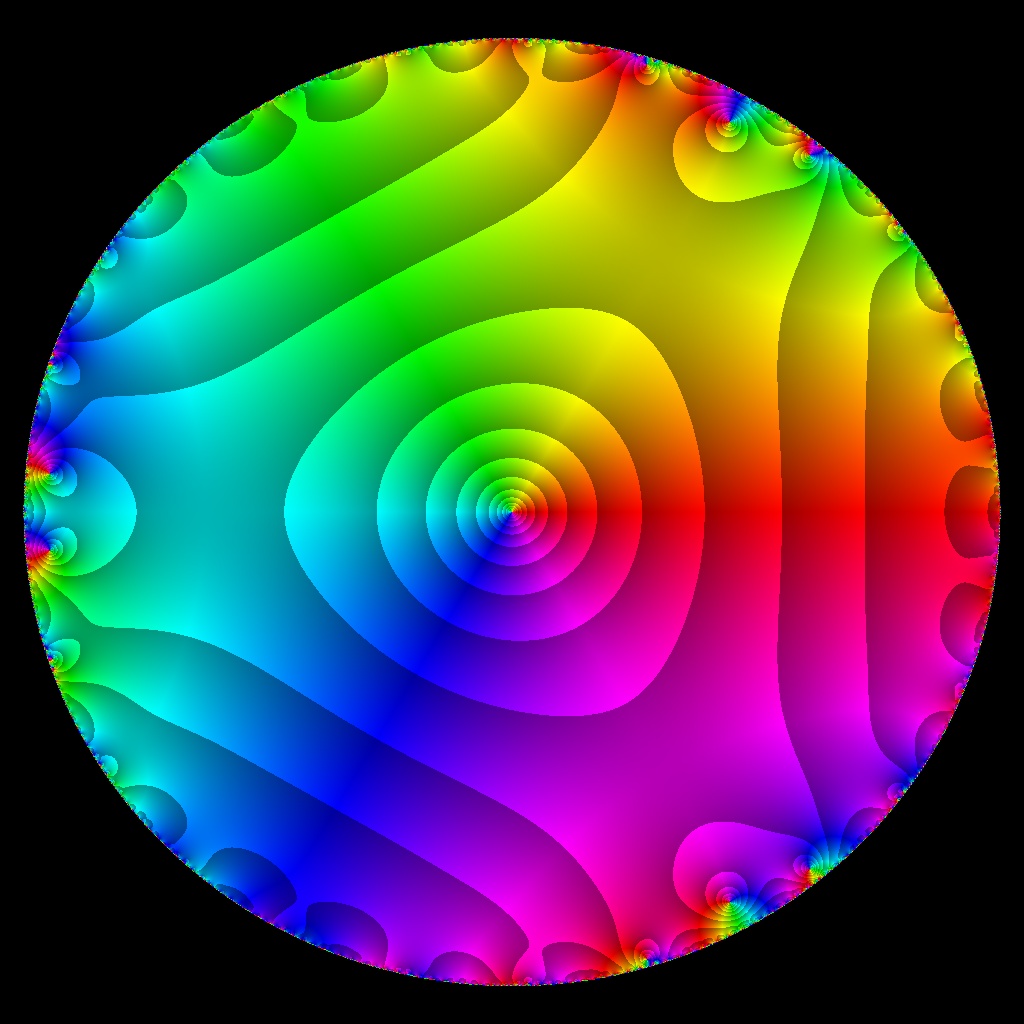
  • Phase Plot f(z)=nsum z^n!, nmax=8, Typ=2

  • Phase Plot f(z)=nsum (1 div 2z+1) z^(2n+1), nmax=50, Typ=0
  • Phase Plot f(z)=nsum (1 div 2z+1) z^(2n+1), nmax=50, Typ=1
  • Phase Plot f(z)=nsum (1 div 2z+1) z^(2n+1), nmax=50, Typ=2
  • Phase Plot f(z)=nsum (1 div 2z+1) z^(2n+1), nmax=50, Typ=4

  • Phase Plot, f(z)=ksum z^k•i, kmax=3, Typ=0, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=3, Typ=1, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=3, Typ=2, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=3, Typ=4, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=3, Typ=6, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=12, Typ=0, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=12, Typ=1, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=12, Typ=2, B=[-15, 15]x[-15, 15]
  • Phase Plot, f(z)=ksum z^k•i, kmax=12, Typ=4, B=[-15, 15]x[-15, 15]

Polygamma-Funktion

  • Phase Plot, Polygamma-Funktion, m=0, K=50, Typ=1, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=0, K=50, Typ=4, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=0, K=50, Typ=6, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=1, K=50, Typ=0, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=1, K=50, Typ=1, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=1, K=50, Typ=4, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=2, K=50, Typ=0, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=2, K=50, Typ=1, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=2, K=50, Typ=4, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=4, K=50, Typ=0, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=4, K=50, Typ=4, B=[-4, 4]x[-4, 4]
  • Phase Plot, Polygamma-Funktion, m=7, K=50, Typ=0, B=[-4, 4]x[-4, 4]

Eisenstein-Reihe

  • Eisensteinreihe, k=2, c,d=-50,...,50, B=[-1, 1]x[0, 2]
  • Eisensteinreihe, k=4, c,d=-50,...,50, B=[-1, 1]x[0, 2]
  • Eisensteinreihe, k=6, c,d=-50,...,50, B=[-1, 1]x[0, 2]
  • Eisensteinreihe, k=8, c,d=-50,...,50, B=[-1, 1]x[0, 2]
  • Eisensteinreihe, k=10, c,d=-50,...,50, B=[-1, 1]x[0, 2]
  • Eisensteinreihe, k=12, c,d=-50,...,50, B=[-1, 1]x[0, 2]

Lambert-Reihe

  

vgl. auch mit Komplexe Folgen und Reihen

  • Phase Plot, Funktion 32, N=20, Typ=0, B=[-1.5, 1.5]x[-1.5,1.5]
  • Phase Plot, Funktion 32, N=20, Typ=1, B=[-1.5, 1.5]x[-1.5,1.5]
  • Phase Plot, Funktion 32, N=20, Typ=4, B=[-1.5, 1.5]x[-1.5,1.5]
  • Phase Plot, Funktion 32, N=20, Typ=6, B=[-1.5, 1.5]x[-1.5,1.5]
  • Phase Plot, Funktion 32, N=4, Typ=4, B=[-1.5, 1.5]x[-1.5,1.5]
  • Phase Plot, Funktion 32, N=6, Typ=4, B=[-1.5, 1.5]x[-1.5,1.5]


Download

Mit dem zum Download bereitstehenden Shader können Sie Phase Plots für diverse Funktionen erstellen. Der Shader ist in OpenGL programmiert und kann mit dem Tool VOC ausgeführt werden (s. dazu Verwendung der bereitgestellten Shader unter VOC - Tool zur Berechnung und Darstellung).

Im Programmcode können eingestellt werden:

  • Komplexer Teilbereich B des Definitionsbereichs D der komplexen Funktion,
  • Modell / Typ der Einfärbung (s. Grundlagen und Algorithmen),
  • Nummer der im Program implementierten Funktion f.

Darüber hinaus stehen im VOC-Editor sechs freie Parameter P1 … P6 (Typ Float) zur Verfügung, auf die sich im Programm bezogen werden kann, um z.B. den Maximalwert für einen Summenindex variabel einzustellen.


Impressum | Datenschutz | Cookie-Richtlinie | Sitemap
© Dr. Bernd Frassek • 2018 - 2024
Abmelden | Bearbeiten