2D Superformel - Teil 2
Transformation der Archimedischen Spirale
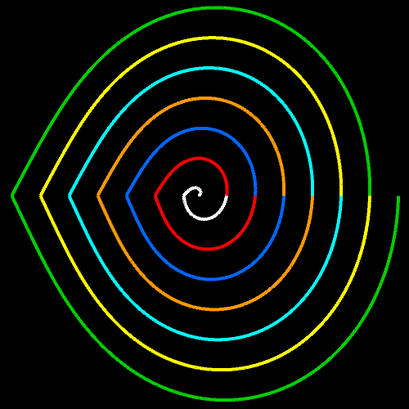
Im Fall f (φ) = c · φ mit c ∈ ℝ , c ≠ 0 wird eine Archimedische Spirale transformiert.
Für rotationssymmetrische Transformationen kann die Superformel vereinfacht werden:
mit m ∈ ℕ, p,q ∈ ℝ, q ≠ 0.
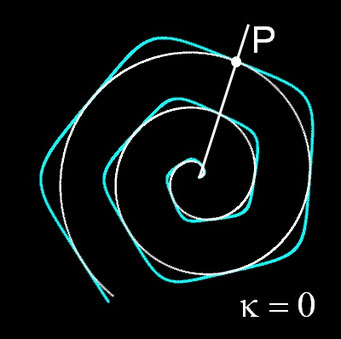
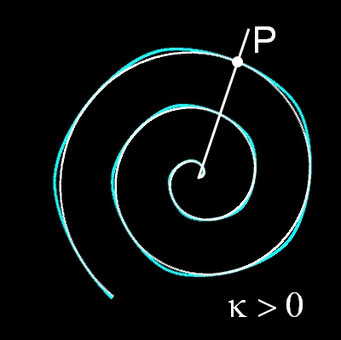
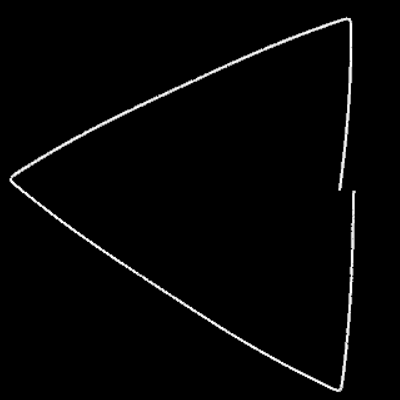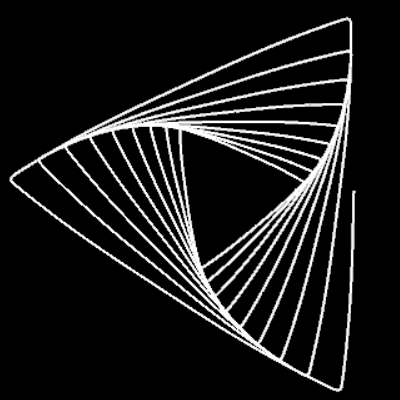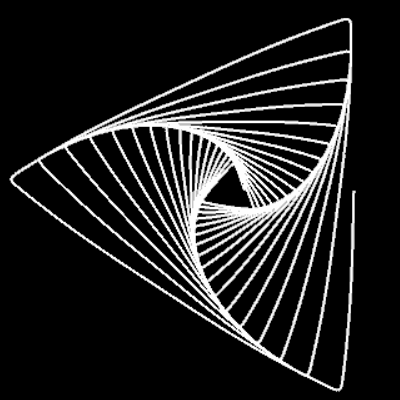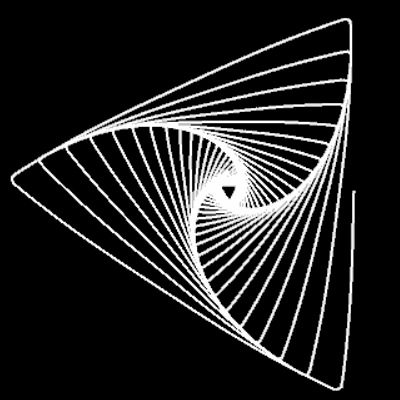
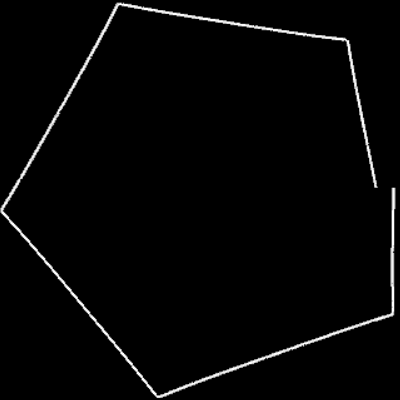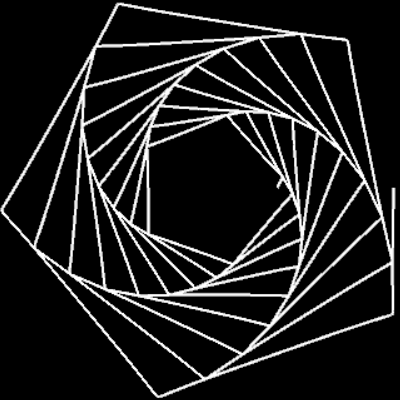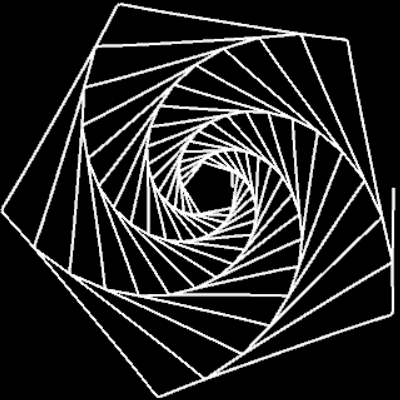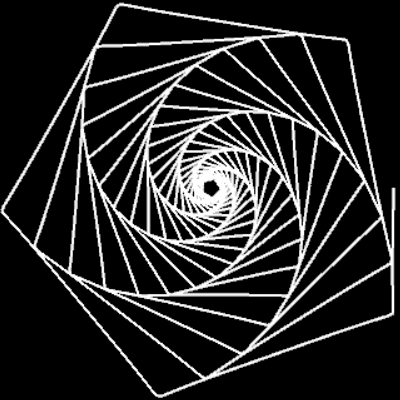
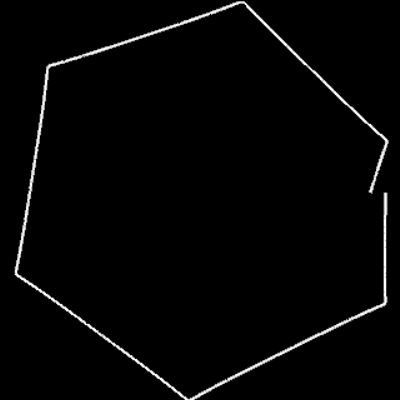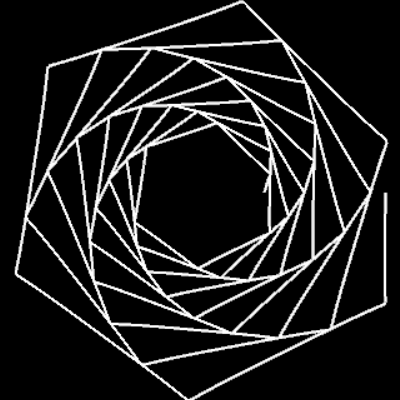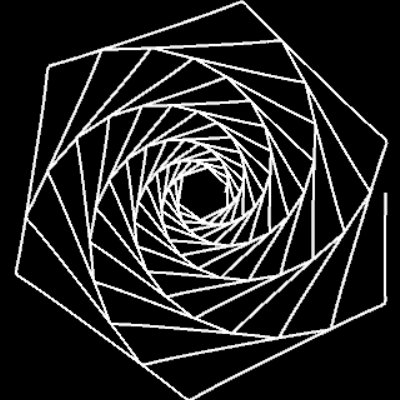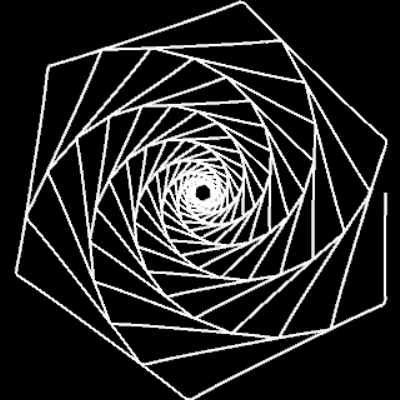
Für m = 0, p = 0, q = 1, c = 1 ergibt sich die nicht-transformierte Spirale f (φ) = c · φ. In der Grafik rechts sowie in den folgenden Galerien, die Beispiele für einige Kombinationen aus m, p und q zeigen, ist 0 ≤ φ ≤ 10 π.
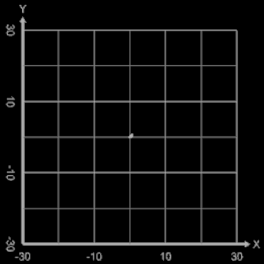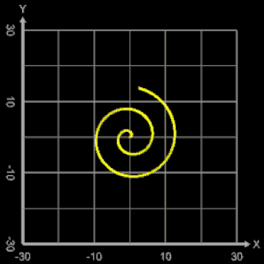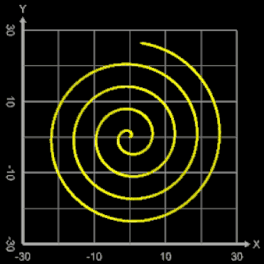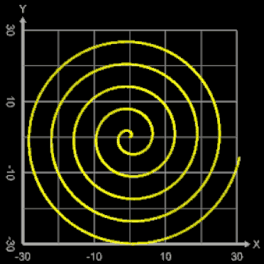
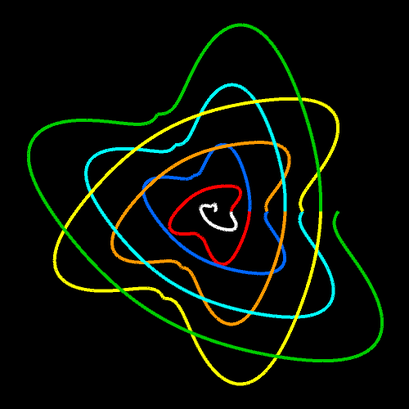
m = 1: q=1, p=0.5, 1, 3 | q=5, p=5 | q=55, p=100 | q=1, p=-1 | q=-1, p=1 | q=100, p=-100
m = 2: q=1, p=0.5, 1, 5 | q=5, p=5 | q=55, p=100 | q=1, p=-1 | q=100, p=-100 | q=-1, p=1
m = 3: q=1, p=0.5, 1, 3 | q=5, p=5 | q=55, p=100 | q=1, p=-1 | q=100, p=-100 | q=-1, p=1
m = 4: q=1, p=0.5, 1, 3 | q=5, p=5 | q=100, p=100 | q=1, p=-1 | q=100, p=-100 | q=-1, p=1
m = 5: q=1, p=0.5, 1, 3 | q=5, p=5 | q=156, p=100 | q=1, p=-1 | q=100, p=-100 | q=-1, p=1
m = 6: q=1, p=0.5, 1, 3 | q=5, p=5 | q=225, p=100 | q=1, p=-1 | q=100, p=-100 | q=-1, p=1
Betrachtet man die transformierten Spiralen, so stellt man fest, dass diese jeweils m Ecken unterschiedlichen Typs haben. In [1] untersuchte der Verfasser dies genauer und definierte die Subspirale und Superspirale, die bei der Transformation abhängig vom Parameter p entstehen:
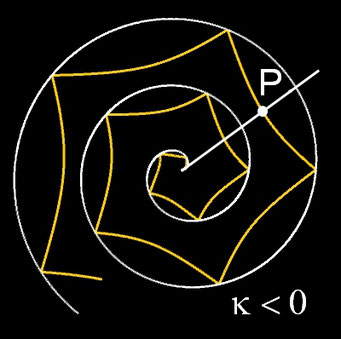
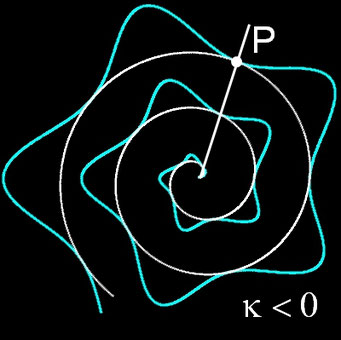
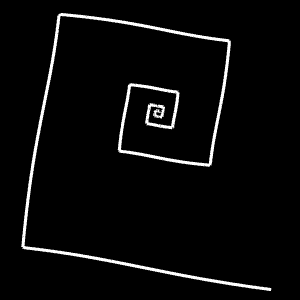
- p < 2: Es entsteht eine Subspirale, die unterhalb der Ausgangsspirale f (φ) verläuft und deren Ecken auf dieser liegen.
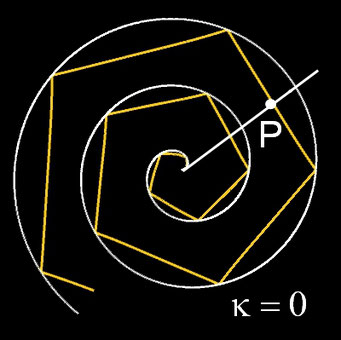
- p = 2: Transformierte und Ausgangsspirale sind identisch, da cos²(β) + sin²(β) = 1.
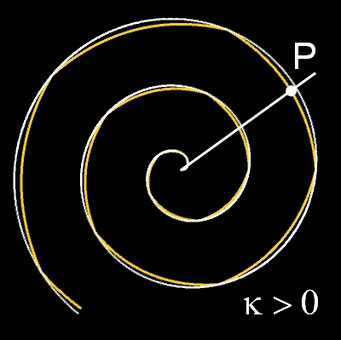
- p > 2: Es entsteht eine Superspirale, die inklusive der Ecken oberhalb von f (φ) verläuft.
Um die transformierten Spiralen zu typisieren, lege man einen Strahl, ausgehend von (0 | 0) hälftig in den Winkel zweier aufeinander folgender Ecken und betrachte die Krümmung k in den Schnittpunkten des Strahls mit der transformierten Spirale. Sowohl für die Sub- als auch die Superspirale gilt, dass k entweder kleiner, gleich oder größer als 0 ist. In der folgenden Galerie sind entsprechende Beispiele für verschiedene Wertekombinationen p|q dargestellt.
Subspirale: 1|1: k<0 1| (m/4)²p: k=0 1|8: k>0 Superspirale: 5|3: k<0 5| (m/4)²p: k=0 5|25: k>0
Für nicht-ganzzahlige Werte für m und p ≠
2 entstehen die Spiralen in der folgenden Galerie. Für jeweils
p = 1, q = 4 wurde m = 3, 3.1, ..., 3.9, 4 gewählt (von links nach rechts). Dabei wurde der Bereich für φ in 2π breite Teilintervalle [k 2π, (k+1) 2π] mit k = 0, 1, 2, ..., 7
eingeteilt und der entsprechende Spiralabschnitt für die Teilintervalle unterschiedlich eingefärbt. Die letzten vier weißen Spiralen wurden für φ = 0...20π erstellt (die gewählten Parameter erhalten Sie durch Anklicken der
Spirale).
Ersetzt man den Parameter p in der bisher verwendeten Formel wieder durch n1 und n2 wie in der ursprünglichen Superformel, so lassen sich weitere, interessante Spiralen erzeugen; einige Beispiele zeigt die folgende Galerie.
Transformation der Logarithmischen Spirale
Mit der Funktion f (φ) = a · exp (b · φ) mit a, b ∈ ℝ , a ≠ 0 wird eine Logarithmische Spirale [2] transformiert.
Für rotationssymmetrische Transformationen kann die ursprüngliche Superformel vereinfacht werden:
mit m ∈ ℕ, p,q ∈ ℝ, q ≠ 0.
Für m = 0, p = 0, q = 1, a = 1, b = 0.1 und 0 ≤ φ ≤ 10 π ergibt sich die nicht-transformierte Logarithmische Spirale in der Grafik rechts. Im Prinzip gelten die obigen Aussagen und Beispiele zu Archimedischen Spiralen auch für Logarithmische Spiralen.
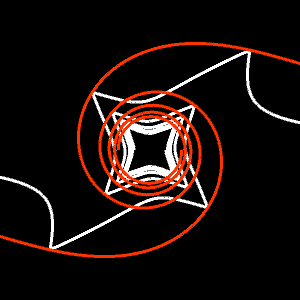
Der wesentlichen Unterschied ist der, dass bei Logarithmischen Spiralen der Abstand zwischen aufeinander folgenden Wicklungen exponentiell zunimmt, während er bei Archimedischen Spiralen konstant ist. Die folgende Galerie zeigt einige Beispiele Archimedischer Spiralen (obere Reihe) und ihrer logarithmischen Pendants (untere Reihe).
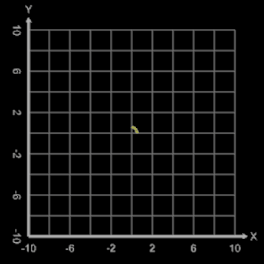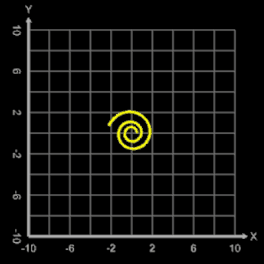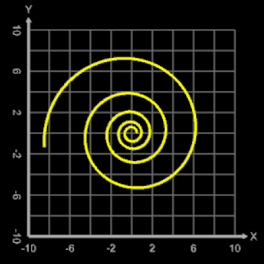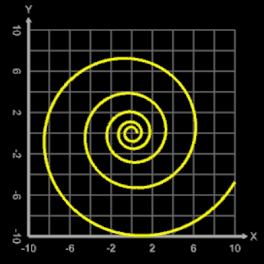
Bei einigen Werten der Parameter m, p, q erzeugen die transformierten Spiralen Kurven, die Wirbeln [3] ähneln. Diese Kurven ergeben sich auch beim Mäuseproblem, auch Käferproblem [4] genannt, bei dem n Mäuse an den Ecken eines regelmäßigen n-Ecks platziert sind. Ab einem bestimmten Zeitpunkt bewegen sich die Mäuse mit konstanter Geschwindigkeit jeweils auf die nächste Nachbarmaus zu. Die Mäuse beschreiben jeweils eine logarithmische Spirale, deren Zentrum im Zentrum des n-Ecks liegt.
Die nebenstehende Animation zeigt den Fall für n = 4 Mäuse, die sich anfangs an den Ecken eines Quadrates befinden.

Geeignete Werte für m bei festem b und p für die Transformationen einer logarithmischen Spirale, die einem Wirbel ähnelt, sind die Lösungen der Gleichung [1]
Zum Beispiel kann für die Wahl b = 0.02 und p = 100 m folgende Werte annehmen (gerundet auf 5 Nachkommastellen): 0.990904, 1.00931, 1.97514, 2.02596, 2.94811, 3.05571, 3.90679, 4.10404, 4.84562, 5.18405, 5.75107, 6.37020, 6.54821.
Die folgende Galerie zeigt als Animation die entstehenden Spiralen für b = 0.02, p = 100, -25·2π ≤ φ ≤ 0 und m = 3.05571, 4.10404, 5.18405 und 6.37020.
Hier noch ein paar weitere logarithmische Spiralen:
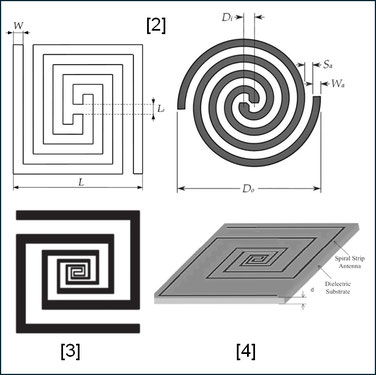
Beispiele für die technische Anwendung von Spiralen findet man im Antennenbau. Die Forderung nach Miniaturisierung der Antennen, wie z.B. im Mobilfunkbereich, führte zu planaren Spiral-Antennen, hauptsächlich basierend auf einem archimedischen oder logarithmischen Design und in diversen Konfigurationen, wie z.B. kreisförmig, rechteckig, mäanderförmig oder logarithmisch, wobei das hauptsächliche Ziel weitgehend frequenzunabhängige Antennen sind [5], [6], [7].
Zum einen lassen sich viele dieser Konfigurationen durch eine Gielis-Transformation approximieren, zum
anderen könnte die relative Einfachheit und Flexibilität der Transformation genutzt werden, um eine fortschrittliche oder neuartige
Antennenkonstruktion zu entwickeln. Die folgende Galerie zeigt einige planare Phantasie-Spiral-Antennen basierend auf Archimedischen und Logarithmischen Spiralen.
Außer der Archimedischen und Logarithmischen Spirale können natürlich auch weitere, spezielle Spiralen transformiert werden. Mit der Darstellung der Spirale in der Form
zeigen die folgenden Abbildungen Gielis-Transformationen mit a = b = n1 = n2 = 1, m = 8, n3 =0 und n für vier Spiralen (weitere Ansichten / Eigenschaften dieser Spiralen s. auch unter 3d-mathe/3d-spiralen/).
Transformation weiterer Funktionen
Um die Möglichkeiten bei der Modellierung geometrischer Formen nochmals zu erweitern, wird die Superformel weiter verallgemeinert [8]:
wobei es sich bei c (φ), f1 (φ) und f2 (φ) um stetige Funktionen handelt. Die Division durch 4 ist nicht erforderlich, da m1 und m2 entsprechend gewählt werden können. Sie wird aber weiterhin verwendet, um die ursprüngliche Form der Superformel und den Sonderfall der Lamé-Kurven für m = 4 beizubehalten.
Eine mögliche Wahl für f1 (φ) oder f2 (φ) sind Funktionen f (φ), so dass f (-π) = -π und f (π) = π gilt, wie z.B. f (φ) = 2 arcsin (φ / π) oder f (φ) = π (φ / π)2j+1 mit j = 0, 1, 2,…., die in den folgenden beiden Galerien verwendet werden.
c (φ) = 1
a = 2, b = 5
m1 = m2 = 10
n1 = 3, n2 = 3, n3 = 3
f1
(φ)
=
π (φ
/
π)k
f2 (φ) = f1 (φ)
-π ≤ φ ≤ π
k = 1, 2, 3, 5, 15
c (φ) = 2 (φ² - π²)
m1 = m2 = 19
n1 = -9, n2 = 14, n3 = 11
f1
(φ)
=
2 arcsin (φ
/
π)
-π ≤ φ ≤ π
f2 (φ) = f1 (φ), a = 2, b = 1
f2 (φ) = φ (φ / π)3,
(a, b) = (1, 1), (1, 5)
Um geschlossene Kurven zu erhalten ist es hinreichend, die Funktionen so zu wählen, dass f (-π) = f (π) gilt. Hierfür können z.B. gewählt werden f (φ) = sin (k φ) j oder f (φ) = cos (k φ) j mit k, j ∈ ℕ. Beispiele hierzu zeigt die folgende Galerie.
c (φ) = 1
a = 2, b = 7
m1 = m2 = 30
n2 = 3, n3 = 3
f1
(φ)
=
3 sin3
(2 |
φ -
π/3 |)
f2 (φ) = 2 cos2 (3 (φ + π/2)
-π ≤ φ ≤ π
n1 = 5, 31, -5, -31
Weiterhin können trigonometrische Polynome der Form f (φ) = A sin (φ) + B cos (2 φ) verwendet werden, die in π und -π verschwinden. Die folgende Galerie zeigt hierzu einige Beispiele.
c (φ) = 1
a = 2, b = 173
m1 = m2 = 4
n1 = -2, n2 = 2, n3 = 2
f1
(φ)
=
3 sin
(k φ)
+ 5 cos (2
φ)
f2 (φ) = 3 cos (φ) + 5 sin (2 φ)
-π ≤ φ ≤ π
k = 1, 3, 4
Darüber hinaus gibt es unzählige weitere Möglichkeiten; ein paar enthält die folgende Galerie, wobei der Definitionsbereich variiert wurde.
c (φ) = 2 (φ² - π²)
a = 12, b = 3
m1 = m2 = 3
n1 = -3, n2 = 2, n3 = 3
f1
(φ)
=
3 |
φ
|
f2 (φ) = sin (2 φ) + 3 cos (φ)
φ ∈
[-π,
π], [-2π,
2π],
[-3π,
3π]
Abschließend sei noch erwähnt, dass während die ursprüngliche Gleichung der Superformel eindeutig in der Lage ist, eine Reihe unterschiedlicher biologischer Formen mit unterschiedlichen Symmetrien zu beschreiben, es nach Ansicht von Experten eher unwahrscheinlich erscheint, dass diese Formel eine besonders grundlegende biologische Bedeutung hat [9] und wahrscheinlich keine Erkenntnisse darüber vermittelt, wie diese Formen in der Natur tatsächlich entstehen [10], welche Art von physikalischer Dynamik hinter der Formel steckt. Allerdings habe laut Gielis die bloße mathematische Beschreibung eines biologischen Endprodukts schon oft Hinweise auf den zugrundeliegenden Mechanismus offenbart.
Obschon die Anzahl der freien Parameter in der Superformel sechs beträgt, wird sie auch als Vorfaktor für andere Polarkurven (z. B. die logarithmische Spirale, die Rosenkurve usw., s.o.) verwendet, sodass die Anzahl der Parameter in der Gleichung effektiv größer ist.
Natürlich kann jede Formel mit einer großen Anzahl freier Parameter einen sehr großen Parameterraum beschreiben. Um diese Tatsache zu betonen, wird hierzu manchmal auf das Bonmot von John von Neumann zurückgegriffen, der 1950 die erste computerbasierte Wettervorhersage erstellte und angesichts der zahlreichen Parameter für die Simulation gesagt hat: "With four parameters I can fit an elephant, and with five I can make him wiggle his trunk" [11]).

Quelle: wdr.de
Quellenverweise
[1] L.
Spíchal (2020) Gielisova transformace logaritmické spirály, Pokroky matematiky, fyziky a
astronomie, Vol. 65 (2020), No. 2, 76–89
[2] https://mathworld.wolfram.com/LogarithmicSpiral.html
[3] https://mathworld.wolfram.com/Whirl.html
[4] https://en.wikipedia.org/wiki/Mice_problem
[5] A. A. Hasan et al. (2023) On Modeling Antennas Using MoM-Based Algorithms: Wire-Grid versus
Surface Triangulation, Algorithms 2023, 16, 200. https://doi.org/10.3390/a16040200
[6] U. Saynak, A. Kustepeli (2009) Novel Square Spiral Antennas for Broadband Applications,
Frequenz -Berlin- 63 (1-2): 14-19,
DOI:10.1515/FREQ.2009.63.1-2.14
[7] U. Saynak, A. Kustepeli (2007) A Novel Square-Spiral Strip Antenna,
2nd International ITG Conference on Antennas 2007, DOI:10.1109/INICA.2007.4353961
[8] J. Gielis, P. Natalini, P. E. Ricci (2019) A Note About Generalized Forms of the Gielis Formula,
Modeling in Mathematics, Conference Paper, S. 108, DOI: 10.2991/978-94-6239-261-8_8
[9] https://mathworld.wolfram.com/Superellipse.html
[11] https://blog.math.rptu.de/index.php/2024/01/19/der-von-neumannsche-elefant/