2D Superformel - Teil 1
Der belgische Wissenschaftler Johan Gielis spezialisierte sich auf die Biotechnologie und beschäftigt sich insbesondere mit der mathematischen Modellierung von Pflanzen. Im Jahr 1997 veröffentlichte er seine Superformel und ließ diese später sogar patentieren [1].
Ausgangspunkt für die Superformel war die Gleichung der Lamé'schen Kurve
mit der sich verschiedene Kurventypen, wie z.B. Asteroiden (n=2/3), Parallelogramme (n=1), Kreise und Ellipsen (n=2) und Superellipsen erzeugen lassen (s. auch unter Piet Heins Superei). Die Gleichung lässt sich auch in Polarkoordinaten ausdrücken:
Superformel: Transformation des Kreises
Gielis verallgemeinerte diese Gleichung, indem er den gemeinsamen Exponent n durch drei unabhängige Exponenten n1, n2, n3 ersetzte und einen weiteren Parameter ¼ m im Argument der trigonometrischen Funktionen hinzufügte, der speziellere Rotationssymmetrien um den Koordinatensystemursprung ermöglicht als diejenigen, die sich auf die vier Quadranten des kartesischen Koordinatensystems beziehen:
In gewissem Sinne können die durch diese Gleichung erzeugten Kurven als Transformation des Einheitskreises (r = 1, Mittelpunkt in (0 | 0)) gemäß der Parameter a, b, m, n1, n2, n3 interpretiert werden. In entsprechender Literatur ist daher oft von der Gielis-Transformation anstelle der Superformel die Rede.
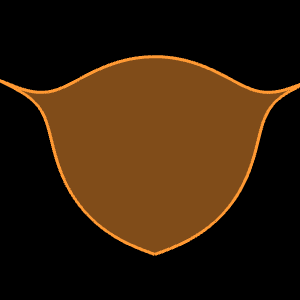
Für die erzeugte Kurve bestimmen m die Symmetrie, n1, n2 und n3 die Form, a und b die Ausdehnung (Größe der Halbachsen). Mit der Superformel lässt sich eine Vielzahl von (organisch wirkenden) Formen unterschiedlicher Symmetrie durch Änderung nur weniger Parameter erzeugen.
Die folgende Bildergalerie zeigt einige Figuren, die ich mit Graphing Calculator 3D erzeugt habe. Hierbei wurde die Möglichkeit des Programms genutzt, auch Ungleichungen darstellen zu können, so dass die Fläche unter der Kurve farblich gefüllt werden kann.
Für ein Objekt sind dazu zwei Ungleichungen für den oberen und unteren Anteil der Figur (s. Bild rechts) erforderlich:
█ r < Superformel mit 0 ≤ φ ≤ π 0 ≤ r ≤ 1
█ r > Superformel mit -π ≤ φ ≤ 0 -1 ≤ r ≤ 0
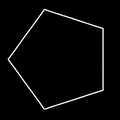
Mit der Superformel lassen sich auch Näherungen regelmäßiger Vielecke sowie Rauten und Rechtecke erzeugen:
Kreis
m = 0
n1,2,3 = 1
Dreieck
m = 3
n1 = 313
n2,3 = 602
Fünfeck
m = 5
n1 = 1000
n2,3 = 620
Sechseck
m = 6
n1 = 1000
n2,3 = 390
Siebeneck
m = 7
n1 = 1000
n2,3 = 320
Achteck
m = 8
n1 = 1000
n2,3 = 500
Ist m nicht ganzzahlig, so schließt sich die entstehende Figur nicht für φ ≤ 2π, sondern erst für φ ≤ k · 2π. Dazu hier ein paar Beispiele mit b = 1, n1,2,3 = 1:
a = 1, m = 3/2
k = 2
a = 1, m = 3/2
k = 4
a = 1, m = 2/3
k = 3
a = 1, m = 5/3
k = 4
a = 2, m = 5/3
k = 6
a = 1, m = 11/2
k = 2
Ersetzt man den Parameter m durch zwei verschiedene Parameter m1 und m2,
so erhält man weitere Formen:
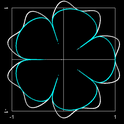
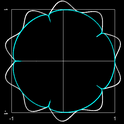
Transformation der Grandi Rosette zur Modellierung von Blüten
Anstelle des Einheitskreises können grundsätzlich auch alle planaren Kurven, die durch die polare Gleichung r = f (φ) definiert sind und f eine positive reelle Funktion ist, transformiert werden:
Mit f (φ) = c mit c ∈ ℝ , c ≠ 0 liegt der bisher betrachtete Fall der Transformation eines Kreises mit Radius c (c = 1: Einheitskreis) vor.
Um nun Blüten zu modellieren, bietet es sich an, für die Funktion f eine Grandi Rosenkurve (Rosette) zu verwenden, d.h. f (φ) = cos (m ∙ φ) (s. Rosenkurven). Damit die Anzahl der Blütenblätter identisch mit m ist, wird die Superformel wie folgt angepasst [19, S. 67]:
Folgende Eigenschaften dieser Gleichung für a, b = 1 erleichtern einem etwas die Suche nach geeigneten Parameterwerten bei der Modellierung einer Blüte (s. dazu folgende Grafiken mit cyan-farbiger Grandi Rosette und Blütenkurve in weiß):
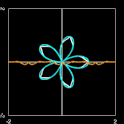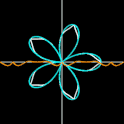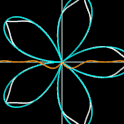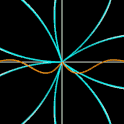
- Gilt n2,3 < 2, so ist die Grandi Rosette eine Einhüllende der erzeugten Blütenkurve (Grafik 1).
- Im Fall n2,3 = 2 sind Grandi Rosette und erzeugte Blütenkurve identisch, da cos2(x) + sin2(x) = 1.
- Gilt n2 > 2 und / oder n3 > 2, liegt die Blütenkurve teilweise außerhalb der Grandi Rosette (Grafik 2). Die Differenz der Blütenkurve und der Grandi Rosette zeigt die orangene Kurve in Grafik 3.
- Mit wachsendem n4 nähert sich die Grandi Rosette dem Einheitskreis, da die n4-te Wurzel aus | x | gegen 1 läuft (Grafik 4, 5).
Grafik 1
n2 = 1
n3 = 1
n4 = 1
Grafik 2
n2 = 3 > 2
n3 = 2
n4 = 1
Grafik 3
n2 = 3 > 2
n3 = 1
n4 = 1
Grafik 4
n2 = 3
n3 = 2
n4 = 10
Grafik 5
n2 = 3
n3 = 2
n4 = 50
Um auch Blütenblätter zu modellieren, die eine zusätzliche Rotationssymmetrie aufweisen, wird die bisherige Superformel um die weiteren Parameter δ1 und δ2 erweitert [19, S. 87]:
Somit lassen sich z.B. auch die Blüten des Borretsch, Kleinen Immergrüns und Ziertabaks modellieren
(s. nächste Galerie). In der folgenden Animation mit
δ1 =
δ2 durchlaufen diese die Werte 0 bis 1.25.
Für einige Blüten habe ich mich an einer Modellierung versucht und die Ergebnisse in der folgenden Galerie zusammengestellt.
Acker-Hornkraut [3]
Phlox paniculata [4]
Chili [5]
Gewöhnliche Haselwurz [6]
Butterblume [7]
japanischer Blumen-Hartriegel [8]
Campanula carpatica [9]
Porzellanblume [10]
Borretsch [10]
Sauerklee [11]
Kapuzinerkresse [12]
Schwarzäugige Susanne [13]
Sternanis [14]
Kleines Immergrün [15]
Caralluma frerei [16]
Tradescantia fluminensis [17]
Ziertabak [18]
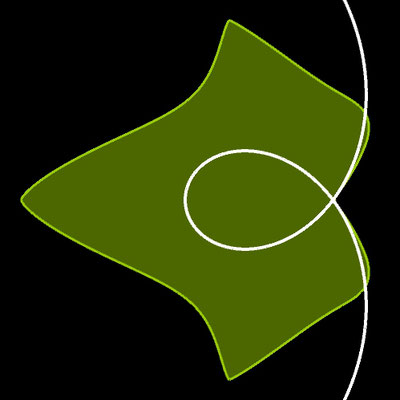
Transformation der Kardioide zur Modellierung von Blättern
Auch bei den Blättern von Pflanzen gibt es eine große Formenvielfalt. Um einige Pflanzenblätter besser modellieren zu können, kann die bei den Blütenblättern verwendete Rosenkurve f (φ) = cos (m · φ/2) durch eine geeignetere Kurve ersetzt werden, wie z.B. durch eine Kardioide [19, S. 91]:
f (φ) = c (1 - cos (d φ) ) 1/n4
(s. auch unter Herzkurven / Die Kardioide. Bei den folgenden Beispielen zu Pflanzenblättern zeigt jeweils ein drittes Bild die verwendete Kardioide im Zusammenhang mit dem Ergebnis.
Tatarischer Buchweizen [20]
Sauerampfer [21]
Hedera helix Sagittifolia [22]
Winterlinde [23]
Hedera helix Glacier [24]
Hinweis:
Da die weiteren Kapitel zur Thematik "Superformel"
- Transformation der Archimedischen Spirale
- Transformation der Logarithmischen Spirale
- Anwendungen im Antennen-Design
- Transformation weiterer Spiraltypen
- Transformation weiterer Funktionen
hier die maximale Anzahl an Objekten pro Seite überschreiten würde, finden Sie diese auf der Seite
2D Superformel - 2.
Quellenverweise
[1] Method and Apparatus for Synthesizing Patterns (Patentschrift, PDF, 3.1 MB)
[2] Mishra, Sudhanshu K. (2006) Some Experiments on Fitting of Gielis Curves by Simulated Annealing
and Particle Swarm Methods of Global Optimization, Dept. of Economics, NEHU, Shillong (India),
(July 3, 2006), http://dx.doi.org/10.2139/ssrn.913667
[3] https://de.wikipedia.org/wiki/Acker-Hornkraut
[4] https://www.teuffenbach.eu/de-at/artikel/1596/phlox-paniculata-the-king
[6] https://de.wikipedia.org/wiki/Gew%C3%B6hnliche_Haselwurz
[7] https://www.fotocommunity.de/photo/butterblume-mi00ro/41101086
[8] https://www.gaertnereibarth.de/de-de/webshop/artikel/256/cornus-kousa-chinensis-milky-way
[9] https://shop.trachtpflanzen24.de/product_info.php?info=p342_saatgut-karpaten-glockenblume
[10] https://www.mein-schoener-garten.de
[11] https://mein-kraeuterkeller.de/klee-arten
[12] https://www.energieleben.at/wp-content/uploads/2012/04/bluete.jpg
[13] https://www.gaertnereibarth.de/de-de/webshop/artikel/20331/schwarzaeugige-susanne...
[14] https://www.kochschule.de/kochwissen/sternanis
[15] https://backend.mein-schoener-garten.de/sites/default/files/chameleon/images/189d885898c974ef.jpg
[16] https://www.ipernity.com/doc/picture_taker/31491821
[17] https://upload.wikimedia.org/wikipedia/commons/0/05/Tradescantia_fluminensis_Flower_1.jpg
[18] https://www.gartenratgeber.net/pflanzen/ziertabak.html
[19] J. Gielis (2017) The Geometrical Beauty of Plants, Paris : Atlantis Press , ISBN 978-94-6239-150-5,
978-94-6239-151-2, https://doi.org/10.2991/978-94-6239-151-2
[20] https://agrobaseapp.com/united-states/weed/tartary-buckwheat-1
[21] https://www.pflanzen-koelle.de/sauerampfer-koelle-bio...
[23] https://www.tierfreund.de/linde/
[24] https://www.bauer-baumschulen.ch/de-ch/pflanzenshop/kletterpflanzen/hedera-helix-glacier
Download
